降低零阶方法对维度的依赖
零阶方法简介
简单地说,零阶方法是通过访问函数值或者计算函数值的差值来得到下降方向,以此来优化目标函数。
此篇考虑一个 \(L\) 光滑且无约束的函数 \(f\),
根据Yurri Nesterov等人提出的高斯光滑技巧,我们可以通过
来获得随机下降方向。其中向量\(\xi \sim \mathcal{N}(0, I_d)\),\(\rho\)是一个比较小的光滑系数。
不难看出,上式子基本是按照定义来近似方向导数的。当光滑系数 \(\rho\to 0\),那么我们就可以得到
也就是函数 \(f\) 在 \(x\) 点沿着 \(\xi\) 方向的方向导数。
根据Yurri Nesterov等人的结论,沿着获得的 \(\tilde{\nabla}_{\rho} f(x)\) 进行梯度下降,
- 对于光滑且强凸的函数 \(f\), 复杂度为\(\mathcal{O}(d\kappa\log(\frac{1}{\epsilon}))\);
- 对于光滑且凸的函数 \(f\),复杂度为\(\mathcal{O}(\frac{dL}{\epsilon})\)。
相比于梯度下降法的复杂度,上面的结果都多出来一个\(d\)。对于零阶优化的一个共识就是,由于其只近似一个方向的方向导数,其复杂度是与维度有关的。
降低维度依赖
从上面的结果可以看出,如果当维度比较大的时候,比如对于13B的一个大模型而言,其维度贡献的复杂度就要 \(\mathcal{O}(10^{10})\)。这个复杂度基本是处理不了的,但是Malladi他们实验证明零阶方法是可以微调的,是可以在这种情况下work的。这样的实验结果是跟上面的理论是有一定出入的。
之前研究人员为了降低零阶方法的复杂度与维度的关系,提出过利用 \(l_1\) 范数等方法,将复杂度降低到 \(s\log(d)\) 这种程度。Yue等人对 \(vanilla\) 的零阶方法对于维度的依赖进行了分析。
在他们的分析中,他们引入
其中\(\sigma_{i}\)表示按照降序排列的第\(i\)个奇异值。
同时通过广义的 \(mahalanobis\) 范数,\(\Vert \cdot \Vert_{\nabla^2 f(x)}\)通过如上定义,他们将对维度 \(d\) 的依赖转化为对 \({\rm{ED}}_\alpha\)的依赖。
这样转化的一个好处是,通常 \(Hessian\) 矩阵的奇异值除了一些极个别的比较大之外,其他的都很小。所以奇异值的加和也远小于维度和 \(L\) 的乘积,即 \({\rm{ED}}_{\alpha} \ll dL\)。
二次函数的收敛性分析
下面,我们假定 \(f\) 满足如下的形式:
同时假设获得的函数值满足
即控制了函数值的噪音范围。定义带噪音的方向导数估计,
在建立收敛性分析之前,先给出如下引理:
即控制实际的下降方向导数 \(\tilde{\nabla}_{\rho}\tilde{f}_{\delta}(x)\) 和真实的方向导数 \(\tilde{\nabla} f(x)\) 的差距。
强凸且光滑
在强凸条件下,根据光滑的条件,我们可以得到
通过前面的引理,重新整理后可以得到
利用强凸的条件,我们可以消除掉 \(\Vert \nabla f(x)\Vert^2\)项,
带入重新整理后可得
即复杂度为\(\mathcal{O}(\frac{\text{ED}_1}{\mu}\log(\frac{1}{\epsilon}))\)。
凸且光滑
利用凸函数的性质,
再结合柯西施瓦茨不等式,并带入到上面得到的结果
我们可以得到
即最终的复杂度为 \(\mathcal{O}(\frac{\text{ED}_1}{\epsilon})\)。
对于利用类似
heavy ball的加速方法和对于一般光滑函数的复杂度,这里略去。
参考
- Nesterov, Y., & Spokoiny, V. (2017). Random gradient-free minimization of convex functions. Foundations of Computational Mathematics, 17, 527-566.
- Yue, P., Yang, L., Fang, C., & Lin, Z. (2023, July). Zeroth-order optimization with weak dimension dependency. In The Thirty Sixth Annual Conference on Learning Theory (pp. 4429-4472). PMLR.
- Malladi, S., Gao, T., Nichani, E., Damian, A., Lee, J. D., Chen, D., & Arora, S. (2023). Fine-Tuning Language Models with Just Forward Passes. arXiv preprint arXiv:2305.17333.

 降低零阶方法对维度的依赖
降低零阶方法对维度的依赖
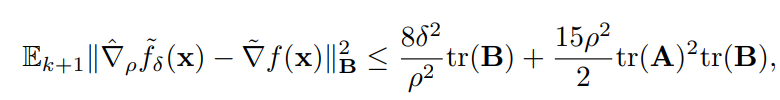
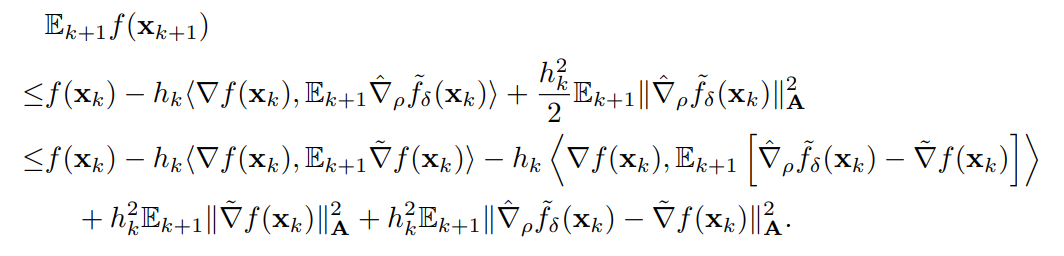
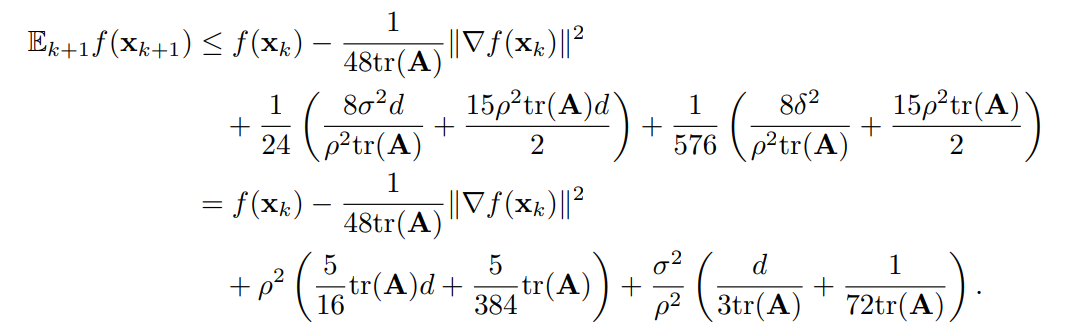
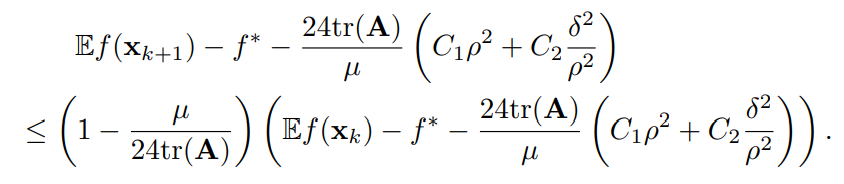
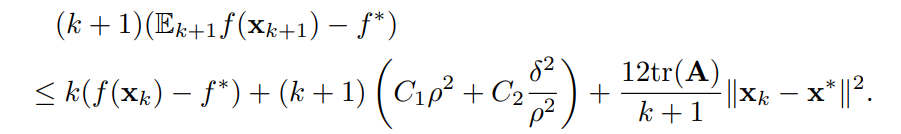

 浙公网安备 33010602011771号
浙公网安备 33010602011771号