刷题杂记 Pt.6

wqs 二分

reference：1、

1. 概述

wqs 二分主要被用来解决一种背包问题，其形式大概为：\(n\) 个物品，要求 恰好 选 \(m\) 次（一次不一定只能选一个），然后选一次时会有一个比较神秘的代价计算函数，求最大/小总代价。

辨认这类题目的方法：

  1. 题目中要求恰好选 \(m\) 次，但是可以发现在没有次数选择限制时非常容易求解。

  2. 如果令 \((i, f[i])\) 表示恰好选 \(i\) 个时的最优代价为 \(f[i]\)，那么这些点在二维坐标图上连起来可以形成一个凸包（可能是上凸壳也可以是下凸壳，下面以上凸壳为例）。

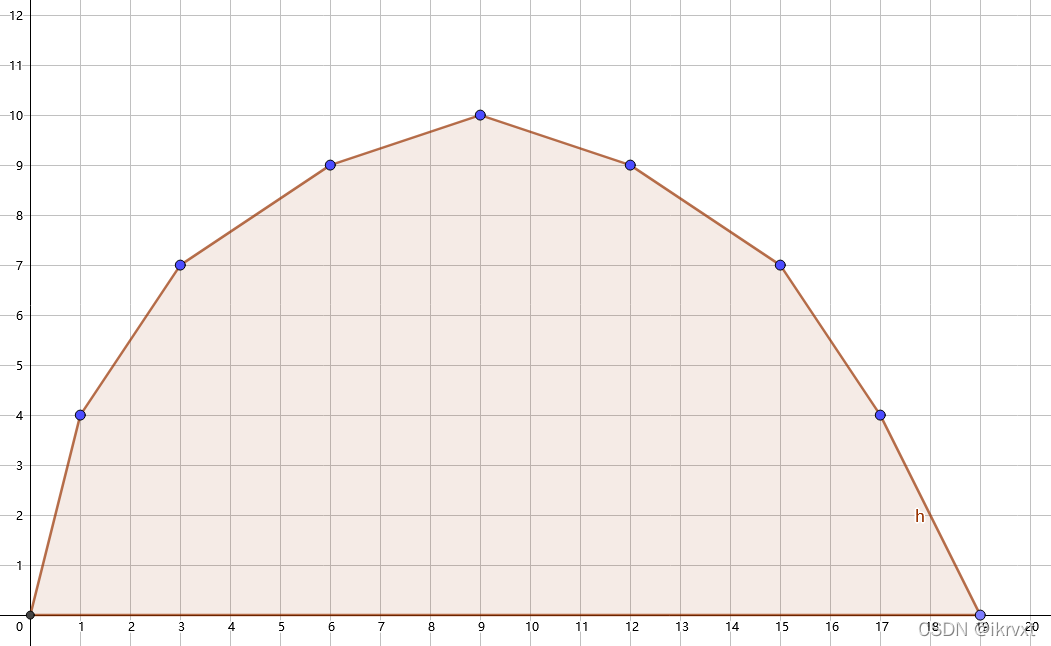
    image

    后文会教一些严谨证明凸性的方法。当然，考场上为了节省时间，你可以直接打表猜结论。

2. 算法流程

然后让我们来讲解该怎么做吧。。。

显然我们需要求解 \((m, f[m])\) 的纵坐标，但直接做很困难。

联系斜率优化，容易（？）想到用直线去“切”这个凸包。

我们先研究用一个固定斜率去切凸包时会发生什么。可以发现，我们相当于在上下平移这条直线，而在与某个或某些点相切时，有 截距 的最大化。

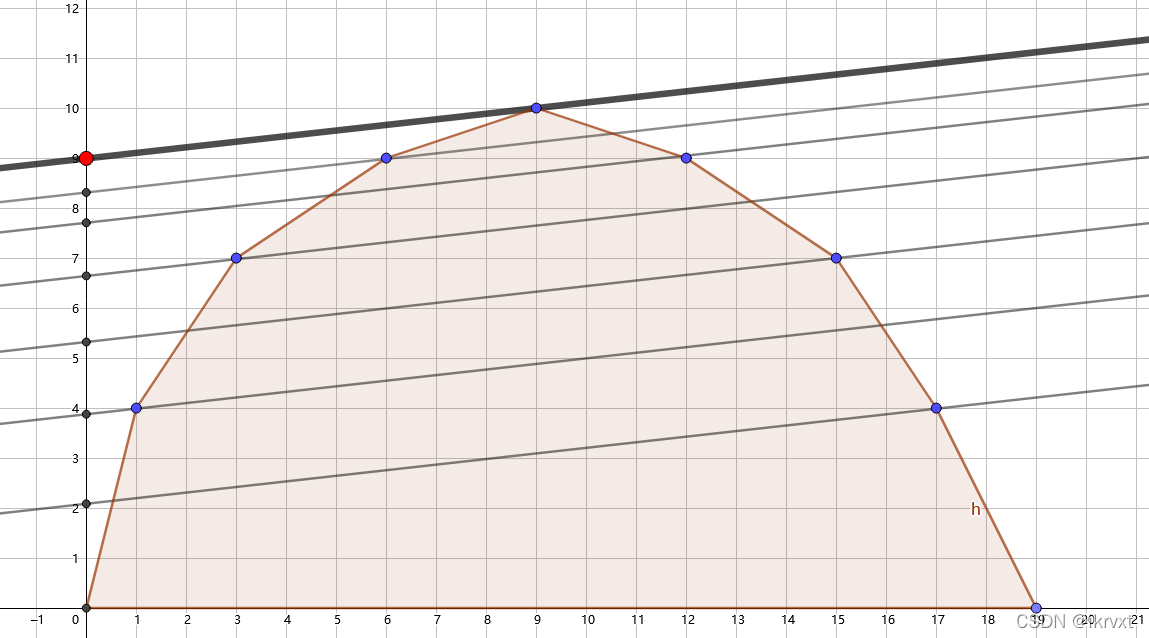
image

令截距为 \(b\)，直线斜率为 \(k\)，截距最大时相切的点的横坐标为 \(x\)。容易发现，\(b = f[x]-kx\)。

神奇的就来了——可以发现，如果我们在 DP 过程中，将每次选物品的贡献减去 \(k\)，我们就可以通过一个不限制选择次数的 DP 得到 \(b\) 和 \(x\)，进而得到 \(f[x]\)。

那么，我们只要找到一个合适的 \(k\)，使得 \(x = m\) 就可以了！不过应该怎么才能找到这个 \(k\) 呢？

可以证明，\(f[x]-f[x-1] \le k \le f[x+1]-f[x]\)。又由于它是个凸包，\(f[x]-f[x-1]\) 满足单调性。

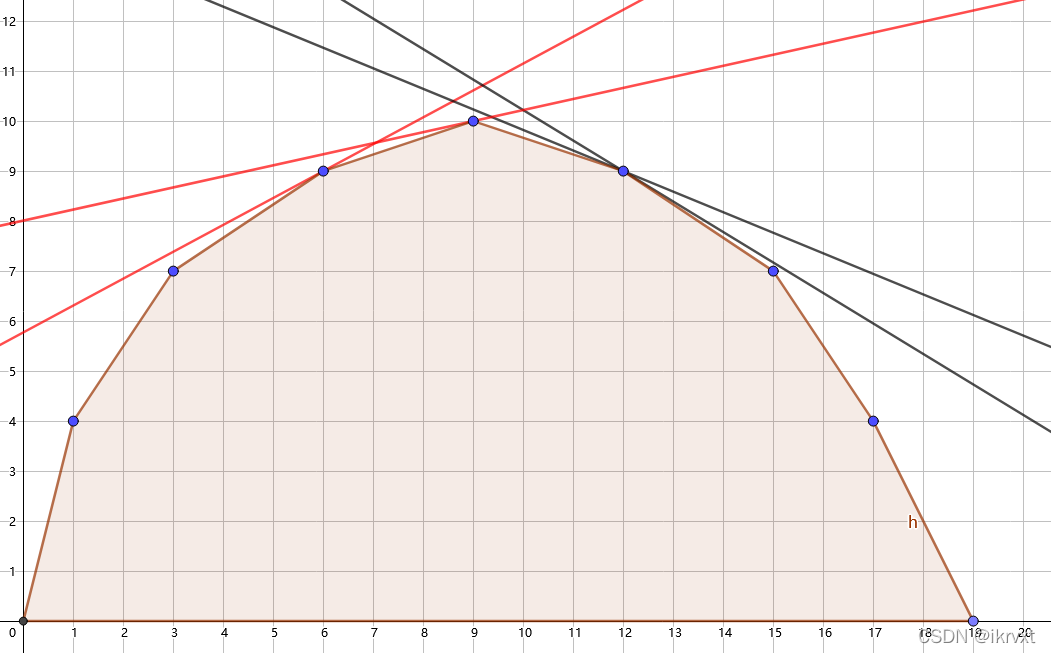
image

所以，我们可以对 \(k\) 进行二分，每次算出对应的 \(x\)，直到 \(x = m\) 即可！

不过事实上我们不一定能取到 \(x = m\)。因为可能发生像下图一样，直线斜率恰好是凸包上一条边的情况，这时一个斜率可能对应多个 \(x\)。

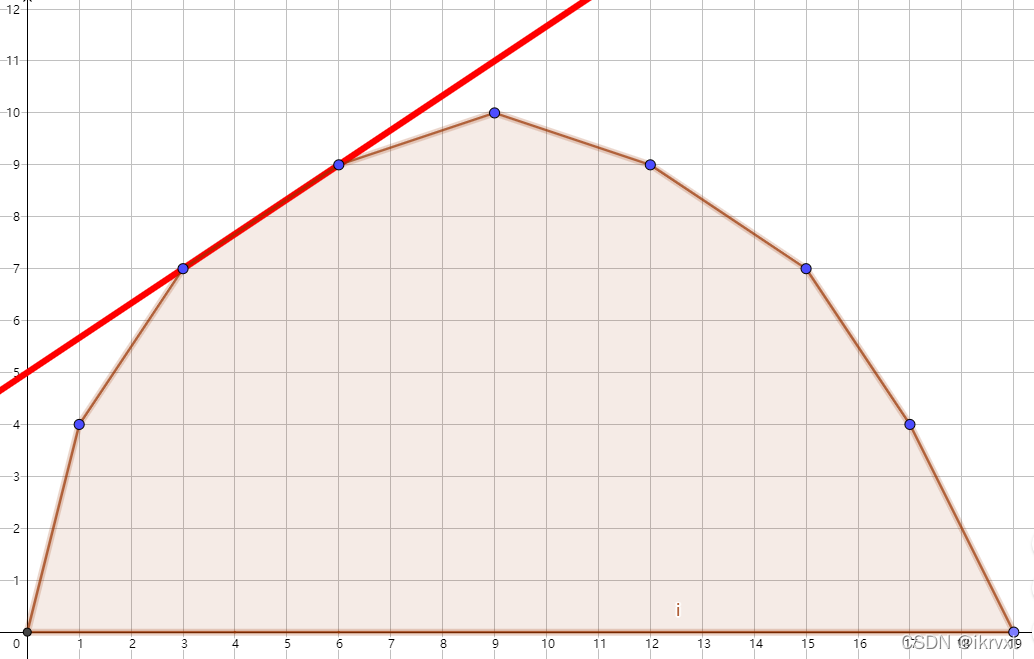
image

但这实际也不影响我们求出答案。因为显然，我们可以通过二分求得该斜率所对应的 \(x_{\min}\) 或 \(x_{\max}\)，而这两者所对应的 \(b\) 和 \(m\) 所对应的 \(b\) 都是相同的，我们依旧可以得到 \(f[m] = b + km\)。

求 \(x_{\min}\) 或 \(x_{\max}\) 都是可以的。不过求二者的方法在二分和内层 DP 的细节上稍有区别，在这里我们进行辨析：

  • \(x_{\min}\)：内层 DP 中，我们需要求出在使得总价值最优的情况下选择的最少次数；外层二分中，我们需要求出使得 \(x_{\min} \le m\) 的最后一个 \(k\)。（为什么我这里不说最大 / 最小？因为可能是上凸壳也可能是下凸壳，这会使 \(k\) 的单调性改变。）

  • \(x_{\max}\)：内层 DP 中，我们需要求出在使得总价值最优的情况下选择的最大次数；外层二分中，我们需要求出使得 \(x_{\max} \ge m\) 的第一个 \(k\)。

3. 证明凸性的一些方法

首先你需要学习 四边形不等式。

对于区间分拆问题（形如 \(g[k][i] = \min_{0 \le j < i} g[k-1][j] + w(j, i)\) 的转移方程），若 \(w\) 满足四边形不等式，则 \(f[k]\) 为上凸包；若 \(w\) 满足反四边形不等式，则 \(f[k]\) 为下凸包。

我懒得证，请看 OIwiki。

4. 题目

  • CF958E2 Guard Duty (medium)

    wqs 二分最简单的题。

    凸性很显然：每次多选一定选最小的物品。

    然后 DP 也裸得不能再裸了。

  • P4983 忘情

    忘情是二分 + 斜率优化 DP。

    凸性使用四边形不等式容易证明。

    值得注意的是，一般情况下斜率优化 DP 并不能维护那种“在最优化一个变量的前提下，最优化另一个变量”的 DP。因此这里我们使用了一个贪心：由于每个位置的贡献一定单调不降，那么我们只需要尽量找更前面/更后面的点作为决策点，就可以得到选择次数的最小化/最大化。

  • P5308 [COCI 2018/2019 #4] Akvizna

    凸性使用四边形不等式容易证明。剩下的部分也可以使用斜率优化解决。

    值得注意的是，以后见到 DP 方程中存在 \(j/k\) 的项时也可以考虑使用斜率优化。

抽象代数基础知识

在数学中，群（group）是由一个集合 \(G\)，以及一个在 \(G\) 所有元素上进行的二元运算 \(\cdot\)，符合「群公理」的代数结构，记作 \((G, \cdot)\)。

群公理：

  1. 满足封闭性。

  2. 具有结合律。

  3. 存在单位元。（\(a \cdot e = e \cdot a = a\)）

  4. 存在逆元。（\(a \cdot a^{-1} = a^{-1} \cdot a = e\)）

群性质：

  • 单位元 \(e\) 唯一。

    证明：使用反证法。若 \(e' \ne e\) 也为单位元，则 \(e \cdot e' = e\) 与 \(e \cdot e' = e'\) 矛盾。

  • 消去律：\(c \cdot a = c \cdot b \Leftrightarrow a = b\)。（右乘同理。）

    使用逆元易证。

  • 对于任意元素，其逆元唯一，且不存在仅为其左逆元、右逆元的元素。

    证明：若 \(b, c\) 皆为 \(a\) 逆元，则 \(a \cdot b = a \cdot c = e\)，根据消去律，\(b = c\)。

有关群的结构：

  • 半群：若满足封闭性、结合律，则称其为半群。

  • 幺半群：如果满足封闭性、结合律、并存在单位元，则称其为幺半群。

  • Abel 群：如果一个群还满足交换律，则称其为 Abel 群 / 交换群。

环（ring）是由一个集合 \(R\)，以及两个在 \(R\) 所有元素上进行的二元运算 \(+, \cdot\)，符合环公理的代数结构，记作 \((R, +, \cdot)\)。

环公理：

  1. \((R, +)\) 构成 Abel 群（其单位元记作 \(0\)，称作零元）。

  2. \((R, \cdot)\) 构成半群（如果存在单位元则记作 \(1\)，称作幺元）。

  3. 分配律：成立 \(c\cdot(a+b)=c\cdot a+c\cdot b\) 和 \((a+b)\cdot c=a\cdot c+b\cdot c\)。

环相关定义 & 其性质：

  • 引理：\(0 \cdot a = a \cdot 0 = 0\)。

    证明：\(b \cdot a = (0+b) \cdot a = 0 \cdot a + b \cdot a\)，消去 \(b \cdot a\) 后可得 \(0 = 0 \cdot a\)。\(a \cdot 0\) 同理。

  • 零因子：若非零元素 \(a\) 满足存在一个非零元素 \(b\) 使得 \(a \cdot b = 0\)，则 \(a\) 为一个零因子。

  • 可逆元（单位）：若某元素存在逆元则称其为可逆元。（当然，前提是存在幺元。）

  • 引理：零因子一定不为可逆元，可逆元一定不为零因子。

    证明：考虑反证法。假设存在一个元素 \(a\) 既为零因子又为可逆元，设 \(a \cdot b = 0 (b \ne 0), a \cdot c = 1\)，则 \(a \cdot (b+c) = 1\)，由于逆元的唯一性，所以 \(b+c = c \Rightarrow b = 0\)，矛盾。

    注意：可能存在非零元素既不为可逆元，也不为零因子。

有关环的结构：

  • 零环：\((\{0\}, +, \cdot)\)。（唯一一个零元和幺元相等的环。）

  • 幺环：如果含有幺元，则称其为幺环。

  • 除环：对于非零幺环，如果对于所有非 \(0\) 元素都存在乘法逆元，则称其为除环。

  • 交换环：如果乘法满足交换律，则称其为交换环。

  • 整环：若其为不为零环、为交换环、存在幺元、无零因子，则称其为整环。（即 \((R \setminus \{0\})\) 为交换幺半群。）

    整环消去律：\(a \cdot c = b \cdot c \Leftrightarrow a = b (c \ne 0)\)

    证明：\(a \cdot c - b \cdot c = 0 \Leftrightarrow (a - b) \cdot c = 0\)，因为 \(c \ne 0\) 且不为零因子，所以 \(a = b\)。

    注：整环的消去律依赖于分配律成立，故一般的交换幺半群不满足消去律。

  • 乘法群（单位群）：\(R\) 中所有可逆元的集合与 \(\cdot\) 所构成的群。

插头 DP

Test 2025.5.13

  • P5468 [NOI2019] 回家路线

    细节很多的一道斜率优化 DP，调了半天，拍还很难拍出错。（出题人数据造太弱放过了暴力，也是逆天了。。。）

    朴素 DP 是 trival 的：以时间为阶段，计算某时刻在某位置所用的最小代价。然后这个式子显然可以使用斜率优化。

    一些问题：

    1. （对于下凸包）计算斜率分母为 0 时，需要取纵坐标较小者。

    2. 仔细判断横坐标、直线斜率的单调性。

    3. 先写暴力再写正解啊。。。我今天怎么就没有这么做呢。。。

    （看上去也不是很多？。。。那只能说我脑抽调了一上午了。）

  • P9479 [NOI2023] 桂花树

    这道题最困难的部分在于第一个转化……一般的 DP 思路是

分散层叠

给定 \(k\) 个有序数组，每个长度为 \(n\)。有 \(q\) 次询问，每次给定一个数 \(x\)，求 \(x\) 在每个数组中的后继。

两种暴力：

  • 直接 \(k\) 次二分：时间 \(O(kq \log n)\)，空间 \(O(kn)\)。

  • 先归并为一个数组，预处理每个数后面第一个第 \(i (1 \le i \le k)\) 组的数，再进行二分：时间 \(O(kn \log kn + q \log kn)\)，空间 \(O(k^2n)\)。

分散层叠算法则能够做到时间 \(O(kn \log kn + q \log kn)\)，空间 \(O(kn)\)。

具体而言，我们预处理 \(k\) 个数组 \(b_i\)，使得 \(b_i\) 为 \(b_{i+1}\) 中的所有偶数项 和 \(a_i\) 归并后的结果。由于 \(|b_i| = |a_i| + \frac{1}{2}|b_{i+1}|\)，所以显然 \(|b_i|_{\max} = |b_1| \le 2n\)，容易接受。

接着由于每个数组 \(b_i\) 只是两个数组的归并结果，我们容易对 \(b_i\) 中的每个元素维护下一个在 \(b_{i+1} / a_i\) 中的元素，空间复杂度 \(O(kn)\)。

最后询问的时候简单跳 \(k\) 次即可。

哈希

以下大部分内容来自 DeepSeek。

好的，在算法竞赛（OI）中，哈希技术常被用来高效地判断复杂结构（如集合、序列、树、图）的“相等性”，尤其是在无法直接比较或需要快速判断时。以下是几种常用且重要的哈希类型总结：

🧩 核心目的

  • 快速近似相等性判断： 在概率意义下（存在极低的哈希冲突概率），如果两个结构的哈希值不同，则它们必然不同；如果哈希值相同，则它们极大概率相同。
  • 降低复杂度： 将复杂结构的比较转化为整数或固定长度元组的比较。
  • 辅助数据结构： 作为键（Key）用于哈希表（unordered_map, unordered_set）或用于离散化。

🧮 1. 多重集哈希 (Multiset Hash / Bag Hash)

  • 目标： 判断两个不考虑元素顺序，但考虑元素出现次数的集合（多重集）是否相同。
  • 核心思想： 为每个元素值和每个出现位置（或次数） 分配一个随机贡献，组合起来代表整个多重集。
  • 常用方法:

    • 基于随机基数 + 组合函数：

      1. 为每个可能的元素值 \(e\) 分配一个或多个随机基数（Base） \(B_e\)（通常是一个较大的随机整数或通过 rand() 生成）【笔者注：如果使用 rand() 我们就还需要处理出一个 map，比较慢且比较麻烦，所以还有一些别的生成随机数方式，比如我们计算一个随机多项式 \(Trans(x) = A \times x \times x + B \times x + C\)，或者使用 xor_shift 即 x ^= x<<12, x ^= x>>5, x ^= x<<8】。
      2. 为元素出现的第 \(k\) 次（或简单地看作第 \(k\) 个位置）分配一个随机权重 \(W_k\)（或使用一个与 \(k\) 相关的确定性函数）。【笔者注：实际如果不使用异或哈希，一般可以忽略】
      3. 对于多重集中的每个元素实例（值为 \(e\)，是它在该集合中的第 \(k\) 次出现），计算其贡献 \(H_{e, k}\)。
      4. 使用一个可交换且结合的运算 \(\oplus\)（如加法 \(+\), 异或 \(\oplus\), 乘法 \(\times\)）将所有元素的贡献组合起来：\(H(\text{set}) = H_{e1, k1} \oplus H_{e2, k2} \oplus ... \oplus H_{en, kn}\)。
      • 加法： \(H(\text{set}) = \sum (B_e \times W_k)\)。简单，冲突概率相对较低。常用 \(W_k = 1\)（忽略出现顺序，只计数）或 \(W_k = k\)。
      • 异或 (XOR)： \(H(\text{set}) = \bigoplus (B_e \times W_k)\)。计算极快，但冲突概率相对加法更高（著名的 Anti-Hash 测试常针对 XOR）。也可用 \(W_k = 1\) 或 \(k\)。
      • 乘法： \(H(\text{set}) = \prod (B_e \times W_k)\)。冲突概率最低之一，但容易数值溢出，计算较慢。
      • 双哈希： 显著降低冲突概率，强烈推荐！

    • 基于质数乘法 (较少用但理论有趣)： 为每个元素值分配一个唯一的大质数 \(P_e\)。则 \(H(\text{set}) = \prod (P_e^{\text{count}(e)})\)。

  • 关键特性：
    • 可加性/可减性： 如果组合函数使用加法或异或，则哈希值支持 \(O(1)\) 的添加或删除元素操作。例如，从集合 \(S\) 的哈希值 \(H(S)\) 中添加元素 \(e\)（第 \(k\) 次出现）：\(H(S \cup \{e\}) = H(S) + B_e \times W_k\)。
    • 顺序无关： 组合运算 \(\oplus\) 的可交换性保证了元素顺序不影响最终哈希值。
    • 计数敏感： 元素出现次数通过 \(k\) 或重复使用 \(B_e\) 体现在哈希中。
  • 应用场景： 判断两个集合是否相同（无序带计数）；滑动窗口中的元素频率统计（结合可加/减性）；动态集合维护。

📜 2. 有序序列哈希 (Ordered Sequence Hash / String Hash)

  • 目标： 判断两个考虑元素顺序的序列（通常是字符串或数组）是否完全相同，或者快速计算其任意子串/子区间的哈希值。
  • 核心思想： 多项式滚动哈希（Rabin-Karp 算法的核心）。
  • 常用方法:
    1. 选择两个（或多个）大质数作为模数 MOD（如 1e9+7, 998244353, 1e9+9）。双模数更安全。
    2. 选择一个基数（Base） \(B\) (\(B >\) 字符集大小，通常取质数如 131, 13331, 233)。双基数更安全。
    3. 对于序列 \(S[0..n-1]\)：
    • 计算前缀哈希数组 Pre：
      • Pre[0] = 0 (或 \(S[0]\) 的映射值，但通常从 \(0\) 开始更统一)
      • \(Pre[i] = (Pre[i-1] \times B + S[i]) \bmod \text{MOD}\) (常用)
      • 或 \(Pre[i] = (Pre[i-1] + S[i] \times B^i) \bmod \text{MOD}\) (另一种形式，较少用)
    • 计算后缀哈希数组（如果需要反向匹配）。
    1. 计算子串/子区间 \(S[l..r]\) 的哈希值 \(H(l, r)\)：
    • 常用形式 (\(Pre[0]=0\)): \(H(l, r) = (Pre[r] - Pre[l-1] \times B^{(r-l+1)}) \bmod \text{MOD} + \text{MOD}) \bmod \text{MOD}\)
    • 需要预处理 \(B\) 的幂次 \(Pow[i] = B^i \bmod \text{MOD}\)。
  • 关键特性：
    • 顺序敏感： 序列元素的顺序直接影响哈希值。
    • 高效子串查询： 通过 \(O(1)\) 时间（预处理 \(O(n)\)）计算任意子串的哈希值。
    • 可连接性： 如果已知 \(H(S_1)\) 和 \(H(S_2)\)，且 \(S_1\) 长度为 \(L_1\)，则 \(H(S_1 + S_2) = (H(S_1) \times B^{L_2} + H(S_2)) \bmod \text{MOD}\)。
  • 注意事项：
    • 冲突概率： 单哈希在长串或特殊构造数据下冲突概率较高。强烈推荐使用双哈希（两个不同的 \(B\) 和 MOD），存储一个哈希对 \((H_1, H_2)\)。
    • 自然溢出： 利用无符号整型的自动取模（模 \(2^{32}\) 或 \(2^{64}\)）。计算速度快，但易被精心构造的数据卡（Anti-Hash），比赛慎用。
  • 应用场景： 字符串匹配（Rabin-Karp）；判断字符串/数组是否相等；判断子串是否相等（结合前缀和）；回文判断（正反哈希比较）；字符串编辑距离的近似计算（结合其他技巧）。

🌲 3. 树哈希 (Tree Hash / Isomorphism Hash)

  • 目标： 判断两棵树（通常是无根树或有根树） 在某种同构意义下（如子树同构、有根树同构、无根树同构）是否结构相同。
  • 核心思想： 递归地计算每个子树（以某个节点为根）的哈希值，将子树的结构信息“压缩”成一个哈希值。核心在于如何将子节点的哈希值组合成父节点的哈希值，且保证同构的树哈希值相同。
  • 常用方法 (递归定义，以计算有根树 \(u\) 的哈希 \(H(u)\) 为例):
    1. 叶子节点： 通常赋予一个常量（如 \(1\), \(\text{BASE}\)）。
    2. 非叶子节点：
    • 收集子树的哈希： 计算 \(u\) 的所有直接子节点 \(v_1, v_2, ..., v_k\) 的子树哈希 \(H(v_1), H(v_2), ..., H(v_k)\)。
    • 处理顺序：
      • 排序法 (确保同构子树顺序无关)： 将 \(H(v_1) ... H(v_k)\) 按哈希值从小到大排序得到一个序列 \(H_{\text{sorted}}\)。然后组合：\(H(u) = (\text{常数} + F(H_{\text{sorted}})) \times G(...) \bmod \text{MOD}\)。
      • 非排序法 (更高效，但仅适用于有根树且孩子顺序固定或无关)： 同上文的多重集哈希。这里就建议使用 xor_shift 或多项式生成随机数。
      • 【笔者注：还有一种方法是维护树的括号序列。】
  • 无根树同构处理：
    • 方法 1： 取以每个节点为根计算得到的有根树哈希值中的最小值（或最大值） 作为整棵无根树的哈希值。
    • 方法 2 (更高效)： 找到树的重心（Center(s)）。无根树最多有两个重心。
      • 如果有一个重心 \(c\)，则 \(H_{\text{tree}} = \text{TreeHash}(c)\)。
      • 如果有两个重心 \(c_1, c_2\)，则 \(H_{\text{tree}} = F(\text{TreeHash}(c_1, c_2), \text{TreeHash}(c_2, c_1))\)（例如取和、积、有序对等）。注意在以 \(c_1\) 为根时，\(c_2\) 是其孩子；反之亦然。计算 \(\text{TreeHash}(c_1)\) 时 \(c_2\) 是它的一个子节点，计算 \(\text{TreeHash}(c_2)\) 时 \(c_1\) 是它的一个子节点。
  • 关键特性：
    • 结构敏感性： 哈希值编码了树（或子树）的拓扑结构。
    • 递归性： 子树哈希的计算依赖于其子树的哈希。
    • 顺序无关 (如果使用排序法)： 对子树哈希排序保证了同构树即使孩子顺序不同也能得到相同哈希值。
  • 注意事项：
    • 冲突： 树哈希冲突理论存在，且可能有针对性构造。使用双哈希（不同 \(\text{SEED}\), \(\text{BASE}\), \(\text{MOD}\)）或加入子树大小、深度等信息扰动可以显著降低冲突概率。
    • 复杂度： 单次 DFS \(O(n)\)。排序法在节点度数大时排序有 \(O(\deg \times \log(\deg))\) 开销，总复杂度 \(O(n \log n)\)。非排序法 \(O(n)\)。
  • 应用场景： 判断树同构（有根/无根）；树的最小表示/规范形；查找重复子树；树分治中的结构标识。

📌 总结与通用建议

  1. 随机性是关键： 所有方法的基数（\(B\), \(B_e\)）、种子（\(\text{SEED}\)）、权重（\(W_k\), \(W_i\)）、模数（\(\text{MOD}\)） 都应使用高质量的随机数（如 std::mt19937）生成，以抵抗针对性构造（Anti-Hash）的数据。固定值容易被卡。
  2. 双哈希/多哈希： 这是提高安全性、降低冲突概率的最有效且实用的方法！ 对于任何重要的应用，尤其是比赛环境，强烈建议使用两个（甚至三个）完全独立的哈希函数（不同的基数和模数），并将结果组成一个 pair 或 tuple 作为最终的哈希值。
  3. 模数选择： 使用大质数（至少大于可能的最大哈希值范围，如 1e9+7）。双模数时，两个模数应互质且都足够大。
  4. 理解冲突概率： 哈希本质是概率算法，冲突永远存在。设计哈希函数时要权衡冲突概率、计算效率和实现复杂度。双哈希将冲突概率从 \(1/\text{MOD}\) 降低到 \(1/(\text{MOD}_1 \times \text{MOD}_2)\)。
  5. 结合问题特性： 选择哪种哈希以及具体参数（组合函数、是否排序、是否包含额外信息如深度大小）需要根据具体问题（是否需要顺序、是否考虑计数、结构类型）来调整。
  6. 慎用自然溢出： 虽然快，但在 OI 等高强度对抗环境中极易被特殊数据卡掉，除非能证明其安全性或题目数据弱，否则建议使用显式模大质数。

掌握这些哈希技术能让你在 OI 中高效解决许多涉及复杂结构比较的问题，特别是在字符串、树和图论领域。务必多练习实现，并理解其背后的原理和局限性！💪🏻

posted @ 2025-05-07 20:23  David_Mercury  阅读(76)  评论(0)    收藏  举报