莫队学习笔记
前言
之前暑假集训的时候学习的算法,由于学的时候就有点马马虎虎之后也根本没用到过就基本忘干净了,没想到今天比赛居然用到了……补上这一篇。
解说
什么时候能用?
先明确这一问题。
似乎一般用在有一大堆询问的时候且每次询问涉及两个变量,且可以通过其中一次询问的结果推导到另一个询问(概括能力有限,大约是这样吧……)。
怎么用?
双指针
第一部分和双指针相关,以洛谷 \(P1972\) 为例,大致题意就是给一个序列和一堆询问,每次询问这个序列上 \([l,r]\) 间有多少不同数字。
暴力的话肯定是开一个 \(cnt\) 数组,每次询问清空一下 \(cnt\) ,之后从 \(l\) 扫到 \(r\) ,遇见 \(cnt\) 为 \(0\) 的数字答案就加一,之后将其 \(cnt\) 加一。
现在考虑用双指针。假设我们的 \(L\) 指针最开始在 \(1\) 位置, \(R\) 指针最开始在 \(0\) 位置, \(ans\) 为 \(0\) ,那么我们就可以用指针去匹配每一个询问区间,在移动指针的过程中顺便更新答案。
假设有两个询问区间 \([1,9],[6,15]\) 。
(由于本人太菜了不会画图且没什么画图时间所以接下来的图片和部分文字转载自这篇博客)
假设这个序列是这样子的:(其中 \(Q1\) 、\(Q2\) 是询问区间)

我们发现 \(L\) 已经是第一个查询区间的左端点,无需移动。现在我们将 \(R\) 右移一位,发现新数值 \(1\):

\(R\) 继续右移,发现新数值 \(2\):

\(R\) 继续右移,发现新数值 \(4\):

当 \(R\) 再次右移时,发现此时的新位置中的数值 \(2\) 出现过,数值总数不增:

以此类推,知道我们的 \(R\) 移动到了 \(Q1\) 的右端点上,至此我们就得到了第一个询问的答案。

现在我们看一下 \(Q2\) 区间的情况:
首先我们发现, \(L\) 指针在 \(Q2\) 区间左端点的左边,我们需要将它右移,同时删除原位置的统计信息。
将 \(L\) 右移一位到位置 \(2\) ,删除位置 \(1\) 处的数值 \(1\) 。但由于操作后的区间中仍然有数值 \(1\) 存在,所以总数不减。

依然是以此类推移动左指针直到其和 \(Q2\) 的左端点重合同时维护信息,之后以此类推移动右端点即可。这样我们就可以用双指针维护出答案了。
分块
看完之后是不是觉得上面的双指针没有卵用?因为询问的区间乱序给出的话我们的两个指针就会在整个序列上 反 复 横 跳 ,根本没有任何优化效果。那么只有一个解决办法: 将询问离线! ,这样我们就可以将所有询问排序减小指针移动范围。但是问题在于如何排序?按左端点排?那么我们的右指针仍然会在整个序列上 反 复 横 跳 ,没有任何优化效果。这时候就需要用到我们的分块了。感性地理解 由于中国人的性情是喜欢折中的 所以这是一种折中的办法,它使得左指针跳动的范围不至于太大,右端点跳动的范围也不至于太大。
我们将整个序列分成 \(s\) 个块,之后将询问按照如下格式进行排序:
bool operator < (const node &A) const{
if(belong[l]!=belong[A.l]) return belong[l]<belong[A.l];
return r<A.r;
}
之后就可以愉快的用双指针处理了
跟分块问题一样块的大小同样会影响莫队的时间复杂度, 简单 计算一下就能发现在这个问题 \(s\) 大小取 \(\sqrt{n}\) 可以达到最优时间复杂度 \(\Theta(n\sqrt{n})\) 。其他时候块的最优大小还是具体问题具体分析吧(本 \(juruo\) 也不大会所以咕咕咕了)。
注意
- 一般指针移动的时候应该遵循先扩后缩原则
- 注意 \(L\) 和 \(R\) 的初始状态带来的影响
例题

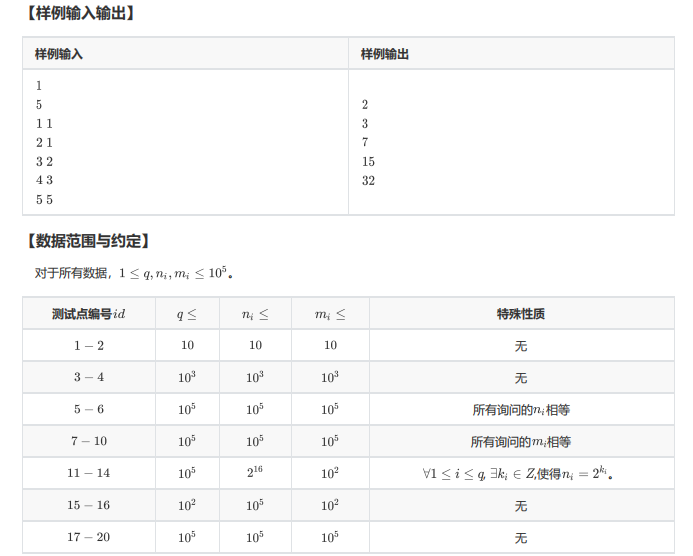
解说
一眼看上去这谁能看出来是莫队啊
结合部分分的提示简单推一下式子就会发现:
如果我们把 \(L\) 看作 \(m\) 把 \(R\) 看作 \(n\) 就会发现它非常符合莫队的特征,完美解决!但是写代码的时候要尤其注意上面提到的要注意的两点,因为 \(n\) 必须大于等于 \(m\)所以不小心的话容易挂……
代码
#include<bits/stdc++.h>
#define re register
#define ll long long
using namespace std;
const int lzw=1e5+3,mod=1e9+7;
int t,fac[lzw],ine[lzw],ans,belong[lzw],Max,res[lzw],inv,id;
inline int power(int a,int p){
int ans=1;
while(p){
if(p&1) ans=1LL*ans*a%mod;
p>>=1;
a=1LL*a*a%mod;
}
return ans;
}
inline int comb(int n,int m){
return 1LL*fac[n]*ine[m]%mod*ine[n-m]%mod;
}
struct node{
int l,r,id;
bool operator < (const node &A) const{//这里用了一个叫奇偶性优化的东西,大约就是说从一个块跳下一个块的右端点时可以快一些
return (belong[l] ^ belong[A.l]) ? belong[l] < belong[A.l] : ((belong[l] & 1) ? r < A.r : r > A.r);
}
}all[lzw];
inline void init(){
int s=sqrt(Max);
for(re int i=1;i<=Max;i++) belong[i]=(i-1)/s+1;
sort(all+1,all+1+t);
}
inline int read(){
int f=1,x=0;char c=getchar();
while(!isdigit(c)) f=(c=='-'?-1:1),c=getchar();
while(isdigit(c)) x=x*10+c-'0',c=getchar();
return f*x;
}
int main(){
freopen("sum.in","r",stdin);
freopen("sum.out","w",stdout);
id=read(),t=read();
for(re int i=1;i<=t;i++) all[i].r=read(),all[i].l=read(),all[i].id=i,Max=max(Max,all[i].r);
init();
fac[0]=1;
for(re int i=1;i<=lzw-3;i++) fac[i]=1LL*fac[i-1]*i%mod;
ine[lzw-3]=power(fac[lzw-3],mod-2);
for(re int i=lzw-3;i;i--) ine[i-1]=1LL*ine[i]*i%mod;
inv=power(2,mod-2);
int l=0,r=1,ans=1;
for(re int i=1;i<=t;i++){
int ql=all[i].l,qr=all[i].r;
while(r<qr) ans=(2LL*ans-comb(r,l)+mod)%mod,r++;
while(l>ql) ans=((ll)ans-comb(r,l)+mod)%mod,l--;
while(r>qr) ans=((ll)ans+comb(r-1,l))%mod*inv%mod,r--;
while(l<ql) ans=((ll)ans+comb(r,l+1))%mod,l++;
res[all[i].id]=ans;
}
for(re int i=1;i<=t;i++) printf("%d\n",res[i]);
return 0;
}
另
关于之间复杂度问题,郭巨佬认为块的大小为\(\sqrt{q}\)时最佳,我则认为大小为根号\(n\)的最大值时最佳,结果好像交上去后后者更好……
幸甚至哉,歌以咏志。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号