关于DP题的状态定义转换和各种优化这档事
前言
由于\(DarthVictor \ DP\)太菜,最近在刷各种\(DP\)题提升水平,于是见到了各种奇妙的状态定义转换和各种奇妙的\(DP\)优化,遂处处志之。
\(\large \color{red}{\texttt{可能随遇到新的DP题随时更新}}\)
状态定义转化
前言
由于\(DP\)时某一维数据太大,按照正常思路可能会出现数组开不下的情况,这时候可以试着改变一下状态定义,以求出路。主要方法有交换两维,寻找新维等(起名无力……)。
交换两维
跑背包时经常用到,可能会背包容量/物品体积过大而价值较小,这时候可以把体积和价值交换一下,\(f[i]\)定义为达到价值\(i\)至少需要多少体积,最后用背包容量二分或用其他方法查询即可即可。
例题:经典版

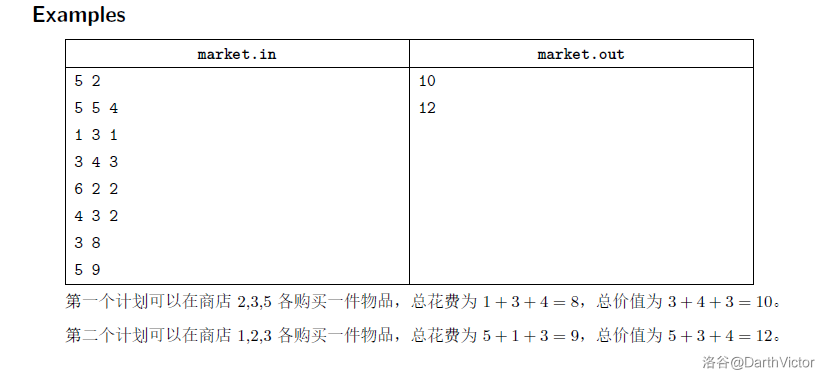
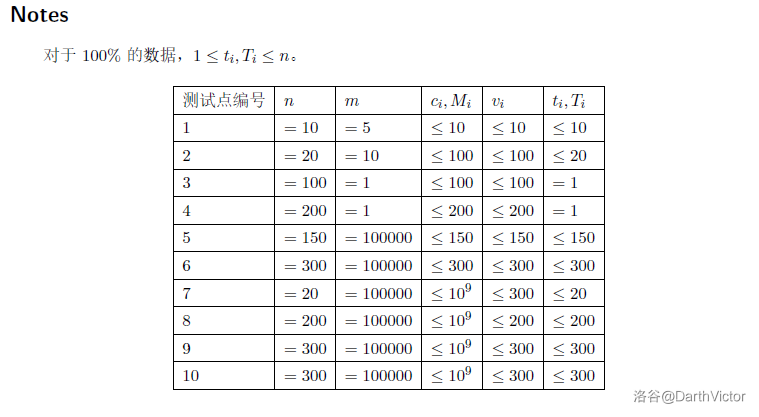
解说
非常典型的一道例题,物品体积(本题中为要花的钱)和背包容量(预算)非常之大而价值非常小,符合上面的特点,所以交换正常情况下价值和体积这两维最后二分即可。
注意! 刚跑出来的\(f[i]\)数组是不单调的,在进行二分之前要先进行一定的处理:
for(re int k=sum;k;k--) f[k]=min(f[k],f[k+1]);
举例来说,我们现在买价值为\(k\)的东西需要一百万,而买价值为\(k+1\)的东西要花一块钱,那么显然\(f[k]=1,000,000\)就莫得用处了,直接抹掉就好。
顺带一提,本题中还涉及了时间这码事,由于本题中时间是单调的,排个序依次搞即可。
完整代码
#include<bits/stdc++.h>
#define re register
using namespace std;
const int maxn=300+3,maxm=1e5+3;
int n,m,ans[maxm],f[maxn*maxn],sum;//f[i]为价值是i时的最小空间
struct mall{
int c,v,t;
bool operator < (const mall &A) const{
return t<A.t;
}
}a[maxn];
struct buy{
int t,m,id;
bool operator < (const buy &A) const{
return t<A.t;
}
}b[maxm];
int main(){
freopen("market.in","r",stdin);
freopen("market.out","w",stdout);
scanf("%d%d",&n,&m);
for(re int i=1;i<=n;i++) scanf("%d%d%d",&a[i].c,&a[i].v,&a[i].t),sum+=a[i].v;
for(re int i=1;i<=m;i++) scanf("%d%d",&b[i].t,&b[i].m),b[i].id=i;
sort(a+1,a+1+n);
sort(b+1,b+1+m);
memset(f,0x3f,sizeof(f));
f[0]=0;
int j=1;
for(re int i=1;i<=m;i++){
while(j<=n&&a[j].t<=b[i].t){
for(re int k=sum;k>=a[j].v;k--) f[k]=min(f[k],f[k-a[j].v]+a[j].c);
for(re int k=sum;k;k--) f[k]=min(f[k],f[k+1]);//保持单调性
j++;
}
ans[b[i].id]=upper_bound(f+1,f+1+sum,b[i].m)-f-1;
}
for(re int i=1;i<=m;i++) printf("%d\n",ans[i]);
return 0;
}
例题:树上版



解说
特点还是体积大,只不过这次被扔到树上了(不会有人看不出来这是个树上的题吧?不会吧不会吧……)
因为本题问最多可以买几个商品,因此本题中隐含的价值就是每个商品价值均为\(1\),非常小,符合上面的特点,故定义\(f[i][j][1/0]\)为\(i\)的子树中购买\(j\)件商品用/不用优惠券至少需要多少钱,跑树型\(DP\)即可。最后由于这个\(f[i]\)数组是三维的不太好二分就直接全部和总钱数比一下大小。
完整代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int lzw=5e3+3;
int head[lzw],c[lzw],d[lzw],n,b,tot,f[lzw][lzw][2],size[lzw];
struct edge{
int to,next;
}e[lzw];
void add(int a,int b){
e[++tot].to=b;
e[tot].next=head[a];
head[a]=tot;
}
void dfs(int u){
size[u]=1;
f[u][0][0]=0;
f[u][1][0]=c[u],f[u][1][1]=c[u]-d[u];
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
dfs(v);
for(int j=size[u];j>=0;j--){
for(int k=0;k<=size[v];k++){
f[u][j+k][0]=min(f[u][j+k][0],f[u][j][0]+f[v][k][0]);
f[u][j+k][1]=min(f[u][j+k][1],f[u][j][1]+min(f[v][k][0],f[v][k][1]));
}
}
size[u]+=size[v];
}
}
signed main(){
scanf("%lld%lld",&n,&b);
for(int i=1;i<=n;i++){
scanf("%lld%lld",&c[i],&d[i]);
if(i>1){
int tmp;
scanf("%lld",&tmp);
add(tmp,i);
}
}
memset(f,0x3f,sizeof(f));
dfs(1);
int ans;
for(int i=n;i>=0;i--){
if(f[1][i][0]<=b||f[1][i][1]<=b){
printf("%lld\n",i);
return 0;
}
}
}
寻找新维
自己瞎起的名字……
主要出现在各种题目的加强版里,一个变量扩大到数组开不下之后就试试能不能找到一个新的加到状态定义里面替换原来的。
(感觉和交换二维差不多啊……)
例题
是下面这个的加强版:
解说
原来的题就是一个简简单单的经典区间\(DP\),而数据扩大之后不仅数组开不下而且也跑不动啊……
于是我们观察一下这道题里面有什么量的数据范围比较小可以用来利用一下……\(emm\),显然数字的范围非常小,我们应该试着用它来定义状态。
于是就有了这个奇妙的东西:
定义\(f[i][j]\)代表以\(i\)为左端点能组合出数字\(j\)的最小右端点
那么有
这正常人谁能想到啊[托腮][托腮] 以后还是好好锻炼思维能力吧……
顺带一提\(j\)可不止只到\(40\)啊,本题中最大的数据范围\(262144=2^{18}\),也就是说最大的合并出的数据只会达到\(58\),完全可以接受。
完整代码
#include<bits/stdc++.h>
#define re register
using namespace std;
const int lzw=248+3;
int n,f[50+3][lzw],ans;
char buf[1<<20], *p1, *p2;
char gc() { return p1 == p2 ? p2 = buf + fread(p1 = buf, 1, 1<<20, stdin), (p1 == p2) ? EOF : *p1++ : *p1++; }
inline int read(int f = 1, char c = gc(), int x = 0) {
while(c < '0' || c > '9') f = (c == '-') ? -1 : 1, c = gc();
while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = gc();
return f * x;
}
int main(){
n=read();
for(re int i=1;i<=n;i++){
int tmp=read();
f[tmp][i]=i+1;
}
for(re int i=2;i<=50;i++){
for(re int j=1;j<=n;j++){
if(f[i][j]||f[i-1][f[i-1][j]]) ans=i;
if(!f[i][j]) f[i][j]=f[i-1][f[i-1][j]];
}
}
printf("%d\n",ans);
return 0;
}
各种奇妙优化
堆优化
总结一下特点似乎是决策的时候涉及在两个量之间进行选择,于是我们就开两个堆分别维护两种变量,并且人为规定一个主变量一个次变量,每次决策时从两个堆顶选最佳的同时维护堆合法。如果主变量目前不够优就把它扔进次变量的堆里。
例题
为了说服珍娜女王停止改造计划,\(Eddie\)和\(Hobo\)踏上了去往王宫的征程。\(Sunshine Empire\)依次排列着\(N+1(N \le 5 \times10^5)\)座城市,\(0\) 号城市是出发地,\(N\) 号城市是王宫。
火车是 \(Sunshine Empire\) 的主要交通工具。\(Eddie\) 和 \(Hobo\) 可以在当前的城市上车,并且在之后的某一座城市下车。从第\(i-1\)座城市乘坐到第\(i\)座城市需要花费\(A_i\)的费用。同时,在第\(i\) 座城市上车需要缴纳\(B_i\)的税款。其中,税款属于额外支出,不属于乘坐这段火车的费用\((A_i,B_i<=10^6)\)。
随遇到新的DP题随时更新
珍娜女王为了促进\(Sunshine Empire\)的繁荣发展,下令:如果连续地乘坐一段火车的费用大于这次上车前所需缴纳的税款,则这次上车前的税款可以被免除,否则免去乘坐这段火车的费用。
然而,为了保证火车的正常运行,每一次乘坐都不能连续经过超过\(K(K \le 10^5)\)座城市(不包括上车时所在的城市),并且,\(Eddie\)和\(Hobo\) 的移动范围都不能超出\(Sunshine Empire\)。\(Eddie\)想知道,到达王宫的最小总花费是多少?
解说
首先\(n^2\)线性\(DP\)非常好想:
我们发现转移的时候无非从\(f[j]+b[j]\)或\(f[j]+sum[j]\)这两种状态转移过来,符合上面所说的在两个量之间选择进行决策,那么我们就开两个大根堆,一个扔\(f[j]+b[j]\),一个扔\(f[j]+sum[j]\)。规定\(f[j]+b[j]\)为主变量。若\(q1.top()>=f[j]-sum[j]+sum[i]\)那就直接用它;若\(q1.top()<f[j]-sum[j]+sum[i]\) 那就把他的被动决策塞入另一个堆中维护,因为不确定以后它的次变量会不会被用到。
同时注意一下\(K\)的问题,这关系到堆的合法性,其实还是很好维护的,每次决策前后都把不合法的——和目前\(i\)的距离大于\(K\)的——清理掉就行了。那么这样两个堆中的状态都是合法的,然后直接取堆顶元素就是最优的。
随手引用一段学长的话:
而可能你会想到那第一个堆中的元素\(pop\)掉了,会不会有后效性,其实不会,因为\(sum[i]-sum[j]\)的\(sum[j]\)固定而\(sum[i]\)递增,所以当他从\(q1 \ pop\)出去后,他在\(q2\)中就会一直呆着了。
完整代码
#include<bits/stdc++.h>
#define re register
#define ll long long
using namespace std;
inline int read(){
int f=1,x=0;char c=getchar();
while(c<'0'||c>'9') f=(c=='-'?-1:1),c=getchar();
while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar();
return f*x;
}
struct node{
int id;
ll val;
node(){}
node(int x,ll y){id=x,val=y;}
bool operator < (const node &A)const{
return val>A.val;
}
};
priority_queue<node> q1,q2;
const int lzw=5e5+3;
int n,k,b[lzw],tmp;
ll sum[lzw],f[lzw];
int main(){
freopen("empire.in","r",stdin);
freopen("empire.out","w",stdout);
n=read(),k=read();
for(re int i=1;i<=n;i++) tmp=read(),sum[i]=sum[i-1]+tmp;
for(re int i=1;i<=n;i++) b[i]=read();
memset(f,0x3f,sizeof(f));
f[0]=0;
for(re int i=1;i<=n;i++){
q1.push(node(i-1,f[i-1]+b[i]));
while(q1.size()){
if(q1.top().id>=i-k) break;
q1.pop();
}
while(q2.size()){
if(q2.top().id>=i-k) break;
q2.pop();
}
while(q1.size()){
node now=q1.top();
if(now.val>f[now.id]+sum[i]-sum[now.id]) break;
q1.pop();
q2.push(node(now.id,f[now.id]-sum[now.id]));
}
while(q1.size()){
if(q1.top().id>=i-k) break;
q1.pop();
}
while(q2.size()){
if(q2.top().id>=i-k) break;
q2.pop();
}
if(!q1.empty()) f[i]=min(f[i],q1.top().val);
if(!q2.empty()) f[i]=min(f[i],sum[i]+q2.top().val);
}
printf("%lld\n",f[n]);
return 0;
}
单调栈优化
留坑,解说先咕掉,扔下例题和代码跑路。
例题



代码
#include<bits/stdc++.h>
#define int long long
#define re register
#define top stk[0]
using namespace std;
const int lzw=1e6+3;
int n,c,a[lzw],f[lzw],sum[lzw],qsum[lzw],stk[lzw],ans;
int cal(int i,int j,int k){
int len=i-j-1,up=2*(sum[i-1]-sum[j])+c,down=qsum[i-1]-qsum[j]+a[i]*c;
if(j) up+=c,down+=a[j]*c;
int t=max((int)(1.0*up/2/len+0.5),a[k]);
t=min(t,min(a[i],a[j]));
return len*t*t-up*t+down;
}
signed main(){
freopen("construct.in","r",stdin);
freopen("construct.out","w",stdout);
scanf("%lld%lld",&n,&c);
for(re int i=1;i<=n;i++) scanf("%lld",&a[i]),sum[i]=sum[i-1]+a[i],qsum[i]=qsum[i-1]+a[i]*a[i];
a[0]=LLONG_MAX/2,a[n+1]=LLONG_MAX/2-1;
top=1;
while(top&&a[stk[top]]<=a[1]){
f[1]=min(f[1],f[stk[top-1]]+cal(1,stk[top-1],stk[top]));
top--;
}
stk[++top]=1;
for(re int i=2;i<=n;i++){
f[i]=f[i-1]+c*abs(a[i]-a[i-1]);
while(top&&a[stk[top]]<=a[i]){
f[i]=min(f[i],f[stk[top-1]]+cal(i,stk[top-1],stk[top]));
top--;
}
stk[++top]=i;
}
ans=f[n];
while(top&&a[stk[top]]<=a[n+1]){
int len=n-stk[top-1],up=2*(sum[n]-sum[stk[top-1]]),down=qsum[n]-qsum[stk[top-1]];
if(stk[top-1]) up+=c,down+=a[stk[top-1]]*c;
int t=max((int)(up/2/len+0.5),a[stk[top]]);
t=min(t,min(a[stk[top-1]],a[n+1]));
t=len*t*t-up*t+down;
ans=min(ans,f[stk[top-1]]+t);
top--;
}
printf("%lld\n",ans);
return 0;
}
斜率优化
挺常遇到的一种\(DP\),也比较套路,一般只要能看出来是斜率优化直接套板子即可。特点是通常将转移方程拆开之后都可以表示成\(y=ax+b\)的形式,只要搞清楚哪个变量作为\(y\)哪个作为\(x\)就可以直接套板子。
例题
代码
以仓库建设为例
#include<bits/stdc++.h>
#define re register
#define ll long long
using namespace std;
const int lzw=1e6+3;
int n,c[lzw],x[lzw],p[lzw],qq[lzw],l,r;
ll s[lzw],q[lzw],f[lzw];
ll y(int x){
return f[x]+q[x];
}
ll cal(int i,int j){
return y(j)+c[i]+x[i]*(s[i]-s[j])-q[i];
}
#define gc() (p1==p2?(p2=buf+fread(p1=buf,1,1<<20,stdin),p1==p2?EOF:*p1++):*p1++)
#define read() ({re int x=0,f=1;re char c=gc();while(!isdigit(c)){f=(c=='-'?-1:1),c=gc();}while(isdigit(c)) x=x*10+(c&15),c=gc();f*x;})
char buf[1<<20],*p1,*p2;
signed main(){
n=read();
for(re int i=1;i<=n;i++) x[i]=read(),p[i]=read(),c[i]=read();
for(re int i=1;i<=n;i++) s[i]=s[i-1]+p[i],q[i]=q[i-1]+p[i]*x[i];
l=r=1;
for(re int i=1;i<=n;i++){
while(l<r&&y(qq[l])-y(qq[l+1])>=1LL*x[i]*(s[qq[l]]-s[qq[l+1]])) l++;
f[i]=cal(i,qq[l]);
while(l<r&&(y(qq[r])-y(qq[r-1]))*(s[i]-s[qq[r]])>=(y(i)-y(qq[r]))*(s[qq[r]]-s[qq[r-1]])) r--;
qq[++r]=i;
}
printf("%lld\n",f[n]);
return 0;
}
矩阵快速幂优化
一般用于递推数列类转移系数固定的\(DP\)方程进行加速,一般看见\(n\)达到\(10^{18}\)级别的基本就是矩阵快速幂优化了。有的时候数据范围较小,可以用临接表存图的图论题也可以用矩阵快速幂优化。注意假设表上a[i][j]==1表示\(i \ j\)之间有连边那么将这个矩阵自乘\(p\)次之后则表示\(i -> j\)走\(p\)步的方案数。
递推式加速例题
解说
可以非常简单地写出递推/\(DP\)式子(\(cnt_i\)表示\(i\)十进制下的位数):
然而我们的数据范围中\(n\)达到了\(10^{18}\)的级别,时间上根本撑不住,于是考虑矩阵快速幂优化。
不难看出 这个方程可以被表示为下面的矩阵:
然而……这个转移系数不固定!\(cnt_i\)是在变化的!
没关系,分下块就好了。
代码
#include<bits/stdc++.h>
#define int long long
#define re register
using namespace std;
int n,mod,sum;
int cnt(int x){
int ans=0;
while(x) ans++,x/=10;
return ans;
}
struct M{
int d[5][5],n,m;
M(){memset(d,0,sizeof(d));}
};
M mul(M a,M b){
M ans;
ans.n=a.n,ans.m=b.m;
for(re int i=1;i<=a.n;i++)
for(re int j=1;j<=b.m;j++)
for(re int k=1;k<=a.m;k++)
ans.d[i][j]=(ans.d[i][j]+1LL*a.d[i][k]*b.d[k][j]%mod)%mod;
return ans;
}
M power(M a,int p){
M ans;
ans.n=a.n,ans.m=a.m;
for(re int i=1;i<=ans.n;i++) ans.d[i][i]=1;
while(p){
if(p&1) ans=mul(ans,a);
p>>=1;
a=mul(a,a);
}
return ans;
}
int num_power(int a,int p){
int ans=1;
while(p){
if(p&1) ans=ans*a;
p>>=1;
a=a*a;
}
return ans;
}
void print(M x){
cout<<x.n<<' '<<x.m<<endl;
for(re int i=1;i<=x.n;i++){
for(re int j=1;j<=x.m;j++) cout<<x.d[i][j]<<' ';
cout<<endl;
}
cout<<endl;
}
signed main(){
M st;
st.n=3,st.m=1,st.d[1][1]=0,st.d[2][1]=0,st.d[3][1]=1;
scanf("%lld%lld",&n,&mod);
sum=cnt(n);
M a;
a.n=a.m=3;
for(re int i=1;i<=sum-1;i++){
memset(a.d,0,sizeof(a.d));
a.d[1][2]=a.d[1][3]=a.d[2][2]=a.d[2][3]=a.d[3][3]=1;
a.d[1][1]=num_power(10,i)%mod;
a=power(a,9*num_power(10,i-1));
st=mul(a,st);
}
memset(a.d,0,sizeof(a.d));
a.d[1][2]=a.d[1][3]=a.d[2][2]=a.d[2][3]=a.d[3][3]=1;
a.d[1][1]=num_power(10,sum)%mod;
a=power(a,n-num_power(10,sum-1)+1);
st=mul(a,st);
printf("%lld\n",st.d[1][1]);
return 0;
}
图论加速例题
解说
本题如果没有爆炸这回事那么只要填出临接表,再直接用上文说的结论直接使用快速幂,最后统计\(1\)这一行的方案数之和即可。
现在考虑爆炸怎么处理
不难想到 由于机器人炸掉之后就不可能再到达其他的地方了,所以我们可以将它看作一个只能进入而没有出边的点。但是\(\large \color{Red}{\texttt{注意}}\)爆炸要向自己连一条边,否则在最后一步之前到达爆炸的方案数就无法被统计在内。
代码
#include<bits/stdc++.h>
#define re register
using namespace std;
const int mod=2017;
int n,m,t;
struct M{
int d[100+3][100+3],n,m;
M(){}
M(int x,int y){memset(d,0,sizeof(d)),n=x,m=y;}
};
M mul(M a,M b){
M ans=M(a.n,b.m);
for(re int i=1;i<=a.n;i++)
for(re int j=1;j<=b.m;j++)
for(re int k=1;k<=a.m;k++)
ans.d[i][j]=(1LL*ans.d[i][j]+1LL*a.d[i][k]*b.d[k][j]%mod)%mod;
return ans;
}
M power(M a,int p){
M ans=M(a.n,a.n);
for(re int i=1;i<=ans.n;i++) ans.d[i][i]=1;
while(p){
if(p&1) ans=mul(ans,a);
p>>=1,a=mul(a,a);
}
return ans;
}
void print(M x){
cout<<x.n<<' '<<x.m<<endl;
for(re int i=1;i<=x.n;i++){
for(re int j=1;j<=x.m;j++) cout<<x.d[i][j]<<' ';
cout<<endl;
}
cout<<endl;
}
int main(){
scanf("%d%d",&n,&m);
M a=M(n+1,n+1);
for(re int i=1;i<=n;i++) a.d[i][i]=1,a.d[i][n+1]=1;
a.d[n+1][n+1]=1;
for(re int i=1;i<=m;i++){
int x,y;
scanf("%d%d",&x,&y);
a.d[x][y]=a.d[y][x]=1;
}
scanf("%d",&t);
a=power(a,t);
int ans=0;
for(re int i=1;i<=n+1;i++) ans=(1LL*ans+a.d[1][i])%mod;
printf("%d\n",ans);
return 0;
}
幸甚至哉,歌以咏志。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号