3月补完计划
补完就会在清明节退役啦😃😃😃
[QOJ5173]染色
Solution
这也做不出来,这就是sbtr🙂🤗🤗🤗
注意到上界是 \(2\cdot (r-l)\),即每次把这个点变成要到的点的颜色。我们考虑到最多可以减少的答案,那么可以设 \(f_i\) 表示 \(l\to i\) 能减少的最多答案,可以得到转移式:
这个东西显然是存在单调性的,所以即相当于每次跳一步,用倍增优化即可。当然,这个是树形结构,也可以写成并查集。
复杂度 \(\mathcal O(n\alpha (n)/n\log n)\) 。
「2023年集训队互测 Round7」foo~
Solution
什么都做不出来😚😚😚
我们首先考虑破环成链,因为最大值所在的段一定有一边不会产生贡献,所以我们把不会产生贡献的那一段分到别的地方一定不劣,所以可以把 \(n\) 放在末尾。
考虑现在如何计算答案,我们可以把前缀最大值个数和后缀最大值个数分开考虑。考虑前缀最大值个数,那么考虑从 \(l\) 转移到 \(r+1\),那么即是 \([l,r]\) 的前缀最大值个数,那么 \(l\) 一定会产生贡献,然后 \(l\) 会找到第一个大于它的位置,把中间的弹掉,持续这个过程,也即是相当于一个单调栈。那么很显然我们只考虑从 \(l\) 转移到第一个大于它的位置即可,后面它也会自己处理掉。后缀最大值个数同理。
复杂度 \(\mathcal O(nk)\)。不知道为什么做不出来,可能因为我是一个纯sb吧😋😋😋
CF1325F Ehab's Last Theorem
Solution
我是shaber,什么都做不出来😂😂😂
我们首先在dfs tree上面考虑,如果返祖边有深度差 \(\ge \lceil\sqrt n\rceil\) 的,显然可以构成环,否则,一定会存在大小 \(\ge \lceil\sqrt n\rceil\) 的独立集,因为我们考虑dfs tree树上面从底往上选独立集,那么你选了一个点之后最多只会有 \(\lceil\sqrt n\rceil-1\) 个点不能选了。然后直接从底往上暴力选即可。
shaber tr真是一个什么都做不出来的好废物啊🤩🤩🤩
CF521E Cycling City
Solution
shaber 了,现在一看到无向图问题就想 tarjan😅😅😅
我们注意到在dfs树上一条树边如果被非树边覆盖两次就可以构造了,大概就是:
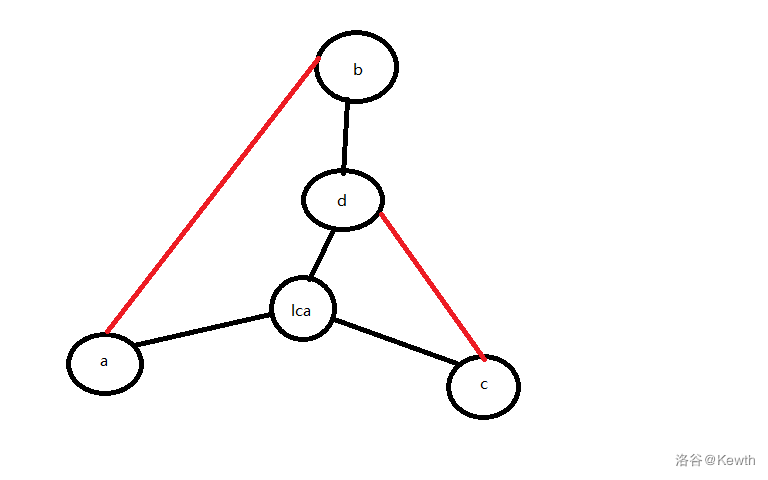
从 \(d\to \text{lca}\) 的路径就有 \(d\to \text{lca},d\to b\to a\to \text{lca},d\to c\to \text{lca}\),随便做一下就好了。
QOJ5357 芒果冰加了空气
Solution
不懂了,连sb题都搞不好了😥😥😥
我们注意到其实两个连通块如果分别确定了其分治顺序,其实它是可以合并的,假设连接节点是 \(u,v\),其分治树上的深度分别为 \(i,j\),那么其实相当于把长度为 \(i\) 的链和长度为 \(j\) 的链用一种顺序归并起来,别的并不关心。那么我们直接树上dp就可以做到 \(\mathcal O(n^2)\) 了。
CF804E The same permutation
Solution
完蛋了,什么都做不出来了😎😎😎
注意到 \(n\equiv 2,3\pmod 4\) 的时候是无解的,因为你交换一次逆序对奇偶性会变。然后我们发现可以每 \(4\) 个为一组,组内交换方案是可以搜出来的,而两个组之间交换不改变的方案也是可以搜出来的。直接做就好了。但是我做不出来🙂🙂🙂
CF1344F Piet's Palette
Solution
我是寸寸地飞屋😥😥😥
注意到可以赋成 \(0,1,2,3\),,比如空为 \(0\),R 为 \(1\),Y 为 \(2\),B 为 \(3\),然后一次混合就变成异或和。但是难点在于修改,但是我们考虑把二进制下两位拆开,分别设为 \(a,b\),那么 RY 就是交换 \(a,b\),RB 就是 \(a\to b\otimes a\),YB 就是 \(b\to a\otimes b\)。然后直接用 bitset 优化高斯消元即可。复杂度 \(\mathcal O(n^3/\omega)\) 。
CF1081G Mergesort Strikes Back
Solution
归并题能不能去死啊😮😮😮
发现就是相当于分成了 \(2^{k-1}\) 个段,段的长度只有 \(2\) 种,然后归并起来。我们注意到这个归并就相当于底层的一个块按前缀最大值分段之后把所有段按其开头排序之后放在一块。然后底层的一块内部逆序对数量是不会改变的。我们只需要考虑两个块之间的贡献。对于第一段的第 \(i\) 个数,和第二段的第 \(j\) 个数,当 \(a_i>a_j\) 且 \(i\) 的前缀最大值小于 \(j\) 的前缀最大值时会产生贡献,那么它的期望贡献就是 \(\dfrac{i+j-2}{2(i+j)}\),其实就是当 \(i,j\) 都不是前缀最大值的时候就有 \(\dfrac{1}{2}\) 的概率产生逆序对。
然后直接算一下就好了。但是我是shaber😌😌😌
lxl 的 sb 讲课
因为感觉思路比较统一,又懒得开新的,就放在这里了。😋😋😋
值域倍增分块
其实这个就是按 \([2^k,2^{k+1})\) 的形式分块,然后一个值不断下降经过的块只有 $\log $ 个。
CF1515I Phoenix and Diamonds
Solution
值域倍增分块的板子题目,但是我tm写了1个多小时的假算法😎😎😎
我们可以看出的是,我们值域分块之后,假设当前的 \(c\) 在 \([2^c,2^{c+1})\),我们如果碰到一个可删的值也在 \([2^c,2^{c+1})\) 里面,那么它一定会到下面的块去,否则我们会一直删在 \([1,2^c)\) 里面的值,直到它不在这个块里面。
我们考虑如何快速维护这个东西,可以发现的是如果我们最后是通过同一个块里面的值降到下面一个块,那么我们可以二分去找到它的位置,否则我们就一直用 \([1,2^c)\) 里面的值去消。我们如果写线段树二分的话就可以做到 \(\mathcal O(n\log^2 n)\)。直接在线段树上面操作会好写一点。
我果然不是代码实现大师😣😣😣
2019ICPC徐州 Yuuki and a problem
Description
给出一个长度为 \(n\) 的序列,有修改操作,以及询问一个区间子集和的 \(\text{mex}\) 。
\(n\le 2\times 10^5\)
Solution
一个显然的暴力的是,我们按值从小到大,假设当前的可表达范围是 \([0,x]\) ,当前考虑到了 \(z\),如果 \(z>x+1\) 那么答案就是 \(x+1\),否则 \(x\to x+z\) 。
我们还是考虑值域倍增,注意到假设 \(x+1\in [2^k,2^{k+1})\),如果 \([2^k,2^{k+1})\) 中的最小值 \(\le x+1\),那么该值域里面所有数显然都可以选到。那么直接用线段树维护一下就可以做到 \(\mathcal O(n\log^2 n)\) 了。
减半警报器
GYM 102331F Fast Spanning Tree
Solution
减半警报器的板子捏🤣🤣🤣
我们可以把 \(s\) 拆成两个 \(\lceil\frac{s}{2}\rceil\) 分别放在 \(u,v\) 上面,然后一次合并想到把两个集合上的值都减去另外一边集合的和。两个有任意一个减到 \(0\) 了之后就拿出来判一下,如果不合法就把剩下的部分接着这样拆分。
可以看出的是一个数最多被这样操作 \(\log s\) 次。我们用个数据结构维护就可以做到 \(\mathcal O(n\log n\log s)\) 了。应该没有sb去写线段树合并吧😅😅😅
第一类支配对
[Ynoi2006] rldcot
Solution
板子题目。注意到会产生贡献的点对只有在dsu on tree时一个点的前驱和后继,这意味着一共只有 \(\mathcal O(n\log n)\) 个点对。那么我们可以直接区间数颜色,大概就是 \(r\) 往右边扫,维护每个颜色最大的 \(l\),然后 BIT 算一下就好了。
复杂度 \(\mathcal O(n\log^2n+m\log n)\)。难得写到的小清新数据结构题。😊😊😊
第二类支配对
CodeChef Minimum Xor On Segment
Solution
显然有分块的 \(\mathcal O(n\sqrt n\log n)\) 的做法,但是过不了。
不过我们注意到有用的点对只有对于 \(x\) 二进制同一 \(\text{lcp}\) 最早出现的位置。因为如果同一个 \(\text{lcp}\) 会出现两个数的话显然把这两个数异或起来的答案会更优。然后还是区间数颜色的套路直接做就好了。
复杂度 \(\mathcal O(n\log^2n)\)。
[Ynoi2004] rpmtdq
Solution
又是难得的小清新题目捏🤩🤩🤩
我们还是支配对,发现在点分治的过程中对于一个点只需要找距离<它的编号的前驱和后继(距离指到分治中点的距离),这是因为,对于 \(x<y<z\),满足 \(\text{dis}_x,\text{dis}_y<\text{dis}_z\),那么很显然对于 \(x\) 而言 \(x\) 跟 \(y\) 匹配会更优秀。
但是sb lxl会卡常,所以不能用set,用个单调栈弹弹弹就好了😏😏😏
[NOI2013] 树的计数
Solution
妈妈生的题,nm不告诉我遍历顺序让我自己猜是吧😃😃😃
此题默认遍历时从小到大!!!。一个性质是,对于BFS序的一种合法划分它只会唯一对应一棵树。这个构造可以对于一层一层地考虑去在 dfs 序上面找到它所对应的父亲。我们考虑在 BFS 序上面的划分情况。考虑在 BFS 序上面相邻的两个点 \(x,y\),可以发现如果 \(\text{dfn}_x>\text{dfn}_y\),那么 \(x,y\) 之间是一定需要划分的。但是这样还不够。再考虑 DFS 序上面相邻的两个节点 \(x,y\),如果 \(\text{bfn}_x<\text{bfn}_y-1\),这说明 \(y\) 一定是 \(x\) 的儿子,而这也意味着 \([\text{bfn}_x,\text{bfn}_y]\) 的深度差 \(=1\),那么在之前也一定有位置钦定了划分,所以相当于这段区间不能再划分。注意到此时其它位置都是可划可不划的,贡献算 \(0.5\) 即可。
复杂度 \(\mathcal O(n)\)。
NowCoder 铬合金之声
Solution
我是shaber,套路题也做不来了,一直在想nm生成函数😅😅😅
其实就是有 \(n-m\) 个有根树,求方案数。我们考虑建出一个虚点,往每个树的根连,那么就是求这个的方案数。直接 prufer 序列算就好了,答案就是 \(\dbinom{n-1}{m}n^m\)。
似乎很多题都是这样,可以把一些东西结合起来,进而简化运算。
【UNR #3】百鸽笼
Solution
我是nm纯纯的飞屋🤩🤩🤩
我们考虑到其实题目相当于每次随机一个列,如果已经满了就不管,然后最后一个选完的是 \(i\)。可以发现这跟题目是等价的。那么我们可以设 \(G_i(x)=\sum_{k=0}^{a_i-1} \frac{x^k}{k!}\),我们设
那么对于 \(i\) 的答案就是:
(需要多确定一下最后一位,所以是 \(t+1\))
对于 \(F_k(x)\) 我们发现我们可以表示成 \(\sum_{i} \sum_{j} f_{i,j}x^i(e^x)^j\) 这种形式,而 \(f_{i,j}\) 是可以 \(\mathcal O(n^5)\) 处理出来的。问题就是如何快速计算 \(f_{i,j}\) 产生的贡献,发现其贡献为:
发现后面这个东西可以用广义二项式展开,那么就是:
然后就可以做了。复杂度 \(\mathcal O(n^5)\)。
「LOJ6737」指数公式
Solution
难死我了😫😫😫
我们注意到我们设
那么我们其实就是求 \(k![x^k]\exp F\)。但是问题就是在于这玩意是模 \(2\) 意义下进行的。直接阶乘肯定是没法算的。但是很显然可以根据 Lucas 定理把指数型生成函数乘法变为子集卷积。
我们的问题还是在于求 \(\exp F\)。考虑牛顿迭代法,那么我们就有:
(运算皆为子集卷积)
问题就在于我们如何求出 \(\ln G_0\)。发现即是求:\(\int 1/G_0\cdot G_0^{'}\)。一个事实是,当常数项为 \(1\) 的时候,在模 \(2\) 意义下 \(F\cdot F=1\),因为你交换子集和补集是合法的,那么就会一一对应,在模 \(2\) 意义下即为 \(0\)。因此,我们就是要求 \(\int G_0G_0^{'}\)。问题是这里的积分和求导怎么求,其实我们发现,我们维护的是类似于 \(s_i\cdot \dfrac{x^i}{i!}\),那么你求导只是变为了 \(s_i\cdot \dfrac{x^{i-1}}{(i-1)!}\),积分也是类似的道理。所以就是整体位移一下即可。那么我们就能直接算了。
不太巧妙的题目,但是思维难度很高。😥😥😥
CF527E Data Center Drama
Solution
不懂,2600 的题真的做了半个月都没有做出来😂😂😂
首先我们看出肯定是需要每个点度数都为偶数且总边数为偶数,然后你发现这时候肯定是有欧拉回路的,发现对于 \(a\leftrightarrow b\leftrightarrow c\leftrightarrow d\leftrightarrow ...\leftrightarrow a\) 的这种路径,我们可以直接构造:\(a\to b\gets c\to d\gets ...\gets a\)。所以直接把度数为奇数的点两两配对,如果边数为奇数就连个自环就好了。
关键是:在构造欧拉回路的时候我们需要先递归再加边,如果先加边再递归在环并环的时候是错的!!!
[ARC084F] XorShift
Solution
好久都没有做别的题了捏🤗🤗🤗
我们不难发现直接放在线性基里面然后查一下就好了,后面查答案的时候我还被卡了一会,其实就是跟数位dp是类似的,保存当前的值,看当前的限制,当可以拜托限制的时候后面的方案就可以随便选了。但是复杂度就爆炸了 ,即使用 bitset 优化也是\(\mathcal O(n|S|^3/\omega)\) 的。
注意到我们可以是把初始串的每种位移结果都加进去的,但是我们线性基其实不关心你插入了什么值,我们只关心可以表示出来的值,那么我们可以把上次的剩余串左移一位接着加入。发现这个时候你一个串最多进行 \(\mathcal O(|S|)\) 次操作,那么复杂度就是 \(\mathcal O(n|S|^2/\omega)\) 的了。
[ARC083F] Collecting Balls
Solution
做不出来捏😎😎😎
我们考虑将一个点 \((x,y)\) 视作 \(x\leftrightarrow y+n\) 的一条边,因为我们是一个机器人对应一个球,所以在这个图上面就是一个点会对应一条边。又因为总点数等于总边数,所以有方案的话一定是一个基环树森林,且定向方案只有两种,就是环上面的方向可以变化。
然后我们就需要考虑在我们确定了每个 🤖 对应了每个 ⚽ 之后如何计算答案。考虑到如果点 \((x,y)\) 交给A类 🤖 处理的话,那么 \((x^{'},y),x^{'}\not= x\) 就一定会交给一个 B类 🤖 处理,且对于对于 \((x^{'},y),x^{'}\),它被处理的时间必须在 \((x,y)\) 之前。B类 🤖 也是同理的。那么我们发现这玩意先后关系就是一个树,确定顺序其实就相当于给树确定了一个合法的 topo 序。这个的答案就是:
这个玩意可以归纳法证明。当然也可以不用这个用组合数硬算。
然后这个题目就做完了。感觉是挺套路的,不知道为什么做不出来捏🤣🤣🤣可能是脑子有点痛吧,但是想到建边之后就比较顺畅了。😋😋😋
CF1236F Alice and the Cactus
Solution
不懂为什么会做不出来,可能是没有沉下心来思考吧🤔🤔🤔
我们可以发现连通块数量=点数-边数+环数,我们不妨设为 \(a,b,c\),注意到我们其实是求 \(E(x^2)-E^2(x)\),问题就是在于求 \(E(x^2)\),也即是求 \(E((a-b+c)^2)=E(a^2)+E(b^2)+E(c^2)-2E(ab)+2E(ac)-2E(bc)\),以 \(E(c^2)\) 为例,那么也是求两个环同时存在的概率之和,发现两个环要么没有交点,要么只有一个交点,对于每个环分别计算与它有交的环的贡献以及没有交的环的贡献即可。别的也是同理。
还是不懂为什么会做不出来,或许是一直在想直接计算 \(E(x^2)\) 而没有考虑连通块数量与其他的关系。
[ARC089F] ColoringBalls
Solution
可以做的题,但是思维难度还是有点大了😣😣😣
我们考虑对于一个有颜色段怎么样才能构造出来,如果为 rrrrr,那么我们只需要一个 r 。如果为 rrrbbb..bbrrr,那么我们只需要一个 rb 即可,否则如果该段中连续的 b 段数量为 \(c\),那么我们需要 rb 再加上 \(c-1\) 个 b/r,比如 brb 我们就可以用 rbr 处理出来。
那么我们考虑枚举有 \(y\) 个纯 r 段以及 \(x\) 个有 b 的段。那么我们想要它合法的话,我们一定会先抽出最前面的 \(x\) 个 rb,然后再抽出 \(y\) 个 r,然后对于对于每个存在 b 的段去抽出 \(c-1\) 个操作,然后判断是否为空。我们用代数表示即为,将 \(c\) 从小到大排序后,设 \(\text{pos}_i\) 为在第 \(i\) 个 rb 中 b 的对应位置,\(\text{sum}_i\) 表示 \([i,n]\) 这段后缀中没有被选出的个数,就有:\({\text{sum}_{\text{pos}_i}}\ge \sum_{t=i}^{x} (c_t-1)\)。
有了上面的铺垫,那么我们就可以考虑如何 dp 了。我们可以设 \(f_{i,j,k}\) 表示按 \(c_{1,2,...,x}\) 从后往前考虑到第 \(i\) 个,\(\sum (c_t-1)=j\) 且 \(c_i=k\) 的方案数,那么我们就可以转移式:
可以发现这部分可以用前缀和优化做到 \(\mathcal O(n^3\log n)\)。
然后我们接着考虑如何计算最后的答案。首先我们把纯色段和有 b 段组合在一起,贡献为 \(\binom{x+y}{x}\),然后我们发现其实我们相当于球与小盒的问题了,比如一个有 \(c\) 个 b 段的有颜色段,那么相当于往 rbrbrbr...rbr 这 \(2c+1\) 个盒子里面放球,其中两边的 r 是可以不放的,而中间的 \(2c-1\) 个是必须得放得。然后还有我们中间必须要插入的 w,它也是必须要放球的,而我们在最左边和最右边放两个 w 段,它们也是不一定要放的。所以对于 \(\sum (c_t-1)=j\),那么我们就有 \(A=2j+2x+2y-1\) 个盒子必须放球,有 \(B=2x+2\) 个盒子可以不放球,那么它们的贡献就是 \(\binom{n+B-1}{A+B-1}\)。所以,我们的答案就是:
综上,我们可以 \(\mathcal O(n^5\log n)\) 解决这个问题。
麻烦死我了,看了一下午的题解😥😥😥
[ARC088E] Papple Sort
Solution
有教育意义的一个题目😏😏😏
我一开始的想法是我们不断把两边相同的抵消,对于不能抵消的,对于左端点,找到在另外一边离右端点最近的相同点,然后移动它们,在奇数长度的时候我们可以提前把需要移到中点的点移到中点然后这样处理。感觉是对的,但是很麻烦,所以没写捏🙄🙄🙄
另外一个有启发意义的思路是,我们可以考虑对于每个点确定它最后的位置,那么最小移动距离就是逆序对数量。首先对于相同字符出现的位置,它们的相对关系是不会变的,否则答案就不优,所以最后的匹配也就是确定的。另外,注意到的是对于 A...A...B...B 我们移动成 A...B...B...A 和移动成 B...A...A...B 的贡献是一样的,它们的逆序对都是 \(2\),那么让左端点配对的点移动到最右边最优。奇数的时候把无配对的点放中间即可。编完号直接求逆序对即可。
其实感觉上面的两种做法本质是相同的,但是第二种更简洁也更有启发性一点捏。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号