2020-08-03 集训题目题解
String Journey
题目大意
给出一个长度为\(n\)的字符串,求出最大的\(k\),使得可以在该字符串中选出\(k\)个子串,并且前一个子串包含后一个子串。
\(n\le 500000\)
思路
不难想到第\(i\)个子串(从后往前)的长度最优情况一定为\(i\)(显然)。于是,我们可以设\(dp[i]\)表示将\([i,i+dp[i]-1]\)作为第一个子串最大的\(k\)。然后,就有一种十分显然的\(\Theta(n^2)\)哈希做法。
这个时候,我们又发现\(dp[i]\le dp[i+1]+1\),大概原因见下图:
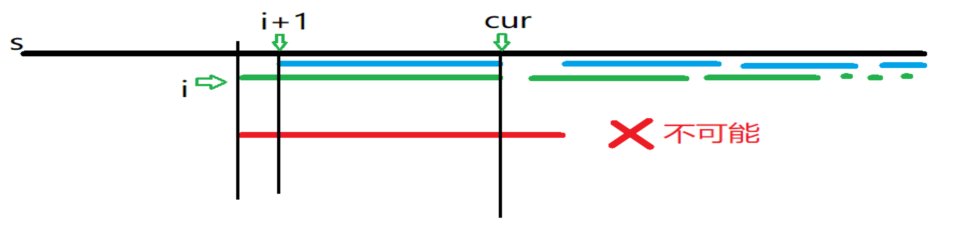
上面的\(\texttt{cur}\)就是\(i+dp[i+1]\)。
于是,我们只需要判断当前\(dp[i]\)对于当前\(i\)是否合法即可,时间复杂度就可以降为\(\Theta(nc)\),其中\(c\)为单次判断的时间复杂度。
其实我们可以将\(c\)优化到\(\log n\)。我们考虑\(dp[i]\)合法当且仅当存在\(j\)使得\(j\ge i+dp[i]\)并且\([j,j+dp[i]-2]\)为\([i,i+dp[i]-1]\)的后缀或者\([i+1,i+dp[i]]\)的前缀并且\(dp[j]\ge dp[i]-1\)。然后你就发现这个东西我们可以用后缀自动机加上线段树做。时间复杂度就降到了\(\Theta(n\log n)\)。
\(\texttt{Code}\)
Colorful Slimes
题目大意
有 \(n\) 个颜色的史莱姆,颜色为 \(1\to n\) 。每次可以花 \(A_i\) 的代价抓走一只史莱姆,或者是花费 \(x\) 的代价让剩余史莱姆的颜色+\(1\)(颜色为 \(n\) 的变为1)。
\(n\le 2\times 10^3\)
思路
水题。直接枚举一下颜色+\(1\)多少次即可。
时间复杂度\(\Theta(n^2)\)。
\(\texttt{Code}\)
Prefix Median
题目大意
对于一个排列\(a_{1,2,...,2n-1}\),我们可以对其构造数组\(b_{1,2,...,n}\),满足\(b_i=a_{[1,2i-1]}\)的中位数。
对于一个数组,求出它所有排列对应了多少种不同的构造数组。
\(n\le 50\),答案对\(10^9+7\)取模。
思路
我们首先可以看出两个事情:
-
\(b_n\)总是固定的。
-
\(b_i\)和\(b_{i+1}\)之间不会移动超过一位。
第一个显然,第二个也很显然,就是分类讨论一下就好了。
然后我们手玩一波发现,如果我们对\(a_{1,2,...}\)数组进行排序,那么,\(a_{i}\le b_i\le a_{2n-i}\)。这个其实就是第二个结论的推导结论。
我们还发现第二个结论还可以推出这样一个性质:
- 不存在\(i<j\)并且\(b_j<b_i<b_{j+1}\)或者\(b_{j+1}<b_i<b_j\)
于是,我们可以设\(f_{i,j,k}\)表示从后往前考虑到\(b_i\),有\(j\)个小于等于\(b_{i}\),有\(k\)个大于\(b_{i}\)。然后我们就很容易得到一个\(\Theta(n^4)\)的方法了。
\(\texttt{Code}\)
Salvage Robots
题目大意
给出\(n\times m\)的矩阵,上面有些格子有机器人。机器人可以且仅可以一起向上下左右移动,走出边界就死了,走到终点就活了。问最多可以救活多少台机器人。
\(n,m\le 100\)
思路
这道题首先有一个很妙的部分,就是我们不让机器人动,而是让终点动(如果大山不会走向穆罕默德,穆罕默德可以走向大山(bushi , 但是我们还有机器人掉下去的限制,于是我们还需要附加一个可以跟着终点动的框,在框外的机器人自动挂掉。
我们同时发现一个重要的性质,如图:
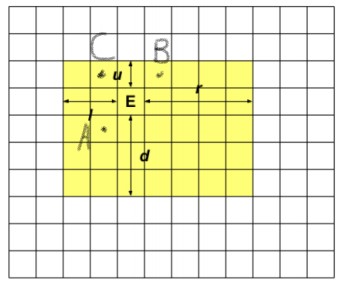
如果我们的终点已经走过\(A,B\),那么走到\(C\)不是使答案变劣。(应该很显然吧。。。)
于是,我们可以考虑设\(f_{i,j,k,l}\)表示终点走完以\((i,j)\)为左上端点\((k,l)\)为右下端点的矩形可以救到的最多的机器人。然后我们可以考虑往四周拓展。不过细节似乎有点多。。。
\(\texttt{Code}\)
Cleaning
题目大意
给出一个\(n\)个点的树,每个点有\(a_i\)个石头,每次可以选两个叶子把该路径上所有节点拿掉一个石头,前提是路径上不能有节点没有石头。问是否可以让每个节点都没有石头。
\(n\le 10^5\)
思路
应该不是很难吧?只是细节有点多(虽然并没有上面几道题多
不难想到设\(f_u\)表示从\(u\)子树中能够往外延伸的石子个数,再设\(s_u=\sum_{v\in son_u} f_v\),那么我们可以得到:
应该很好理解吧(手动划掉)
于是,我们移项得到:
那么判断方法就是是否\(\forall u,0\le f_u\le a_u\)并且\(f[root]=0\)(\(root\)就是根)还有\(\max_{v\in son_u}f_v \le a_u\)。
可能最后一个比较难理解,这里解释一下,大概意思就是如果两两匹配有一个过大就不得行,即\(\max_{v\in son_u} f_v-f_u>a_u-\max_{v\in son_u}f_v\),然后移项得到这个式子。
于是我们就可以在\(\Theta(n)\)的时间复杂度内解决这个问题了。(注意特判\(n=2\)的情况)
\(\texttt{Code}\)
New Year and Arbitrary Arrangement
题目大意
给出\(k,pa,pb\),表示有一个ab字符串,每次有\(\dfrac{pa}{pa+pb}\)的概率添加一个a,有\(\dfrac{pb}{pa+pb}\)的概率添加一个b,但是一旦ab子序列大于等于\(k\)就立马停止。问最后字符串里面ab子序列的期望个数。
思路
因为一个错误翻译让我理解不了题解。。。说明yybyyb是个屑(划掉)
为了方便,下面设\(A=\dfrac{pa}{pa+pb},B=\dfrac{pb}{pa+pb}\)
我们发现有无数种终止状态。。。真的很恶心了。。。(更何况我期望dp菜得一批)但是其实我们还是可以做的,我们可以设\(f_{i,j}\)表示当前有\(i\)个a,\(j\)个ab子序列,结束时的ab子序列的期望个数。
我们可以列出转移方程:
考虑边界情况\(i+j\ge k\)的情况,这个时候我们只要再出现一次b就可以结束这个游戏,于是答案就是\(i+j+k\),其中
这个东西用错位相减可以求出来等于\(\dfrac{pa}{pb}\)。
于是,我们就可以\(\Theta(k^2)\)解决这个问题。
一个小细节就是,我们最后的答案不能取\(f_{0,0}\)而要取\(f_{1,0}\),因为\(f_{0,0}\)会对自己不听产生贡献,换句话说就会陷入bbbbb...bbbba...无限个b这种情况,但是我们发现第一个a之前的b其实都是没有什么用的(社会渣滓(大雾 ,于是答案就可以取\(f_{1,0}\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号