常用损失函数 LossFunction

文章结构

1. 损失函数在神经网络中的位置
2. 常用的损失函数（结构：解释，公式，缺点，适用于，pytorch 函数）
   1. MAE/L1 Loss
   2. MSE/L2 Loss
   3. Huber Loss
   4. 对信息量、熵的解释
   5. relative entropy 相对熵/ Kullback-Leibler KL Loss 
   6. Cross Entropy Loss 交叉熵（包含对softmax 层的解释）
   • 相对熵、熵、和交叉熵的关系
   7. Hinge Loss

 

 

 

损失函数在神经网络中的位置

forward → loss → backward

 

 

 

常用的损失函数

 

 

 

 

信息量

由香农引入，可以理解为对事件X发生概率的估计。一件事越经常发生，就越容易预测，它所包含的信息量就越小。

公式：

其中，  表示信息量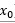，表示事件X中的一个种类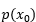， 表示该种类的概率分布。

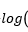取对数  是为了方便计算，接下来都用简写代替。

熵

每个种类的发生概率与信息量的乘积和，表示一个系统不确定性或混乱程度。

对于系统的不确定性可以理解为，由概率分布计算得到的信息量越大，表示越不容易预测，同时意味着并不遵循一定的规律，越混乱/不确定。

公式：

 

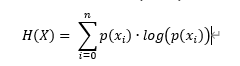
 其中 ，表示熵，求和上标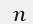表示事件X的种类/分类的个数（举例，掷硬币这一事件的种类有正、反2种）， 表示第i种类的概率分布。

 

 

relative entropy 相对熵/ Kullback-Leibler KL Loss 

、 为 事件X 中取值的两个概率分布， 对 的相对熵（≥ 0 ）：

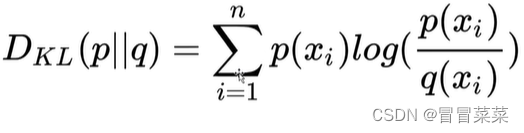
公式引用自：http://t.csdnimg.cn/hRb5X

这里的两个概率分布可以是（由标签/target 计算得到的）真实概率和模型预测概率。

在pytorch 官方文档中 KLDivLoss — PyTorch 2.3 documentation 解释为

 

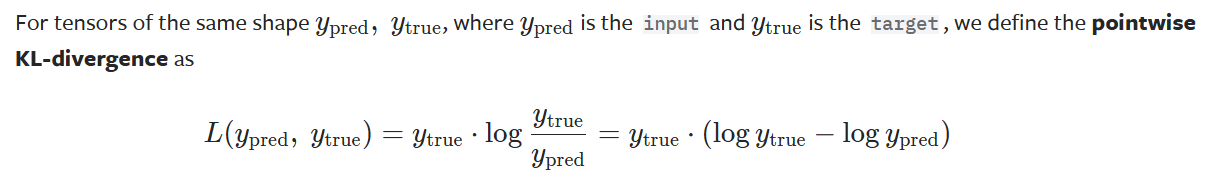
pytorch 函数：

 

 

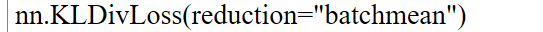
Cross Entropy Loss 交叉熵

公式：

 

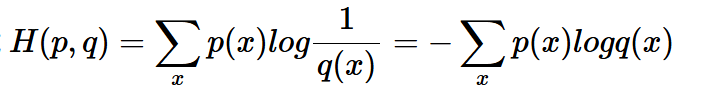
表示 真实概率和预测概率的差距。

公式引用自详解机器学习中的熵、条件熵、相对熵和交叉熵 - 遍地胡说 - 博客园 (cnblogs.com)

 

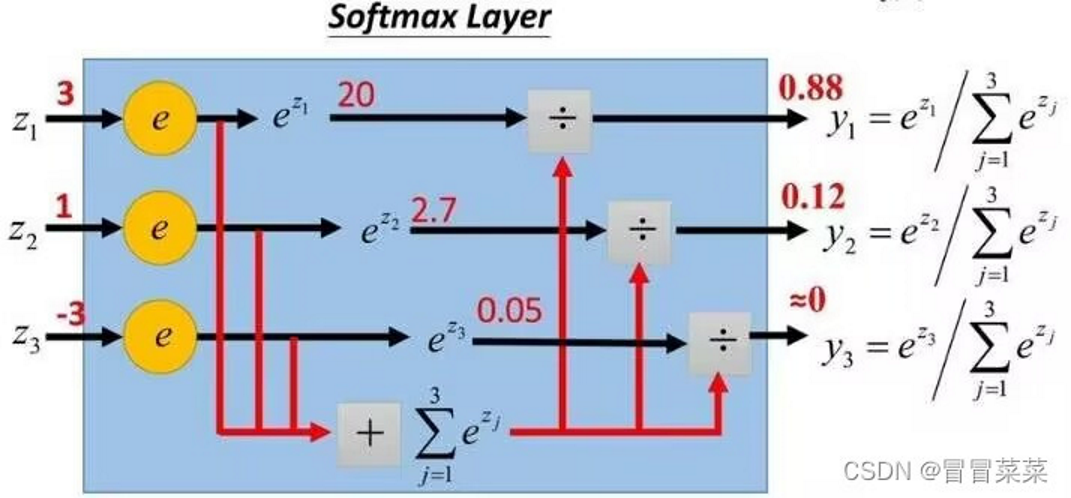
其中， 在实际运用中，由 softmax 层 计算得到 。

 

Softmax 层输出的是每个分类的概率分布，将数字转化为概率。

 引用：http://t.csdnimg.cn/hRb5X

在pytorch 官方文档中，其中 是一个1D 的张量，为每个类别分配权重，C 为事件的分类总数，相当于上文中的n。

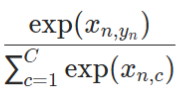为softmax的输出。

 

 

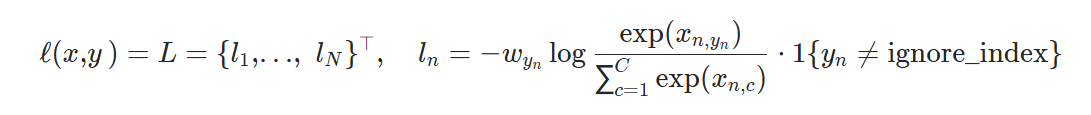
适用于：分类；样本分布不平衡的训练集

pytorch 函数：

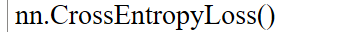
 其中，官方文档解释，input不需要normalize。