自然语言处理 - 词向量

词向量

在自然语言处理（NLP）中，词向量将单词按照含义编码成向量，从而更好地进行语言建模和特征学习。词向量经常作为下游 NLP 任务的基本组件，出现在文本分类、翻译、问答、推荐等各种任务模型中；此外，我们也可以通过多种方式，训练自己的词向量。（for more, see here）

通过本次实验，你将进一步体会词向量的特性，以及词向量模型的加载使用。

实验环境

你可以使用任何你自己熟悉的 python 环境来完成实验，我们提供了 conda 环境配置文件 environment.yml，里面给出了一些必要的环境依赖，请确保你安装了这些依赖。如果你需要使用其他 python 扩展包可自行安装。（本次实验二所需的环境依赖在实验一的环境中都有，因此你也可以跳过下面的虚拟环境创建步骤，直接启用实验一的环境进行实验。）

这里我们推荐使用 conda 来创建管理 python 虚拟环境。

  1. 下载安装 conda。你可以选择安装已经预装了许多常用扩展的 Anaconda 或者没有任何预装的 Miniconda。

  2. 打开 Terminal（Windows 可使用 Anaconda Prompt） 并进入当前文件目录，输入以下命令来创建一个名为 nlplab2 的虚拟环境并启用。

conda env create -f environment.yml
conda activate nlplab2
  1. 使用 jupyter-notebook 打开 lab2.ipynb 文件开始下面的实验。
jupyter-notebook lab2.ipynb

实验过程

加载词向量

加载预训练好的词向量。这里我们使用 GLoVe 在中文维基百科语料训练的词向量，词向量维度为 50，词汇量 83W+。为了减少后续的计算时间，我们使用 pickle 模块将词向量模型保存到二进制文件，你可以在 data 目录下看到它。运行下面的代码加载处理后的 50 维词向量。

Notes：

  • 选择 GLoVe 词向量是由于它在词语类比任务上有着更优的特性。
  • GloVe 官网 提供的都是英文的预训练词向量，中文词向量需要自己用语料库训练。具体需要你到维基中文下载网页 zhwiki 下载中文维基百科语料 xml 文件；完成解析抽取、繁体化简、符号停用词过滤、分词等相关处理；下载 GloVe 官方源码 编译预训练。
  • 此处无需你完成整个词向量训练过程，我们已替你训练好，直接加载即可。
import pickle
import numpy as np

with open('data/glove.zh.50.pickle', mode='rb') as f:
    word2vec_map = pickle.load(f)
word2index = dict(zip(word2vec_map.keys(), range(len(word2vec_map))))
index2word = dict(zip(word2index.values(), word2index.keys()))
word_matrix = np.array(list(word2vec_map.values()))
del word2vec_map
print('len(word2index):', len(word2index))
print('len(index2word):', len(index2word))
print('word_matrix.shape:', word_matrix.shape)

len(word2index): 831144
len(index2word): 831144
word_matrix.shape: (831144, 50)

这里我们得到三个变量：

  • word2index：一个字典，以词（str）为 key，以一个 [0, 831144) 间的整数（int）为 value，词语到下标的映射；
  • index2word：一个字典，以 [0, 831144) 间的整数（int）为 key，以对应的词（str）为 value，下标到词语的映射；
  • word_matrix：一个维度为 (831144, 50) 的 numpy.ndarray 矩阵，第 i 行为下标为 i 的词对应的词向量。
    因此，一个词语 word 的词向量可以通过 word_matrix[word2index[word]] 取得，例如：
word_matrix[word2index['中科大']]

array([ 0.476694,  0.012429,  1.334308,  0.833337,  0.422843,  0.404001,
       -0.286563,  0.277617,  0.78868 ,  0.235541,  0.119859,  0.210273,
       -0.294097, -0.157735,  0.008777,  0.902468, -0.244504,  0.116923,
        0.847188, -0.549439,  0.086888, -0.533772, -0.649807, -0.1344  ,
        0.6017  , -0.178695, -0.423312, -0.3307  ,  0.364139, -0.012755,
        0.011284,  0.570228,  0.600845,  0.154449, -0.293372,  0.421692,
        0.274871,  0.700706, -0.160058,  0.345218, -1.173997, -0.345282,
       -0.490619, -0.787566,  0.912973, -0.113094,  0.091646, -0.316972,
        0.962285,  0.372473])

one-hot编码就是保证每个样本中的单个特征只有1位处于状态1，其他的都是0。独热编码即 One-Hot Encoding，又称一位有效编码，其方法是使用N位状态寄存器来对N个状态进行编码，每个状态都由他独立的寄存器位，并且在任意时候，其中只有一位有效。one-hot向量将类别变量转换为机器学习算法易于利用的一种形式的过程，这个向量的表示为一项属性的特征向量，也就是同一时间只有一个激活点（不为0），这个向量只有一个特征是不为0的，其他都是0，特别稀疏。

相比较于词的独热编码向量，fastText，GloVe等词向量包含有更多的信息，也可以更好的表达不同词语间的相似关系。

下面我们来看看如何使用这些词向量来计算两个词语间的相似程度。

余弦相似度（Cosine Similarity）

为了衡量两个词语间的相似程度，我们需要一种合适的计算两个向量间相似程度的方法。给定两个向量 \(\mathbf{u}\) 和 \(\mathbf{v}\)，余弦相似度定义为：

\[\text{CosineSimilarity}(\mathbf{u}, \mathbf{v}) = cos(\theta) = \frac{\mathbf{u} \cdot \mathbf{v}}{\|\mathbf{u}\| \|\mathbf{v}\|} = \frac{\sum_{i=1}^d u_i v_i}{\sqrt{\sum_{i=1}^d u_i^2} \sqrt{\sum_{i=1}^d v_i^2}} \]

其中 \(\mathbf{u} \cdot \mathbf{v}\) 为两个向量 \(\mathbf{u}\) 和 \(\mathbf{v}\) 间的点积，\(\theta\) 为两个向量 \(\mathbf{u}\) 和 \(\mathbf{v}\) 间的夹角，\(\|\mathbf{u}\|\) 是向量 \(\mathbf{u}\) 的 L2 范数，\(d\) 为向量的维数。

余弦相似度的大小取决于两个向量间的夹角的大小，如果 \(\mathbf{u}\) 和 \(\mathbf{v}\) 非常相似余弦相似度的值就非常接近1。

下面请你来实现函数 cosine_similarity 用以计算向量间的余弦相似度。

注意，上面公式给出的是两个向量间余弦相似度的计算过程，也可以认为是一个样本间的计算，即向量 \(\mathbf{u}\) 和向量 \(\mathbf{v}\) 计算得到一个浮点数结果 \(w\)。但为了后续可以进行快速的并行计算，这里要求你的实现可以进行批量处理，即多个不同的向量 \(\mathbf{u}\) 组成的矩阵 \(\mathbf{U} \in \mathbb{R}^{m \times d}\) 和多个不同的向量 \(\mathbf{v}\) 组成的矩阵 \(\mathbf{V} \in \mathbb{R}^{n \times d}\) 计算的到一个结果矩阵 \(\mathbf{W} \in \mathbb{R}^{m \times n}\)，结果矩阵 \(\mathbf{W}\) 的第 \(i\) 行第 \(j\) 列的数值 \(w_{ij}\) 为矩阵 \(\mathbf{U}\) 的第 \(i\) 行向量 \(\mathbf{u}_i\) 和矩阵 \(\mathbf{V}\) 的第 \(j\) 行向量 \(\mathbf{v}_j\) 的余弦相似度值。

Assignment Notes:

  • 仔细阅读下面几个 numpy 函数的说明文档，这些函数可能对你有帮助：

  • 如果你对 numpy 的广播（Broadcasting）机制不了解，可以参阅这些资料：

  • 为了保证你的实现是向量化的批量运算，请不要使用任何 for 循环来逐项计算。合理使用上面参考资料中的方法你可以只用一行代码就完成计算。

def cosine_similarity(u, v):
    '''
    计算向量间的余弦相似度。

    Args:
        u (numpy.ndarray): 维度为(m, d)的矩阵；
        v (numpy.ndarray): 维度为(n, d)的矩阵。

    Returns:
        (numpy.ndarray): 维度为(m, n)的矩阵，此矩阵第i行第j列的数值为矩阵u的第i行
            和矩阵v的第j行这两个向量依据上面的定义计算出的余弦相似度。
    '''
    ###### 开始 ######
    
    ### np.dot 求点积
    ### np.linalg.norm 求范数
    
    a = u
    b = v.T
    c = np.dot(a,b)
    d = np.linalg.norm(a,ord=2,axis=1,keepdims=True)
    e = np.linalg.norm(b,ord=2,axis=0,keepdims=True)
    mm = np.dot(d,e)
    return np.divide(c,mm)
    ###### 结束 ######

运行下面的测试，你应该得到如下结果：

mat1.shape: (3, 50)
mat2.shape: (2, 50)
mat3.shape: (3, 2)
array([[0.73747626, 0.3755256 ],
       [0.68657858, 0.40745768],
       [0.13122132, 0.75253873]])

father1 = word_matrix[word2index['爸爸']]
mother1 = word_matrix[word2index['妈妈']]
school1 = word_matrix[word2index['学校']]

father2 = word_matrix[word2index['老爸']]
school2 = word_matrix[word2index['校园']]

mat1 = np.array([father1, mother1, school1])
mat2 = np.array([father2, school2])
print('mat1.shape:', mat1.shape)
print('mat2.shape:', mat2.shape)

mat3 = cosine_similarity(mat1, mat2)
print('mat3.shape:', mat3.shape)
mat3

mat1.shape: (3, 50)
mat2.shape: (2, 50)
mat3.shape: (3, 2)





array([[0.73747626, 0.3755256 ],
       [0.68657858, 0.40745768],
       [0.13122132, 0.75253873]])

可以看到，这个例子中结果矩阵第1行第1列（“爸爸”和“老爸”的相似度）以及第3行第2列（“学校”和“校园”相似度）都有相对较高的余弦相似度数值。

最相似的词语

有了词向量间相似度的度量方法，我们便可以看看与某个词最相似的词语都有哪些。下面请你来实现 top_n_similarity 函数，给定一个词，返回与其最相似的 n 个词及其相似度。任意一个词一定和它自己是最相似的，请将自身排除在外。

Assignment Notes:

  • 想想如何充分利用你上面实现的可进行高效批量运算的 cosine_similarity 函数；
  • 仔细阅读下面的 numpy 函数的说明文档，这些函数可能对你有帮助：
  • 实现合理的话单次调用用时应该在数秒钟，甚至不到1秒钟。
def top_n_similarity(word, n, word2index, index2word, word_matrix):
    '''
    给定一个词，依据词向量间的余弦相似度找到与其最相似的前n个词并返回。

    Args:
        word (str): 给定的词；
        n (int): 需要返回的最相似词的个数；
        word2index (dict[str, int]): 词语到下标的映射；
        index2word (dict[int, str])：下标到词语的映射；
        word_matrix (numpy.ndarray)：词向量组成的矩阵。

    Returns:
        (dict[str, float]): 找到的n个词及其相似度，一个以词为key，以相似度为
            value的字典。
    '''
    if word not in word2index:
        raise ValueError('Word {} not in the vocabulary.'.format(word))
    ###### 开始 ######
    
    mydict=dict()
    #取出该单词的词向量，并转换为1维向量
    word1 = word_matrix[word2index[word]]
    mat1 = np.array([word1])
    #mat1 = np.expand_dims(word1,axis=0)
    
    #用该向量与原词组方程求相似度，得到该单词与所有词的相似度向量
    ans=cosine_similarity(mat1,word_matrix)
    
    #对该向量进行排序，得到其下标排序结果
    ans1=np.argsort(-ans)
    
    #将向量降维成数组
    ans=np.squeeze(ans)
    ans1=np.squeeze(ans1)
    
    for i in range(n):
        mydict[index2word[ans1[i+1]]]=ans[ans1[i+1]]
    return mydict
    
    ###### 结束 ######

运行下面的测试，你应该得到如下结果：

{'维也纳': 0.8026402573563235,
 '柏林': 0.789617648409123,
 '法国巴黎': 0.788222576783984,
 '法国': 0.783072750843146,
 '布鲁塞尔': 0.7728576184665334,
 '里昂': 0.7655693234781406,
 '伦敦': 0.76422517970406,
 '斯特拉斯堡': 0.7464075209702475,
 '日内瓦': 0.7349832595389842,
 '路易': 0.7206136726368307}

%%time
top_n_similarity('巴黎', 10, word2index, index2word, word_matrix)

Wall time: 651 ms





{'维也纳': 0.8026402573563235,
 '柏林': 0.7896176484091229,
 '法国巴黎': 0.7882225767839838,
 '法国': 0.7830727508431462,
 '布鲁塞尔': 0.7728576184665333,
 '里昂': 0.7655693234781408,
 '伦敦': 0.7642251797040602,
 '斯特拉斯堡': 0.7464075209702475,
 '日内瓦': 0.7349832595389842,
 '路易': 0.7206136726368307}

下面请发挥你的想象，任意选取你感兴趣的词语，看看哪些词与它相似，以及返回的结果是否合理。英文请使用小写。

word = '太阳'
top_n_similarity(word, 10, word2index, index2word, word_matrix)

{'地球': 0.8346179490851815,
 '金星': 0.8221919998313647,
 '星': 0.8163960486983992,
 '月亮': 0.8154737751842294,
 '天空': 0.7928664125367684,
 '行星': 0.750207872730994,
 '火星': 0.7497908278425455,
 '一颗': 0.746478634718834,
 '宇宙': 0.7345393772157445,
 '星星': 0.7298035233569619}

词语类比任务（Word Analogy Task）

在词语类比任务中，我们要完成类似这样一个任务：a 对于 b 相当于 c 对于____。举例来说，我们要完成一句话，巴黎对于法国相当于北京对于____？

巴黎与法国两个词之间是有语义关系的，巴黎是法国的首都，那么根据第三个词北京，我们可以推断出空白处应该填中国。

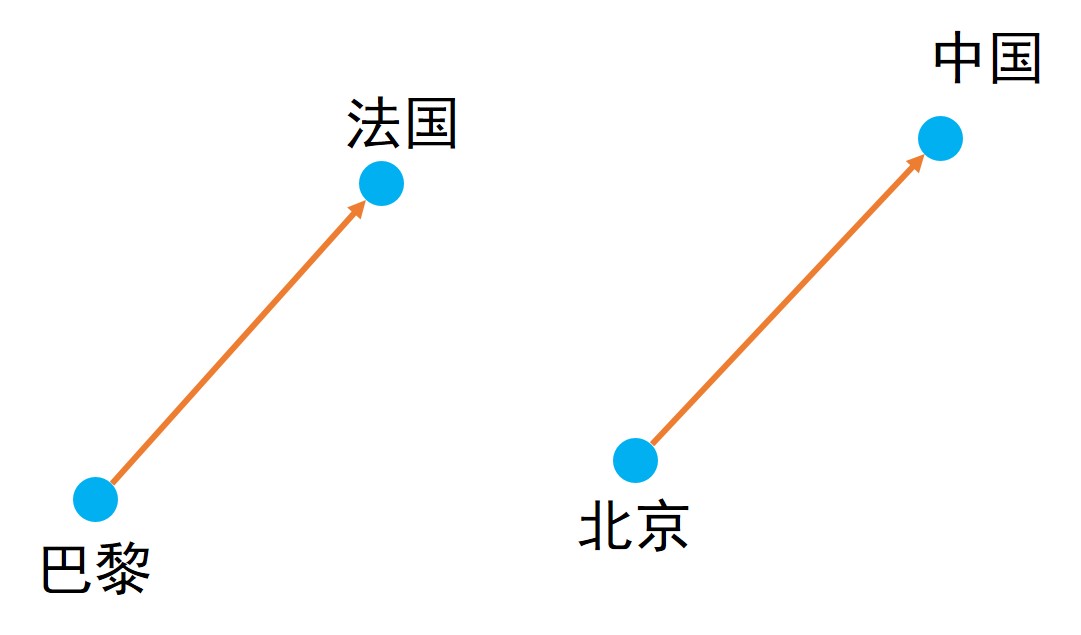
cDOmfx.jpg

根据上图中的关系我们可以得到：

\[\mathbf{v}_{法国} - \mathbf{v}_{巴黎} \approx \mathbf{v}_{中国} - \mathbf{v}_{北京} \]

即：

\[\mathbf{v}_{法国} - \mathbf{v}_{巴黎} + \mathbf{v}_{北京} \approx \mathbf{v}_{中国} \]

因此，对于我们需要找到，a 对于 b 相当于 c 对于____这样一个任务，我们需要找到最适合的 \(d\) 使 \(\mathbf{v}_b - \mathbf{v}_a + \mathbf{v}_c\) 和 \(\mathbf{v}_d\) 的相似度最高。这里我们同样使用余弦相似度来进行相似性度量。即：

\[d = \underset{w \in \mathbb{V}}{\mathrm{arg\,max}} \, \, \text{CosineSimilarity}(\mathbf{v}_b - \mathbf{v}_a + \mathbf{v}_c, \mathbf{v}_w) \]

其中 \(\mathbb{V}\) 为整个词汇表。

下面需要你来实现 complete_analogy_task 函数并用它来完成词语类比任务。该函数接受词语 a, b, c 为参数，返回相似度最高的 d，同时还有以下要求：

  • 为了方便分析与理解，这里要求函数返回相似度最高的前3个候选词及其相似度。
  • 我们不希望返回的词是 a, b, c 三个词本身，但有时候计算得到的相似度最高的前几个候选词中可能有 a, b, c 三者中的一个或几个，因此请将 a, b, c 三个词本身排除在外。

Assignment Notes:

  • 如果将 \(\mathbf{v}_b - \mathbf{v}_a + \mathbf{v}_c\) 当作一个词语的词向量，这里需要做的和 top_n_similarity 是很相似的。
def complete_analogy_task(
    word_a, word_b, word_c, word2index, index2word, word_matrix
):
    '''
    完成词语类比任务。给定已知的三个词 a, b, c，找到最适合的3个候选词 d 使得
    (v_b - v_a) 和 (v_d - v_c) 间的余弦相似度最小。

    Args:
        word_a (str): 词语 a；
        word_b (str): 词语 b；
        word_c (str)：词语 c；
        word2index (dict[str, int]): 词语到下标的映射；
        index2word (dict[int, str])：下标到词语的映射；
        word_matrix (numpy.ndarray)：词向量组成的矩阵。

    Returns:
        (dict[str, float]): 最合适的3候选词，以词为key，以相似度为value。
    '''
    for word in (word_a, word_b, word_c):
        if word not in word2index:
            raise ValueError(
                'Word {} not in the vocabulary.'.format(word)
            )
    ###### 开始 ######
    
    mydict= dict()
    wordlist =[]
    #取出该单词的词向量，并转换为1维向量
    word1 = word_matrix[word2index[word_a]]
    word2 = word_matrix[word2index[word_b]]
    word3 = word_matrix[word2index[word_c]]
    wordlist.append(word_a)
    wordlist.append(word_b)
    wordlist.append(word_c)
    mat1 = np.array([word2-word1+word3])
    
    #用该向量与原词组方程求相似度，得到该单词与所有词的相似度向量
    ans=cosine_similarity(mat1,word_matrix)
    
    #对该向量进行排序，得到其下标排序结果
    ans1=np.argsort(-ans)
    
    #将向量将维成数组
    ans=np.squeeze(ans)
    ans1=np.squeeze(ans1)
    
    k=0
    for i in range(6):
        p=index2word[ans1[i]]
        if p not in wordlist:
            mydict[p]=ans[ans1[i]]
            k+=1
            if(k==3):
                break
    return mydict
    
    ###### 结束 ######

运行下面的测试用例，你应该得到：

"巴黎":"法国" = "北京":"中国" 	前3候选: {'中国': 0.9035901571740452, '上海': 0.7863853529317479, '中华人民共和国': 0.7673241689100596}
"法国":"巴黎" = "中国":"北京" 	前3候选: {'北京': 0.8777837078974607, '上海': 0.7822645566195217, '杭州': 0.7708022456031641}
"北京":"中国" = "东京":"日本" 	前3候选: {'日本': 0.9126536930088033, '概要': 0.8140997356991334, '条目': 0.7620412947366628}
"哥哥":"爸爸" = "姐姐":"妈妈" 	前3候选: {'妈妈': 0.9105166131659955, '爱上': 0.8414034985959645, '我家': 0.8085360695344918}
"man":"king" = "woman":"queen" 	前3候选: {'queen': 0.7812693110741713, 'princess': 0.7761106573413572, 'lady': 0.7394024785261167}
"man":"男人" = "woman":"女人" 	前3候选: {'女人': 0.8282728834284955, '爱上': 0.7446765414784068, '漂亮': 0.7270981887885872}
"夏天":"summer" = "冬天":"winter" 	前3候选: {'winter': 0.827960010826369, 'spring': 0.8133394777339396, 'nights': 0.7302998615344509}
"猫":"cat" = "狗":"dog" 	前3候选: {'dog': 0.673225726288403, 'bell': 0.6685053095960879, 'avbe': 0.6440587722819132}

def show_cases(cases):
    for case in cases:
        result = complete_analogy_task(*case, word2index, index2word, word_matrix)
        print('"{}":"{}" = "{}":"{}"'.format(
            case[0], case[1], case[2], list(result.keys())[0]
        ), '\t前3候选:', result)

test_cases = [
    ('巴黎', '法国', '北京'),
    ('法国', '巴黎', '中国'),
    ('北京', '中国', '东京'),
    ('哥哥', '爸爸', '姐姐'),
    ('man', 'king', 'woman'),
    ('man', '男人', 'woman'),
    ('夏天', 'summer', '冬天'),
    ('猫', 'cat', '狗'),
]
show_cases(test_cases)

"巴黎":"法国" = "北京":"中国" 	前3候选: {'中国': 0.9035901571740453, '上海': 0.7863853529317478, '中华人民共和国': 0.7673241689100596}
"法国":"巴黎" = "中国":"北京" 	前3候选: {'北京': 0.8777837078974606, '上海': 0.7822645566195219, '杭州': 0.7708022456031642}
"北京":"中国" = "东京":"日本" 	前3候选: {'日本': 0.9126536930088031, '概要': 0.8140997356991332, '条目': 0.7620412947366628}
"哥哥":"爸爸" = "姐姐":"妈妈" 	前3候选: {'妈妈': 0.9105166131659955, '爱上': 0.8414034985959644, '我家': 0.8085360695344919}
"man":"king" = "woman":"queen" 	前3候选: {'queen': 0.7812693110741713, 'princess': 0.7761106573413571, 'lady': 0.7394024785261168}
"man":"男人" = "woman":"女人" 	前3候选: {'女人': 0.8282728834284955, '爱上': 0.7446765414784068, '漂亮': 0.7270981887885872}
"夏天":"summer" = "冬天":"winter" 	前3候选: {'winter': 0.827960010826369, 'spring': 0.8133394777339394, 'nights': 0.7302998615344509}
"猫":"cat" = "狗":"dog" 	前3候选: {'dog': 0.673225726288403, 'bell': 0.668505309596088, 'avbe': 0.6440587722819131}

下面请发挥你的想象尝试不同的例子，看看你是否可以得到合理的结果。请至少测试10个例子，英文请使用小写。

your_test_cases = [
    ('苹果', 'mac', '微软'),
    ('nba', '篮球', 'nfl'),
    ('四川', '火锅', '北京'),
    ('爷爷', '奶奶', '外公'),
    ('爷爷', '奶奶', '爸爸'),
    ('c', '编译', 'python'),
    ('英语', 'english', '数学'),
    ('王子', '公主', '男'),
]
show_cases(your_test_cases)

"苹果":"mac" = "微软":"windows" 	前3候选: {'windows': 0.8910806551309494, 'microsoft': 0.8529114256029701, 'xp': 0.8379023732611227}
"nba":"篮球" = "nfl":"排球" 	前3候选: {'排球': 0.7005484502888687, '橄榄球': 0.6665796989079577, '垒球': 0.6358227473678834}
"四川":"火锅" = "北京":"双合盛" 	前3候选: {'双合盛': 0.5892615817795352, '李太白': 0.5601195437064146, '汉堡': 0.5514640741701642}
"爷爷":"奶奶" = "外公":"姑姑" 	前3候选: {'姑姑': 0.7294645937903153, '外婆': 0.7193083976760439, '洪贞恩': 0.7190164658997995}
"爷爷":"奶奶" = "爸爸":"妈妈" 	前3候选: {'妈妈': 0.8551136273568736, '爱上': 0.847611952873073, '老公': 0.8176522434879868}
"c":"编译" = "python":"perl" 	前3候选: {'perl': 0.7076964643456336, 'zodb': 0.6825362384237011, 'cweb': 0.6784671475955981}
"英语":"english" = "数学":"mathematics" 	前3候选: {'mathematics': 0.757443123039894, 'mathematical': 0.6710243658734777, '高等数学': 0.6644685799868281}
"王子":"公主" = "男":"女" 	前3候选: {'女': 0.8330239176078883, '女主角': 0.7256086005422543, '嫁': 0.702171130631091}
posted @ 2021-04-12 22:47  Dallas98  阅读(397)  评论(1)    收藏  举报
蜀ICP备20020397号