2.Median of Two Sorted Arrays

4.寻找两个正序数组的中位数

leecode题目

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
Example：
输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

Example1：
输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

题解

第一种 我们新手先不考虑题目要求的时间复杂度去思考（常规思路，时间复杂度是O(m+n）)：就是把两个正序数组合并成一个正序数组，然后取出中位数。合并有序数组操作是 O(m+n)

第二种就是 按照题目要求时间复杂度为O(log（m+n）)，看到题目给的log的时间复杂度我们联想到二分搜索。

• 由于要找到最终的数组中位数，两个数组的总大小，中间位置都是可以知道的，所以我们能不能不合并两个数组就能获得中位数呢？答案是可以的，我们用二分搜索一个数组中切分的位置，里一个数组切分的位置也可以得到，然后在通过两个切分位置以及总长度是奇数还是偶数来得到中位数。为了使复杂度最小，所以二分搜索两份数组中长度最小的那个数组。
• 如何解决切分两个数组。我们假设这两个数组为nums1和nums2，其中nums1长度最小，我们就切分nums1. 首先二分得到nums1的切分线mid1。切分的线如何切分并满足中位数的条件呢？就是 线的左边的数都小于右边的数。 转换成一有序数组的代码就是 arr[mid-1]<=arr[mid]就说明左边的数都小于右边的数。 在转化成两组有序数组就是满足nums1[mid1-1]<=nums2[mid2] && nums2[mid2-1]<=nums1[mid1]这就说明左边的数都小于右边的数了. 不满足切分线就需要移动切线，如果nums1[mid1] < nums2[mid2-1]，说明 midA 这条线划分出来左边的数小了，切分线应该右移；如果 nums1[mid1-1] > nums2[mid2]，说明 midA 这条线划分出来左边的数大了，切分线应该左移。经过多次调整以后，切分线总能找到满足条件的解。
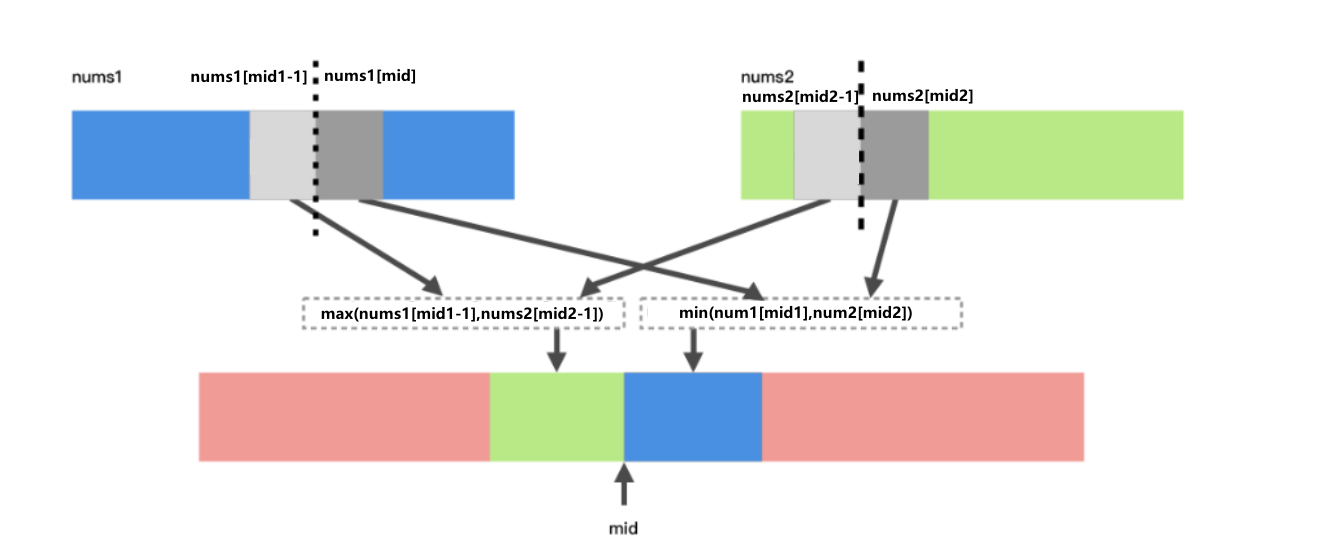
  -假设如果找到了切分的两条线了，nums1 在切分线两边的下标分别是 mid1 - 1 和 mid1。nums2 在切分线两边的下标分别是 mid2 - 1 和 mid2。怎么通过切线找到中位数呢？我们首先参考 两个数组最终合并成一个数组怎么来找的？如果数组长度是奇数，那么中位数就是 max(nums1[midA-1], nums2[midB-1])。如果数组长度是偶数，那么中间位置的两个数依次是：max(nums1[midA-1], nums2[midB-1]) 和 min(nums1[midA], nums2[midB])，那么中位数就是 (max(nums1[midA-1], nums2[midB-1]) + min(nums1[midA], nums2[midB])) / 2
  

func findMedianOfTwoSortedArrays(nums1 []int, nums2 []int) float64 {
	if len(nums1) > len(nums2) { // 这里是判断两个数组长度，把小的那个数组 作为nums1  ，把大的那个数组 作为nums2
		return findMedianOfTwoSortedArrays(nums2, nums1) // 这里用return 调用本身函数 重新 给形参赋值，把小的那个数组 作为nums1  ，把大的那个数组 作为nums2
	}
	low, high, N, mid1, mid2 := 0, len(nums1), (len(nums1)+len(nums2)+1)>>1, 0, 0 // 这里注意len(nums1)+len(nums2)+1别忘了加1，为啥要加1在除2？因为这样就能保证N在整个合并数组切线左侧一定是整个数组的一半
	for low <= high {                                                             // 判断 切分nums1数组时
		mid1 = low + (high-low)>>1 // nums1的分界线左侧是 mid-1 右侧就是mid1
		// 下面这里会有人有疑问？问什么是N-mid1作为mid2？这里解释一下，因为两个数组最终合并为一个数组的时它的一半（也就是中位数所在位置是一定的）
		// 这里分开两个数组，用各自切分线表示 就必须满足 两个切分线位置之和 == 合并一个数组一半，这样就能确保合并一个数组的中位线 一定在 两个切分线（包含两个切分线）之间
		mid2 = N - mid1                              // nums2的分界线 左侧是 mid2-1 右侧是mid2
		if mid1 > 0 && nums1[mid1-1] > nums2[mid2] { // nums1 的分界线划多了，要向左边移动一位
			high = mid1 - 1
		} else if mid1 < len(nums1) && nums1[mid1] < nums2[mid2-1] { // nums1 的分界线划少了，要向右边移动一位
			low = mid1 + 1
		} else { // 没找到合适的划分，需要输出最终结果。分为奇数和偶数2种情况
			break
		}
	}
	leftMid, rightMid := 0, 0
	if mid1 == 0 { // 走到这里说明上面没有找到合适划分
		leftMid = nums2[mid2-1]
	} else if mid2 == 0 {
		leftMid = nums1[mid1-1]
	} else {
		if nums1[mid1-1] >= nums2[mid2-1] {
			leftMid = nums1[mid1-1]
		} else {
			leftMid = nums2[mid2-1]
		}
	}
	if (len(nums1)+len(nums2))&1 == 1 { // 如果为奇数的话，那么leftMid正好是中位数
		return float64(leftMid)
	}
	if mid1 == len(nums1) { // 如果执行到这里的话就说明，就说为偶数，这样的就还需要获取rightMid，这里就是获取rigthMid
		rightMid = nums2[mid2]
	} else if mid2 == len(nums2) {
		rightMid = nums1[mid1]
	} else {
		if nums1[mid1] >= nums2[mid2] { // 因为是右切线所以 就是谁最小谁是最靠近 leftMid切线的
			rightMid = nums1[mid1]
		} else {
			rightMid = nums2[mid2]
		}
	}
	return float64(leftMid+rightMid) / 2.0
}