全连接神经网络

全连接神经网络

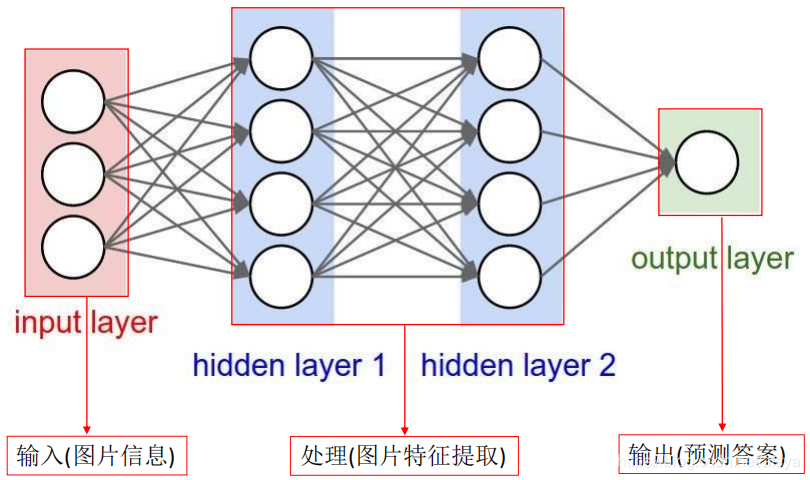
整体架构

线性函数

从输入到输出的映射

举一个例子

我们通过一个简单的全连接层来判断西瓜甜不甜，其中影响西瓜甜不甜的因素暂定为3个，分别是瓜蒂（x1）,拍西瓜产生的声音（x2）, 西瓜皮的纹路（x3）。我们将者三个作为全连接层的输入，中间隐藏层神经元的数量为4，而全连接层的输出为预测西瓜甜的概率p1和预测西瓜不甜的概率p2。

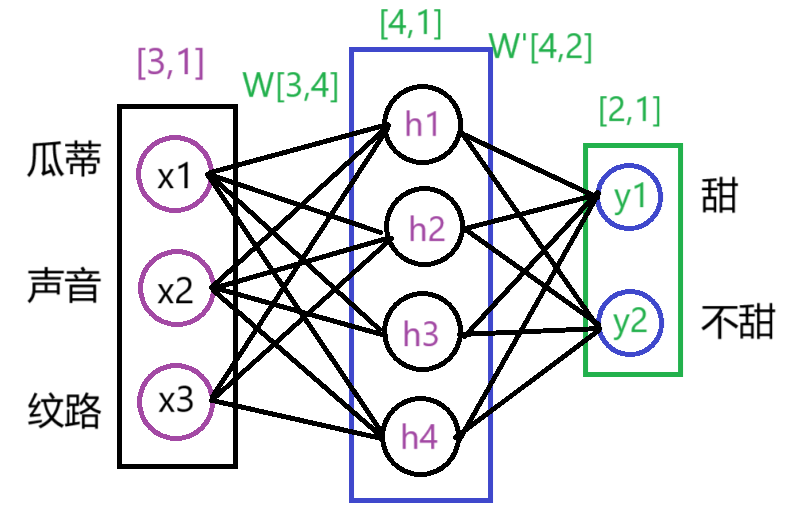
其中，我们以W[3,4]为例，进行详细说明

• W是被随机初始化的，并且初始化的值相对较小；

• W矩阵间的数值初始是没有任何关联的，经过训练一步步去试探x1,x2,x3之间的占比；

• 下面是训练一段时间后，假设W矩阵的值

  

• 关于第三条图的说明：

  • W1认为影响西瓜甜不甜的因素中，拍西瓜产生的声音（x2）对其产生的影响最大，其次是西瓜皮的纹路（x3），最后是瓜蒂（x1）；
  • W2认为影响西瓜甜不甜的因素中，西瓜皮的纹路（x3）对其产生的影响最大，其次是瓜蒂（x1），最后是拍西瓜产生的声音（x2）；
  • W3认为影响西瓜甜不甜的因素中，瓜蒂（x1）对其产生的影响最大，其次是拍西瓜产生的声音（x2），最后是西瓜皮的纹路（x3）；
  • W3认为影响西瓜甜不甜的因素中，瓜蒂（x1）和拍西瓜产生的声音（x2）对其产生的影响同等重要，最后是西瓜皮的纹路（x3）；

最后我们说一下计算过程，假设[x1,x2,x3] = [56,231,24] ,计算[h1,h2,h3,h4]

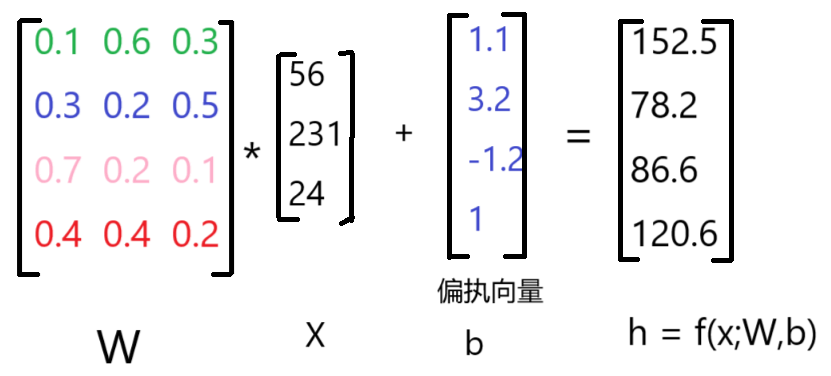
损失函数

损失函数其实有很多种，我们来看一个简单的损失函数$L_i = \sum_{i\neq y}max(0,s_j+s_{y_i}+1)$:

如何损失函数的值相同，那么意味着两个模型一样吗？

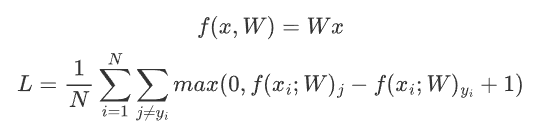
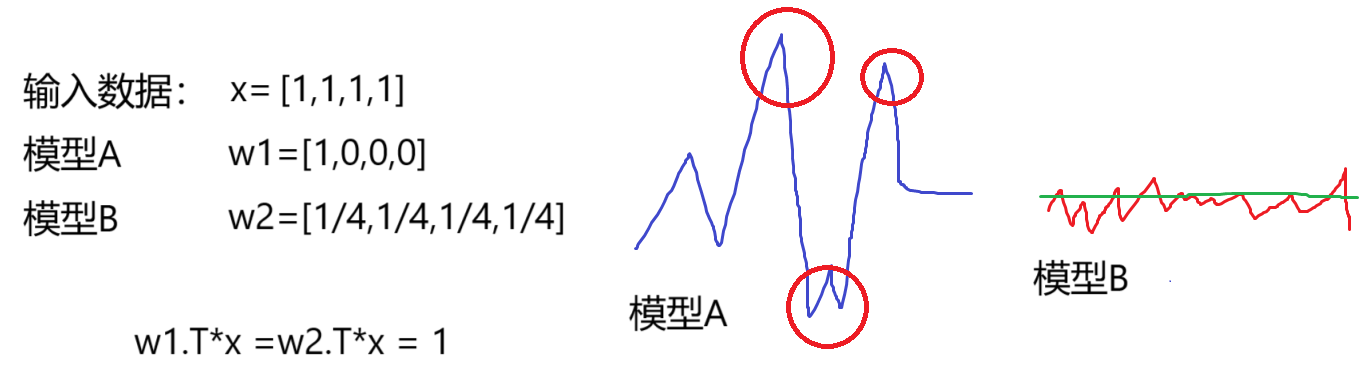
虽然损失函数的值相同,但是模型A会出现极端点，对数据的鲁棒性差；而模型B对数据的鲁棒性相对较好。

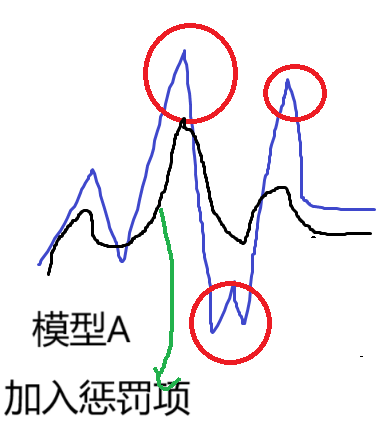
为了去掉极端点的，我们在原有的损失函数后，加入一个正则化惩罚项 ，使得极端数据点变得平滑一些

Softmax分类器

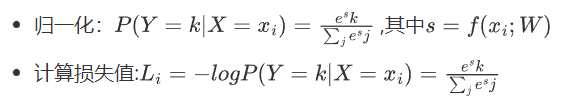
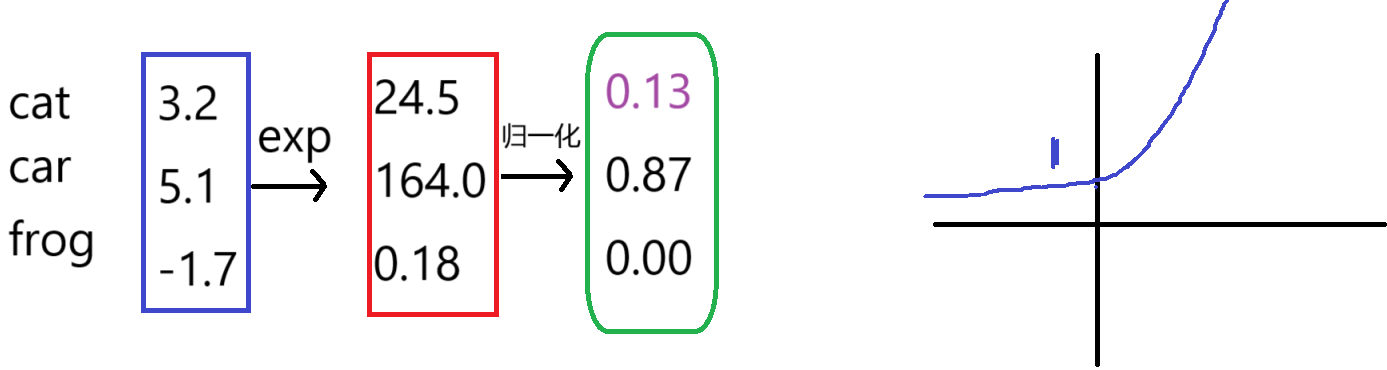
利用exp函数后，可以使得彼此之间差距。

激活函数

Sigmoid

• 数学表达式

  

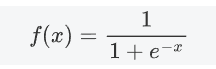
• 导数表达式

  

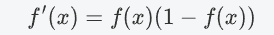
• 函数图像

  

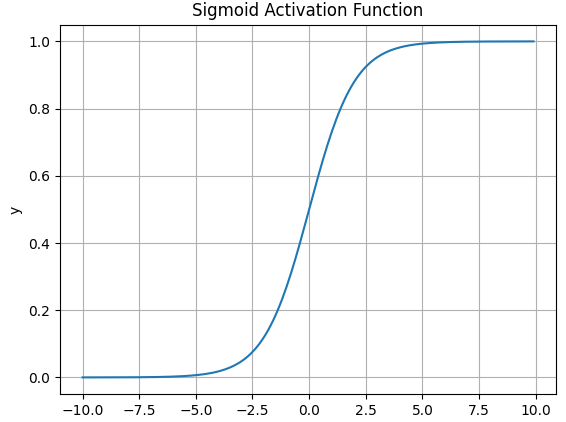
Sigmoid函数在历史上曾非常常用，输出值范围为[0,1]之间的实数。但是现在它已经不太受欢迎，实际中很少使用。

Relu

• 数学表达式

  

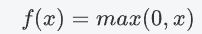
• 函数图像

  

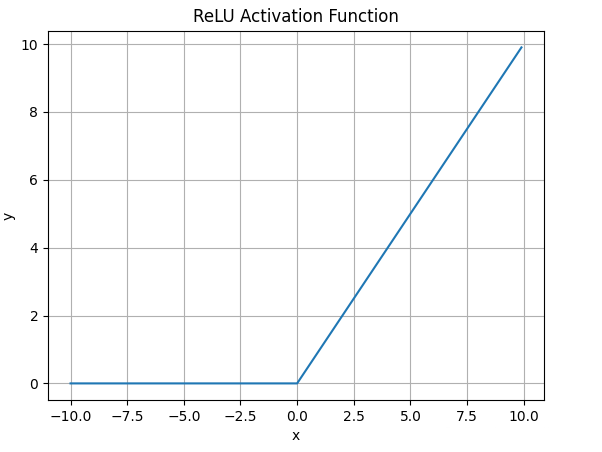
• 适用范围

  • ReLU解决了梯度消失的问题，当输入值为正时，神经元不会饱和
  • 由于ReLU线性、非饱和的性质，在SGD中能够快速收敛
  • 计算复杂度低，不需要进行指数运算

Leaky Relu函数

• 数学表达式

  

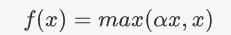
• 函数图像

  

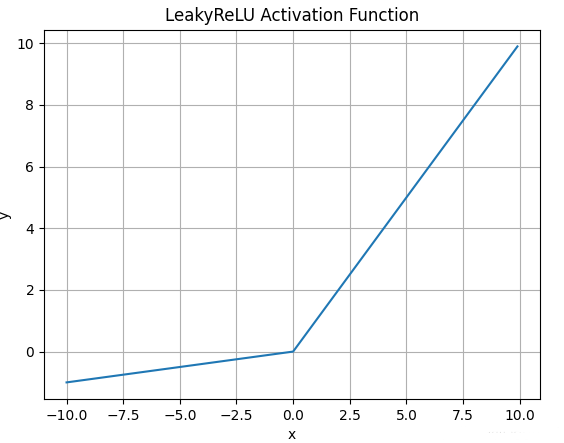
• 适用范围

  • 解决了ReLU输入值为负时神经元出现的死亡的问题

  • Leaky ReLU线性、非饱和的性质，在SGD中能够快速收敛

  • 计算复杂度低，不需要进行指数运算