QOJ板刷记录1

2025.8.12 准备开始板刷QOJ。

准备跳过所有拼尽全力找不到题解的题（怕不会做）。

本文准备记录一些做题过程中新学的知识点技巧等。

可以作为随笔看待。

---

#1. I/O Test

题意简述：

就是快读快写测试题没啥说的。

题解：

快读板子也没啥说的。

然后你需要注意的点，不要认为可以直接 cin cout 水过去，被卡了，还是得上快读。

比较坑的是如果没过不会告诉你是 WA 还是 TLE 了，会显示测试失败，遇到这种情况，大概率就是读写慢了。

---

#2. Boat

题意简述：

有 \(n\) 种不同的船，第 \(i\) 种船可以不取或者取 \([a_i,b_i]\) 个，其中如果取，那么就必须取的个数比编号比它小的船取的都多（严格大于），问有多少种取的方案。

看起来显然是 \(dp\)，时间复杂度肯定是 \(O(n^3)\) 。
不会啊，状态只会带值域，跑路看题解去了。

题解：

考虑按照每个端点把整个值域离散化成若干个区间，这样值域那一维状态数就只剩 \(O(n)\) 种了。

设 \(dp[i][j]\) 表示选到第 \(i\) 种船，选的个数在第 \(j\) 个区间的方案数。

令 \(L\) 为 \(j\) 的区间长度。

我们枚举上一个选择的个数不在 \(j\) 这个区间的船 \(k\)，并计算出从 \(k\) 到 \(i\) 共 \(m\) 个船可以取到 \(j\) 这个区间则有：

\[dp[i][j]+=\sum_{p=1}^{j-1} dp[k][p]\times C_{L+m-1}^m \]

证明如下：

我们枚举的情况是前 \(k\) 个船取得个数都小于这个区间，在 \((k,i]\) 这段区间中不能取到这个区间的船不取，能取到的船不取或者单调递增取。

显然前者的方案数 \(\sum_{p=1}^{j-1} dp[k][p]\)，后者的方案数我们可以利用组合数：

假设说我们能取到这个区间的船都取到这个区间了，那么方案数显然为\(C_L^m\)

原因是一旦单调递增，那么假设这m个船取得数字已经选出，那么他们的排列顺序一定是确定的，所以这个问题等价于从 \(L\) 个数里面挑选 \(m\) 个数了。

考虑还有尽管可以取到这个区间范围内到但是选择没取的，我们构造如下序列：

\[\underbrace{\text{0 0 0 $\dots$ 0}}_{m-1 \text{个} } \text{ 1 2 3 $\dots L$} \]

我们从这个序列里面选择 \(m\) 个数，选择第 \(i\) 个 \(0\) 就代表第 \(i\) 个可以选择的船我们没有取（所以 一共有 \(m-1\) 个 \(0\)是因为最后那一次我们钦定必须要选 ），然后剩下的数字显然选出来之后顺序还是唯一确定的。

所以我们就证明了后者的方案数是 \(C_{L+m-1}^m\)。

做 \(dp\) 的时候前者需要前缀和优化，后者组合数预处理算一下就行。

\(2D1D\)，时间复杂度是 \(O(n^3)\) 。

写完了，卡常卡了 \(n\) 个小时。

列举一些要注意的点：

你发现组合数的 \(L\) 权值可能在 \(1e9\)，预处理你需要爆算，你发现 \(m\) 的最大值一定小于 \(n\) 所以可以直接暴力组合数预处理，时间复杂度是 \(O(n^3)\) ，但是实际情况下 \(QOJ\) 就给开了 \(1s\) 会被卡常，你发现可以递推即：

\[C^{m+1}_{L+m}=C^m_{L+m-1}\times\frac{L+m}{m+1} \]

然后就过了。

---

#3. Fireworks

题意简述

给你一棵树，你可以让你任意修改边权，代价是 \(|w_i-c_i\)| 其中 \(w_i\) 是原边权，\(c_i\) 是修改之后的边权，要求最小化修改代价和使得每个叶子节点到根的距离相等。

还是只会带值域的树上 \(dp\) ，算是没救了。。。

跑路，去看题解。

先学习了一下左偏树，妙妙数据结构，准备顺便讲一下。

深刻认知到了自己闵可夫斯基和学的就是一坨，已经完全不会了。

复习了一下，发现好像没咋用到。。。

sjy 教我使用 pbds 写可并堆，发现全用不到了。。。

记一下 pbds 可并堆咋用：

__gnu_pbds::priority_queue<int> q,p;//定义一个可并堆
q.push(x);//插入
q.pop();//删除
q.top();//找堆顶
q.join(p);//p合并到q里面

题解

Part1 左偏树

首先这是一道 \(\text{SlopeTrick}\) 题目，因为 \(\text{SlopeTrick}\) 题合并凸壳经常要用可并堆，当然这道题也用了，所以首先得先会可并堆，于是自学了一下把有用的操作记录一下。

左偏树属于一种可并堆，同样属于可并堆的还有配对堆，斐波那契堆等，左偏树比较常用好学，这里讲解一下左偏树。

首对于朴素堆而言，合并需要枚举所有节点然后一个一个插进去，时间复杂度高达 \(O(n\log n)\) 显然不是我们期望的，然而左偏树可以 \(O(\log n)\) 合并两个堆，这就是左偏树的优势。

首先左偏树是一个二叉堆，要满足堆的性质，并且一个点最多有两个儿子，其次正如其名字，要满足“左偏性质”。

何为左偏性质？我们定义一个节点 \(u\) 有一个权值 \(dist_u\) 代表 \(u\) 子树下，距离 \(u\) 节点最近的空节点与 \(u\) 之间的距离。左偏树要求对于任意一个节点，其左儿子的 \(dist\) 要大于等于其右儿子的\(dist\)。

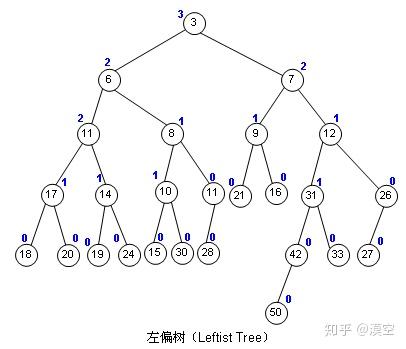
搬个图，其中点上面的数字就是它的 \(dist\)。

显然左偏树有一个性质就是 \(dist_u=dist_r+1\)。

其中 \(r\) 是 \(u\) 的右儿子，原因显然。

如图就是一个左偏树。

合并

然后左偏树的灵魂——合并操作（以小根堆为例）就是：

比较两个堆的堆顶，把较小的作为新堆顶，然后递归将其右儿子和另一个堆合并作为新的右儿子。递归过程中如果出现一个点的左儿子的 \(dist\) 小于右儿子的 \(dist\) 就将左右儿子交换。

考虑这个操作的时间复杂度，注意到一个堆的堆顶的 \(dist\) 的上界是 \(\log n\) 级别的，因为最极端的情况就是一颗满二叉树，树高显然是 \(\log n\)。如果不是满二叉树，那么一定在 \(\log\) 层以前就出现了空节点。所以证毕。

也就是说沿着左偏树一直向右儿子方向走，走的路径长度一定是 \(logn\) 的。根据递推式 \(dist_u=dist_r+1\)，根节点 \(dist\) 是 \(logn\)，也就是说一直向右儿子走最多 \(\log n\) 次就会到空节点。考虑合并的过程就是一直向右儿子方向走的过程，所以最多合并 \(logn\) 次就会达到空节点，显然如果遇到空节点我们只需要把整个堆接到空节点对应的位置就好了，所以合并的时间复杂度是 \(O(\log n)\)。

插入

插入一个点就是把这个点看成一个堆，然后做合并操作。时间复杂度 \(O(\log n)\)

删除

删除一个点比较麻烦一些，假设我们要删除一个点，需要将其左右儿子先合并，这个时间复杂度是 \(O(n\log n)\) 的，接下来将它接到要删的点祖先上面，然后更改沿途祖先的 \(dist\)，如果出现左儿子的 \(dist\) 比右儿子的小，那么交换左右儿子，一直到 \(dist\) 不改变位置。

考虑证明这一步的时间复杂度：

我们做一个分类讨论，首先是 \(dist\) 变大的情况。根据 \(dist\) 递推式，一个节点的 \(dist\) 只和右儿子的 \(dist\) 有关，所以只有所以更改沿途祖先时一定会终止于第一次成为某个节点的左儿子，而沿途全是右儿子，有根据经典结论左偏树上一个点一直沿着右儿子走走到空节点长度是 \(\log n\) 的，所以时间复杂度是 \(O(n\log n)\) 的。

其次是 \(dist\) 变小的情况，考虑到极端情况即右儿子作为新的堆顶，然而左儿子合并到右儿子上却并没有增加右儿子的 \(dist\)（考虑合并过程，\(dist\) 一定不会减小只会单调上升，最多也是不变） 这样因为删掉一个节点，所以最后新堆顶的 \(dist\) 就是右儿子的 \(dist\)，也就是说比原来少 \(1\)，这显然是减少的上界了。这样的话一直沿着祖先走到第一个左儿子，可能因为此时左儿子的 \(dist\) 等于右儿子的 \(dist\) 然而左儿子的 \(dist\) 减少后成为新的右儿子，继续改变上面的祖先节点。这种情况的终止条件是到达第一个比其祖先右儿子大的左儿子，就不会影响到祖先的 \(dist\) 了。所以这个更改的路径可以拆成两部分，一部分是从删除的点到最后一个 \(dist\) 等于右儿子的左儿子，以及从最后一个 \(dist\) 等于右儿子的左儿子到第一个 \(dist\) 大于右儿子的左儿子。显然后者的长度是 \(\log n\)，考虑前者如果左儿子的 \(dist\) 等于右儿子的 \(dist\)，那么一定有它是一颗满二叉树，否则肯定会提前出空，从而不合法，而满二叉树的树高也是 \(\log n\) 的。所以整体需要修改的路径长度是 \(\log n\) 的。那么删除的时间复杂度是 \(O(\log n)\) 的。

整体加减一个数

这个操作这需要打一个懒标记就行，在合并前 \(\text{pushdown}\) 下去就好了。没啥讲的，因为整体加减不会影响相对大小关系。

查询一个点所在的堆的堆顶

左偏树的树高不是 \(\log n\) 的，所以不要试图暴力跳来判断一个点所在的堆的堆顶是谁，你可以考虑使用并查集，每次合并都同同时使用并查集维护堆顶，如果出现把堆顶删除了的操作，那么可以把新堆顶的父亲改成自己，把删除的堆顶的父亲设置为新堆顶就好了。

---

Part2 此题正解

设 \(f_i(x)\) 代表第 \(i\) 个点子树下要使得下面的叶子到 \(i\) 的距离相等的花费代价，感性理解一下这个一定是一个下凸的分段一次函数，原因显然，叶子是一个绝对值函数，之后合并到子树的时候给凸函数相加仍然是凸函数。

考虑儿子节点合并到父亲的过程，假设 \(L\) 为 \(f_i(x)\) 取到最小值的左端点,\(R\) 为取到最小值的右端点。令\(l\) 为 \(i\) 到父亲那段路径的长度， \(g_i(x)\) 为 \(i\) 子树的叶子到父亲的距离为 \(x\) 需要的代价，那么有：

\[g_i(x) = \begin{cases} f_i(x) + l & x \leq L \\ f_i(L) + (l - (x - L)) & L < x \leq L + l \\ f_i(L) & L + l < x \leq R + l \\ f_i(L) + ((x - R) - l) & R + l < x \end{cases} \]

比较显然，随便手推推就能得出。 证明如下：

\(g_i(x)\) 显然一定需要从比 \(x\) 小的 \(f\) 转移，毕竟不能把 \(l\) 减到负数。

对于第一种情况，因为是下凸壳，从前面到这个点的斜率一定大于 \(1\) 转移一定劣，所以一定从当下转移。

对于第二种情况，也是因为下凸壳，能从 \(L\) 转移一定从 \(L\) 转移，同样的道理，再在前面的斜率一定大于 \(1\) 会更劣，选择比 \(L\) 更大的会让绝对值函数更劣。

对于第三种情况，一定可以把后面的绝对值函数变成 \(0\)，同时还取到 \(f_i\) 函数的最小值。

对于第四种情况，能从 \(R\) 转移一定从 \(R\) 转移，比 \(R\) 大的点斜率都大于 \(1\)，\(R\) 是斜率小于 \(1\) 的最靠右的点，在靠左绝对值函数就会更劣。

我们考虑使用经典 \(\text{Trick}\)，我们对于每个点 \(i\) 维护 \(f_i\) 的拐点集合，每有一个拐点就相当于下一段的一次函数相比于上一段的写斜率 \(-1\)，如果斜率相差比 \(1\) 大，就多放几个就好了。

考虑 \(f\) 和 \(g\) 函数的定义，显然有：

\[f_i(x)=\sum_{v\in son(i)}g_i(x) \]

那么如果我求出来一个点的所有儿子 \(g\) 的拐点集，那么这个点的 \(f\) 的拐点集就是儿子的拐点集的并，因为两个函数的相加后一个斜率段的变化量就是两个函数这个斜率段原来的变化量加一块，对应到拐点集就是对拐点集求并。

我们观察这个 \(g\) 函数的函数图像，可以发现一个性质，最后一个拐点开始一定是一个斜率为 \(1\) 的段。而 \(f\) 函数是由下面的儿子节点的 \(g\) 合并得到的。所以我们可以得到 \(f\) 函数最后一个拐点之后的斜率段对应的斜率就是儿子大小，这样只要有拐点集我们我们就能求出所有连续段的斜率，而我们又能求出来 \(f_{root}(0)\) （根据定义就是所有边权的和），所以只要求出来根节点的拐点集我们就能求出来最优解了。

考虑怎么求出来拐点集，对于把 \(g\) 合并到 \(f\) 的操作，我们可以直接使用可并堆，我们现在只需要考虑如何处理从 \(f\) 转化到 \(g\)。

考虑从 \(f_i\) 的函数图像到对应的 \(g_i\) 的函数图像有什么差距，其实就是给前 \(L\) 段向上平移 \(l\)，将原来的在原来的 \(L-R\) 向右平移 \(l\)，然后在平移后空缺出来的 \(L\) 到 \(L+l\) 插入一段斜率为 \(-1\) 的直线，最后把 \(R+l\) 之后的直线全删掉，改成一个斜率为 \(1\) 的直线。

对应到堆上的操作其实就是把 \(L\) 开始之后的节点全部弹掉（根据最后一个点的斜率是儿子节点数，我们只需要把前儿子节点数大小 \(+1\) 全弹掉就好了），然后插入一个 \(R+l\) 和 \(L+l\) 就好了。（考虑这个操作将 \(L-R\) 段平移了，由于 \(L\) 到 \(L+l\) 将自然接到上一个斜率为 \(-1\) 段后面，\(R+l\) 后面自然成为新的斜率为 \(1\) 的段，所以就把直接就把剩下其他操作全解决了，自然就是在 \(L\) 插入斜率为 \(-1\) 的点了）

然后就做完了。

---

#4. Gap

题意简述

交互题，交互库会生成权值在 \([0,1e18]\) 的按照升序排列的 \(N\) 个数，你每次可以查询一段区间 \([l,r]\) 得到这 \(n\) 个数中权值在查询区间的最小值和最大值，如果没有返回 \(-1\)。你需要求出最大的相邻的两个数的差。

\(\text{Subtask1}:\) 最多使用 \(\frac{N+1}{2}\) 询问。

\(\text{Subtask}2:\) 定义一次查询的代价是查询区间中包含交互库的数的个数 \(+1\)，你的查询总代价需要小于 \(3N\)。

这场 $\text{APIO} $ 唯一切出来的题，有点小唐，和 \(\text{sjy}\) 配合一块做出来了。

---

题解

Subtask1

这个子任务也太唐了，考虑到你每次查询都能得到一段区间最大值和最小值的大小，也就是可以确定出两个数的大小。那只需要第一次查询 \([0,1e18]\) 得到 \(mn\) 和 \(mx\)（所有数中最大的和最小的），下一次查询 \([mn+1,mx-1]\) 就能得到第二大的第二小的，以此类推下去，那么 \(\dfrac{n}{2}\) 次就可以得到所有的数，然后暴力扫一下就得到答案了。

Subtask2

这个子任务还算有点意思，很自然想到分块，先第一次询问 \([0,1e18]\) 得到最小值 \(mn\) 和最大值 \(mx\)，这花了 \(n+1\) 的代价，然后我们将区间 \([mn,mx]\) 匀分成 \(N\) 块，我们依次查询这些块，这花了 \(2n\) 的代价（每个数被包含一次，查询区间也有 \(n\) 次），发现多了一个代价，我们可以把左右端点扣掉（不用查也知道左右端点分别是最小的和最大的）这样就少了两次，就能在要求的查询次数之内查询出来所有块的结果。

考虑这么查询有什么用，根据鸽笼原理，显然，这 \(n\) 个数要么均匀的分布在这些块中（每个块有且只有一个数），要么存在空块，里面不存在任何数。对于前者一个块只有一个数自然没有块内贡献，对于后者由于存在空块所以空块两端最近的点的差一定大于块长，而块内贡献一定小于块长，所以也一定不存在块内贡献。不需要考虑块内贡献我们就只需要考虑块间贡献了，直接把每个块的最小值减去前面得到的最大值的差更新答案就做完了。

---

#5. 在线 O(1) 逆元

题意简述

交互题，多组查询，在线 \(O(1)\) 求一个数在模 \(998244353\) 下的逆元。

题解

参考了 \(\text{zak}\) 的做法，将他的做法搬了过来，我会阐述的更加详细一些。

大概思路就是，想要求 \(x\) 的逆元，我们考虑找到一个数 \(u\) 使得 $ux \operatorname{mod} p\le p^{\frac{2}{3}} $

这样预处理所有前 \(p^{\frac{2}{3}}\) 的 逆元，在配合 \(u\) 就可以直接得到 \(x\) 的逆元，即 \(x^{-1} \equiv (ux)^{-1}\times u\)。

考虑怎么得到 \(u\)。

我们选择使用分块，按照 \(B=p^{\frac{1}{3}}\) 分块，令 \(x=aB+c\)，其中\(a=\lfloor \dfrac{x}{B} \rfloor\)，\(c=x \operatorname{mod} B\)。那么 \(ux=uaB+uc\)。

因为 \(c<p^{\frac{1}{3}}\)，假设我们令\(u<p^{\frac{1}{3}}\)，那么\(uc\) 的数量级就对了，我们只需要让 \(uaB\) 的取值在 \([-p^{\frac{2}{3}},p^{\frac{2}{3}}]\) 就好了。

那会不会无解呢？不会的！

假设 \(uaB \equiv v \operatorname{mod} p\)。

你发现 \(u\) 的在范围内可能的取值一共有 \(2p^{\frac{1}{3}}\) 种（因为\(u \in [-p^{\frac{1}{3}},p^{\frac{1}{3}}]\)）,同样的道理 \(v\) 的取值一共有 \(2p^{\frac{1}{3}}\) 种，那么所有的点对 \((u,v)\) 一共有 \(4p\) 种，然而 \(Uab-v\) 就只有 \(p\) 种取值。根据鸽笼原理，我们一定能找到两个点对 \((u_1,v_1)\)，\((u_2,v_2)\) 使得 \(u_1ab-v_1=u_2ab-v_2\)。

那么就可以得到 \((u_1-u_2)ab\equiv v_1+v_2 \operatorname{mod}p\)。

那么\(u_1-u_2\) 就是我们要求的 \(u\)，\(v_1-v_2\) 就是我们要求的 \(v\)。所以一定有解。

考虑我们到底要怎么求。

我们考虑枚举 \(u\) （一共 \(2p^{\frac{1}{3}}\) 种取值），考虑有哪些 \(uaB\) 也在对应的取值范围内，我们将这些对应的 \(a\) 所对应的 \(u\) 更新一下。这个问题相当于我们以 \(uB\) 为步长，在圆环上走步，问第几步会落在要求的指定区间上。首先可以证明能成为答案的 \(a\) 一共只有 \(p^{\frac{1}{3}}\)（这里以及下文说的是量级） 种，考虑要求落在的要求的指定区间长度为 \(p^{\frac{2}{3}}\) ，则每圈中的 \(\frac{ p^{\frac{2}{3}}}{p}=p^{-\frac{1}{3}}\) 步会落在要求的指定区间。

所以 落在指定区间的步数 \(=\) 走的圈数 \(\times\) 每圈的步数 \(\times\) 每圈步数中落在指定区间的占比

走的圈数 \(\times\) 每圈的步数就是总步数。而总步数也就是 \(a\) 的取值范围是 \(p^{\frac{2}{3}}\) 的。

所以落在指定区间的步数一共有 \(p^{\frac{1}{3}}\) 种。

所以我们枚举 \(u\) 时只需要跳过所有不合法的 \(a\) ，因为能成为答案的 \(a\) 只有 \(p^{\frac{1}{3}}\) 种，所以时间复杂度就是 \(O(p^{\frac{1}{3}}\times p^{\frac{1}{3}})=O(p^{\frac{2}{3}})\)，至于怎么跳过，只需要找到下一个合法段到当前点的距离除以步长就知道要跳过多少步了。

还没完，我们需要预处理前 \(p^{\frac{2}{3}}\) 和后 \(p^{\frac{2}{3}}\) 个数的逆元，这一部分如果每一个都单点快速幂会多一个 \(\log\) 不优秀，我们其实可以递推做到不带 \(\log\)，后面的第 \(i\) 个数我们可以理解为 \(-i\) 的逆元，这一部分因为 \((-i)^{-1}=-i^{-1}\) 我们知道前 \(i\) 个数的逆元自然就求出来了，所以我们只需要考虑前 \(i\) 个数的逆元怎么求。

假如我们求到了第 \(i\) 个数的逆元，即 \(i\) 之前的逆元都求完了 令 \(ai+b=p\) 即 \(a=\lfloor\dfrac{p}{i}\rfloor,b=p \operatorname{mod} i\)，那么一定有 \(b<i\)。

因为模意义下 \(p \equiv0\)，所以就有：

\[ai\equiv-b \]

考虑给等式左右两边同时乘以 \(i^{-1}\) 那么有：

\[a\equiv -bi^{-1}\\ i^{-1}\equiv-ab^{-1} \]

因为 \(b\) 的逆元我们在之前已经求完了，所以我们就可以直接 \(O(1)\) 算了。