2.栈和队列
《玩转数据结构》-liuyubobobo 课程笔记
栈 Stack
- 栈是一种线性结构
- 相比数组,栈对应的操作是数组的子集
- 只能从一端添加元素(入栈),也只能从另一端取出元素(出栈),这一端被称为栈顶
- LIFP(Last In First Out)后进先出
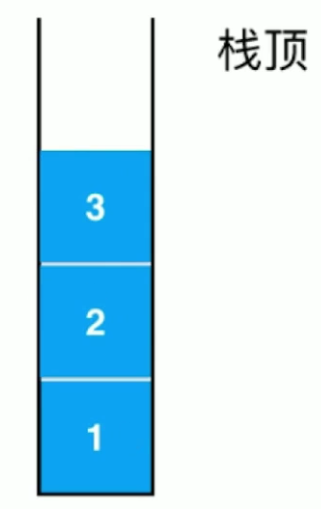
栈的应用
Undo(撤销)
输入沉迷、学习、不法,然后进行撤销
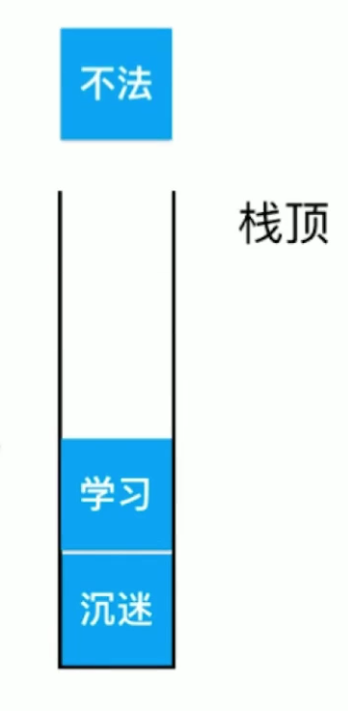
通过栈顶的元素确定最近的操作是什么,撤销就是将栈顶元素出栈
程序调用的系统栈
子过程调用
函数A调用B,函数B调用C
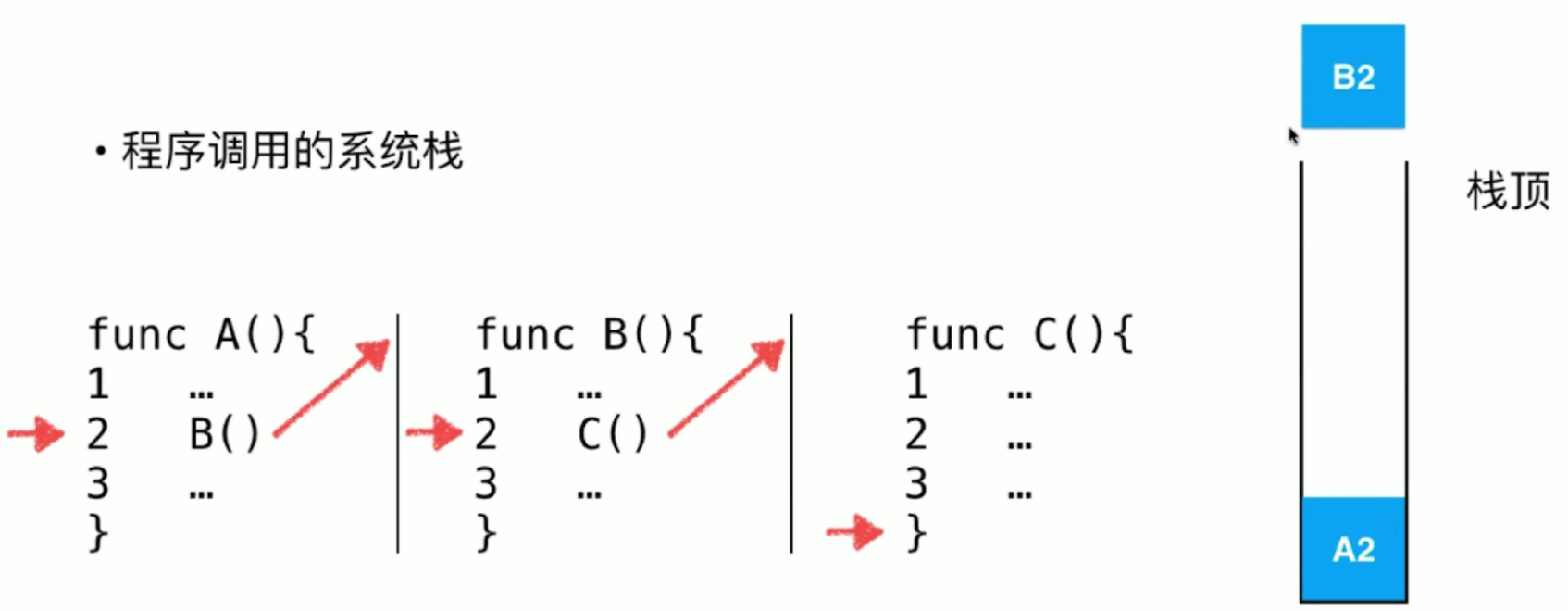
在C函数执行完成之后,通过系统栈可以知道,之前在B函数的第二行中断过,应该执行B函数的第三行
括号匹配
我们在编程的时候,经常会写很多代码块,他们之间括号套括号,这里就是括号匹配的应用,如果括号匹配失败,那么整个代码都会出错。
leetCode题目:
给定一个只包括(,),{,},[,]的字符串,判断字符串是否有效。括号必须以正确的顺序进行匹配,()和()[]{}是有效的,但是(]和([)]不是
思路:
使用栈,对字符串进行遍历,如果遇到的是左括号((,{,[)就把它压入栈,如果是一个右括号(),},])的话,就对比栈顶的元素,对比他们是否匹配,如果匹配成功,就出栈。
遍历完成之后,如果栈为空,则说明这是一个正确的括号匹配字符串
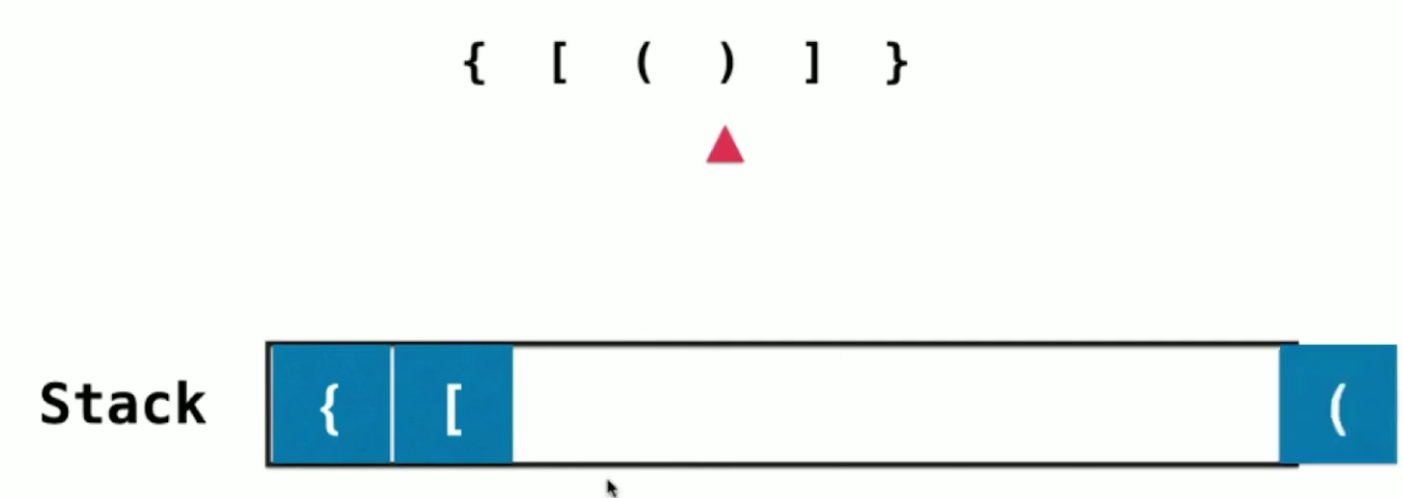
这里可以看到,栈顶元素反映了在嵌套的层次关系中,最近的需要匹配的元素
实现:
import java.util.Stack;
...
public static boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (c == '(' || c == '[' || c == '{') {
stack.push(c);
}
if (c == ')' || c == ']' || c == '}') {
char topChar = stack.pop();
if(topChar == '(' && c != ')'){
return false;
}
if(topChar == '{' && c != '}'){
return false;
}
if(topChar == '[' && c != ']'){
return false;
}
}
}
return stack.empty();
}
public static void main(String[] args) {
System.out.println(isValid("LIFP(Last In First Out)"));
System.out.println(isValid("No("));
System.out.println(isValid("No(]"));
}
>>
true
false
false
栈的实现
Stack<E>
- void push(E) 入栈
- E pop() 出栈
- E peek() 看一眼栈顶元素
- int getSize()
- boolean isEmpty()
从用户的角度来看,支持这些操作就行,具体的底层实现,用户是不关心的。实际上其底层有多种实现方式
栈接口
我们写一个栈的接口,然后具体的栈实现类实现这个接口。使用这种面向对象的思想来区分不同的实现方式
/**
* 栈接口
* @author 肖晟鹏
* @email 727901974@qq.com
* @date 2021/3/22
*/
public interface Stack<E> {
/**
* 入栈
* @param e 元素
*/
void push(E e);
/**
* 出栈
* @return 元素
*/
E pop();
/**
* 看一眼栈顶元素
* @return 栈顶元素
*/
E peek();
/**
* 获取栈中元素数量
* @return 栈中元素数量
*/
int getSize();
/**
* 判断栈是否为空
* @return true/false
*/
boolean isEmpty();
}
数组实现栈
我们使用上一章中我们自己实现的动态数组来实现栈
/**
* 使用数组在实现栈
* @author 肖晟鹏
* @email xiaocpa@digitalchina.com
* @date 2021/3/22
*/
public class ArrayStack<E> implements Stack<E> {
private MyArray<E> array;
public ArrayStack (int capacity){
array = new MyArray<>(capacity);
}
public ArrayStack(){
array = new MyArray<>();
}
/**
* 向栈顶添加一个元素
* 对应数组的最后一个元素
* @param e 元素
*/
@Override
public void push(E e) {
array.addLast(e);
}
/**
* 出栈,移除栈顶元素
* 对应数组移除最后一个元素
* @return
*/
@Override
public E pop() {
return array.removeLast();
}
/**
* 获取栈顶元素
* 对应数组获取最后一个元素
* @return
*/
@Override
public E peek() {
return array.get(array.getSize() -1 );
}
@Override
public int getSize() {
return array.getSize();
}
@Override
public boolean isEmpty() {
return array.isEmpty();
}
/**
* 获取栈容量
* @return 栈容量
*/
public int getCapacity(){
return array.getCapacity();
}
@Override
public String toString() {
StringBuilder res=new StringBuilder();
res.append("Stack:");
res.append("[");
for(int i=0;i<array.getSize();i++){
res.append(array.get(i));
if(i != array.getSize()-1){
res.append(",");
}
}
res.append("] top");
return res.toString();
}
}
使用验证:
public static void main(String[] args) {
ArrayStack<Integer> stack = new ArrayStack<>();
for(int i = 0; i < 5 ; i ++){
stack.push(i);
System.out.println(stack);
}
stack.pop();
System.out.println(stack);
}
>>
Stack:[0] top
Stack:[0,1] top
Stack:[0,1,2] top
Stack:[0,1,2,3] top
Stack:[0,1,2,3,4] top
Stack:[0,1,2,3] top
队列 Queue
- 队列也是一种线性结构
- 相比数组,队列对应的操作是数组的子集
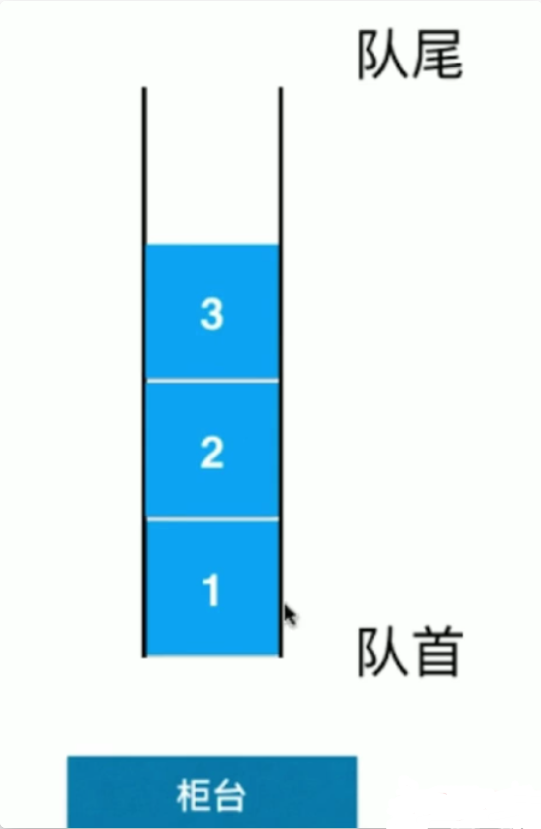
- 只能从一端(队尾)添加元素,只能从另一端(队首)取出元素
- 队列是一种先进先出(First In First Out FIFO)的数据结构
队列的实现
Queue<E>
- void enqueue(E) 入队列
- E dequeue() 出队列
- E getFront() 获取队首的元素
- int getSize()
- boolean isEmpty()
从用户的角度来看,支持这些操作就行,具体的底层实现,用户是不关心的。实际上其底层有多种实现方式
队列接口
我们写一个队列的接口,然后具体的队列实现类实现这个接口。使用这种面向对象的思想来区分不同的实现方式
/**
* 队列接口
* @author 肖晟鹏
* @email 727901974@qq.com
* @date 2021/3/23
*/
public interface Queue<E> {
/**
* 入队列
* @param e 元素
*/
void enqueue(E e);
/**
* 出队列
* @return 元素
*/
E dequeue();
/**
* 获取队首元素
* @return 队首元素
*/
E getFront();
/**
* 获取队列中元素数量
* @return 队列中元素数量
*/
int getSize();
/**
* 判断队列是否为空
* @return true/false
*/
boolean isEmpty();
}
数组实现队列
我们使用上一章中我们自己实现的动态数组来实现
import com.cupricnitrate.datastructure.MyArray;
/**
* 动态数组实现队列
* @author 肖晟鹏
* @email xiaocpa@digitalchina.com
* @date 2021/3/23
*/
public class ArrayQueue<E> implements Queue<E>{
private MyArray<E> array;
public ArrayQueue (int capacity){
array = new MyArray<>(capacity);
}
public ArrayQueue(){
array = new MyArray<>();
}
/**
* 向队尾添加一个元素
* @param e 元素
*/
@Override
public void enqueue(E e) {
array.addLast(e);
}
/**
* 队首元素出队列
* @return 队首元素
*/
@Override
public E dequeue() {
return array.removeFirst();
}
/**
* 获取队首元素
* @return 队首元素
*/
@Override
public E getFront() {
return array.get(array.getSize() - 1);
}
@Override
public int getSize() {
return array.getSize();
}
@Override
public boolean isEmpty() {
return array.isEmpty();
}
@Override
public String toString() {
StringBuilder res=new StringBuilder();
res.append("Queue:");
res.append("front [");
for(int i=0;i<array.getSize();i++){
res.append(array.get(i));
if(i != array.getSize()-1){
res.append(",");
}
}
res.append("] tail");
return res.toString();
}
}
使用:
public static void main(String[] args) {
ArrayQueue<Integer> queue = new ArrayQueue<>();
for(int i = 0 ; i < 5 ;i ++){
queue.enqueue(i);
System.out.println(queue);
}
queue.dequeue();
System.out.println(queue);
}
>>
Queue:front [0] tail
Queue:front [0,1] tail
Queue:front [0,1,2] tail
Queue:front [0,1,2,3] tail
Queue:front [0,1,2,3,4] tail
Queue:front [1,2,3,4] tail
数组队列复杂度分析
ArrayQueue<E>
- void enqueue(E) 入队列 O(1)均摊
- E dequeue() 出队列 O(n)
- E getFront() 获取队首的元素 O(1)
- int getSize() O(1)
- boolean isEmpty() O(1)
均摊是因为可能发生扩容操作
数组队列的出队时间复杂度为O(n),每次出队时,其内数组都需要向前移动元素,如果有一百万次出队,那么要的时间就很多了。
那么我们有入队出队都是O(1)时间复杂度的队列实现方法那?
答案是有的:循环队列
循环队列实现
循环队列的设计思想
数组队列的出队时间复杂度为O(n)是因为每次出队时,其内数组都需要向前移动元素。如果想要达到O(1),那么可以直接标识队首元素,每次出队的时候,维护标识即可,不去移动数组内的元素。
底层还是使用数组来实现,但是使用两个标识符:front和tail,它们别指向队首和下一次新元素入队应该存储的位置,每次出队的时候,不再移动元素,而是维护front标识,使其++,这样时间复杂度就为O(1)了
比如有一个队列,其内有a,b,c,d,e五个元素,front标识指向元素a,即索引为0的位置,tail标识指向下一次新元素入队应该存储的位置,即索引为5的位置。这个时候,元素a出队列,那么只需要将标识front ++,指向元素b,即索引为1的位置即可。
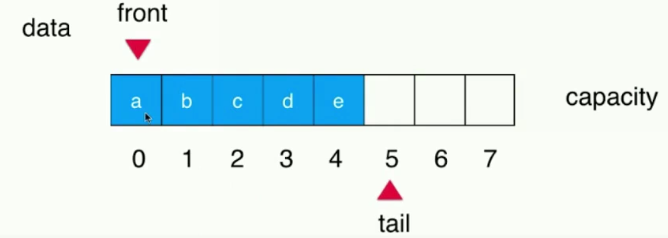
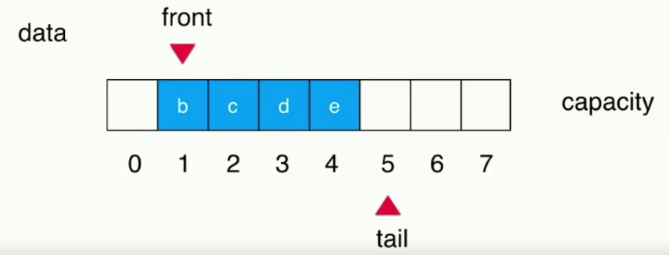
ps:capacity为数组长度,这里capacity = 8
当队列为空的时候,front == tail
入队也是同理,维护tail,使其向后移动即可
现在就有小朋友冒问号了:为什么叫做循环队列呢?
因为循坏队列是把数组看做是一个环,当tail == (capacity-1)的时候,但是front != 0 ,也就是说数组前面的还有可以利用的空间,那么tail的下一个索引,其实是0,而不是直接扩容或者报错数组空间已满
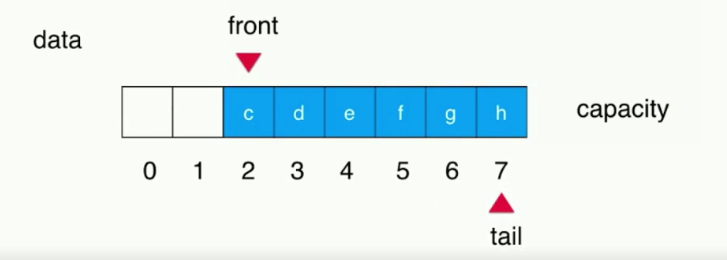
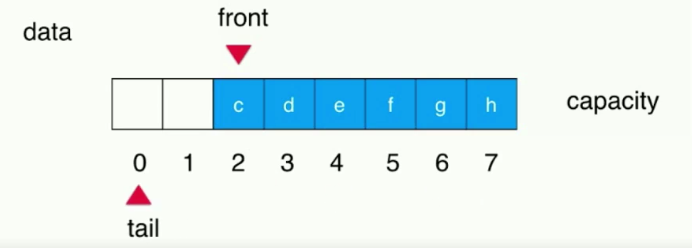
所以front和tail的移动,不应该是直接++,而是front/tail=(front/tail+1)%capacity(数组长度)
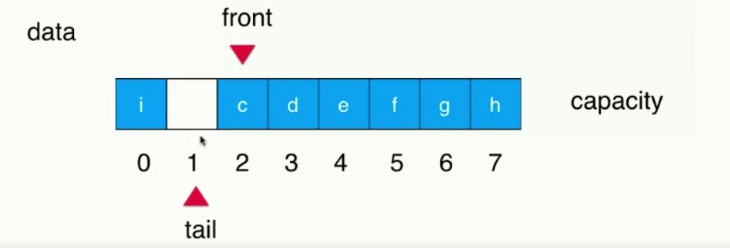
这里注意了,之前说当队列为空的时候,front == tail,那么当出现以上情况的时候,就不应该再插入元素了,因为再插入元素,就是front == tail并且队列不为空。
那么这种情况下就是队列满的情况,即(tail + 1)%capacity == front
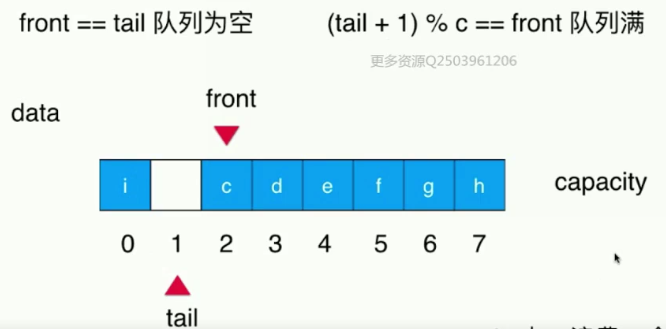
缺点:会浪费底层数组中的一个空间。
但是比起优点来说,这点缺失是我们可以接受的。
代码实现
/**
* 循环队列实现
* @author 肖晟鹏
* @email xiaocpa@digitalchina.com
* @date 2021/3/24
*/
public class LoopQueue<E> implements Queue<E> {
/**
* 缩容比例
*/
private final int RESIZE_SHRINK = 2;
/**
* 判断缩容的条件
*/
private final int RESIZE_IS_SHRINK = 4;
/**
* 扩容比例
*/
private final int RESIZE_EXPANSION = 2;
/**
* 不再使用自己实现的动态数组,而是使用静态数组
*/
private E[] data;
/**
* 队首标识
*/
private int front;
/**
* 队尾标识
*/
private int tail;
/**
* 队列中元素的个数
*/
private int size;
/**
* 队列的长度(队列能装下多少个元素)
*/
private int capacity;
public LoopQueue(int capacity){
//注意,因为需要空一个数组的空间,所以这里需要+1
this.data = (E[])new Object[capacity + 1];
this.front = 0;
this.tail = 0;
this.size = 0;
this.capacity = capacity;
}
public LoopQueue(){
this(10);
}
/**
* 获取队列长度
* @return
*/
public int getCapacity() {
return capacity;
}
/**
* 入队
* @param e 元素
*/
@Override
public void enqueue(E e) {
//判断队列是否为满,如果为满,则需要扩容
if((tail + 1) % capacity == front) {
resize( this.capacity * this.RESIZE_EXPANSION);
}
this.data[tail] = e;
tail = (tail + 1) % this.capacity;
this.size ++;
}
/**
* 出队
* @return
*/
@Override
public E dequeue() {
if(isEmpty()){
throw new IllegalArgumentException("cannot dequeue from an empty queue");
}
E ret = this.data[this.front];
this.data[this.front] = null;
this.front = (this.front + 1) % this.capacity;
this.size -- ;
//缩容
if(this.size == (this.capacity / this.RESIZE_IS_SHRINK) && this.capacity / this.RESIZE_SHRINK != 0 ){
resize(this.capacity / this.RESIZE_SHRINK);
}
return ret;
}
/**
* 获取队首元素
* @return 队首元素
*/
@Override
public E getFront() {
if(isEmpty()){
throw new IllegalArgumentException("Queue is empty");
}
return this.data[this.front];
}
/**
* 获取队列中的元素个数
* @return 队列中的元素个数
*/
@Override
public int getSize() {
return this.size;
}
/**
* 队列扩容
* @param newCapacity 新的队列长度
*/
private void resize(int newCapacity){
E[] newData = (E[])new Object[newCapacity +1];
for(int i = 0; i < this.size; i++ ){
//队列中的元素在数组中有front的偏移
newData[i] = data[(i + this.front) % this.capacity];
}
this.data = newData;
this.front = 0;
this.tail = size;
this.capacity = newCapacity;
}
@Override
public String toString() {
StringBuilder res=new StringBuilder();
res.append("Queue: size = " + this.size + " , capacity = " + this.capacity + " ");
res.append("front [");
//这种遍历方式和resize()方法中的遍历方式是相同的,可以进行互换
for(int i = this.front ; i != this.tail ;i = (i + 1) % capacity){
res.append(data[i]);
if((i + 1) % capacity != tail){
res.append(",");
}
}
res.append("] tail");
return res.toString();
}
/**
* 判断是否为空
* @return true or false
*/
@Override
public boolean isEmpty() {
return this.front == this.tail;
}
}
使用:
public static void main(String[] args) {
LoopQueue<Integer> queue = new LoopQueue<>();
for(int i = 0 ; i < 11 ;i ++){
queue.enqueue(i);
System.out.println(queue);
}
for(int i = 0 ; i < 8 ;i ++){
queue.dequeue();
System.out.println(queue);
}
System.out.println(queue);
}
>>
Queue: size = 1 , capacity = 10 front [0] tail
Queue: size = 2 , capacity = 10 front [0,1] tail
Queue: size = 3 , capacity = 10 front [0,1,2] tail
Queue: size = 4 , capacity = 10 front [0,1,2,3] tail
Queue: size = 5 , capacity = 10 front [0,1,2,3,4] tail
Queue: size = 6 , capacity = 10 front [0,1,2,3,4,5] tail
Queue: size = 7 , capacity = 10 front [0,1,2,3,4,5,6] tail
Queue: size = 8 , capacity = 10 front [0,1,2,3,4,5,6,7] tail
Queue: size = 9 , capacity = 10 front [0,1,2,3,4,5,6,7,8] tail
Queue: size = 10 , capacity = 20 front [0,1,2,3,4,5,6,7,8,9] tail
Queue: size = 11 , capacity = 20 front [0,1,2,3,4,5,6,7,8,9,10] tail
Queue: size = 10 , capacity = 20 front [1,2,3,4,5,6,7,8,9,10] tail
Queue: size = 9 , capacity = 20 front [2,3,4,5,6,7,8,9,10] tail
Queue: size = 8 , capacity = 20 front [3,4,5,6,7,8,9,10] tail
Queue: size = 7 , capacity = 20 front [4,5,6,7,8,9,10] tail
Queue: size = 6 , capacity = 20 front [5,6,7,8,9,10] tail
Queue: size = 5 , capacity = 10 front [6,7,8,9,10] tail
Queue: size = 4 , capacity = 10 front [7,8,9,10] tail
Queue: size = 3 , capacity = 10 front [8,9,10] tail
Queue: size = 3 , capacity = 10 front [8,9,10] tail
循环队列复杂度分析
LoopQueue<E>
- void enqueue(E) 入队列 O(1)均摊
- E dequeue() 出队列 O(1)均摊
- E getFront() 获取队首的元素 O(1)
- int getSize() O(1)
- boolean isEmpty() O(1)
均摊是因为可能发生扩容或缩容操作
循环队列和数组队列的比较
/**
* 数组队列和循环队列比较
* @author 肖晟鹏
* @email 727901974@qq.com
* @date 2021/3/25
*/
public class Main {
/**
* 测试运行入队和出队操作所需要的时间
* @param q 队列
* @param opCount 操作数
* @return 入队和出队的时间,单位ms
*/
private static long testQueue(Queue<Integer> q,int opCount){
long startTime = System.currentTimeMillis();
for(int i = 0; i < opCount; i++ ){
q.enqueue(i);
}
for(int i = 0; i < opCount; i++ ){
q.dequeue();
}
long endTime = System.currentTimeMillis();
return endTime - startTime;
}
public static void main(String[] args) {
int opCount = 100000;
ArrayQueue<Integer> arrayQueue = new ArrayQueue<>();
LoopQueue<Integer> loopQueue = new LoopQueue<>();
//O(n)
System.out.println("LoopQueue:" + testQueue(loopQueue,opCount) + "ms");
//O(n^2)
System.out.println("ArrayQueue:" + testQueue(arrayQueue,opCount) + "ms");
}
}
>>
LoopQueue:22ms
ArrayQueue:5258ms
可以看到,循环队列比起数组队列来说,运行效率高得多,主要体现在出队操作当中
这就是为什么我们需要对其进行数据结构的优化


 浙公网安备 33010602011771号
浙公网安备 33010602011771号