[ABC325E] Our clients, please wait a moment 分层图最短路 题解

原题链接、洛谷题面

更好的阅读体验

题意

一个国家有 \(n\) 个城市，可以看做一个无向连通图。
你有坐车和坐火车两种通行方式，对于从城市 \(i\) 到城市 \(j\)：

• 坐汽车会花费 \(D_{i,j} \times A\) 分钟
• 坐火车会花费 \(D_{i,j} \times B+C\) 分钟

给出 \(n,A,B,C\)，以及表示道路的邻接表，求从 \(1\) 号城市旅行到 \(n\) 号城市的最短路。途中可以从坐汽车转换成做火车，但不能从坐火车转换成坐汽车。

思路

很容易看出来需要无脑套最短路算法。（你能来切题一定会 Dijkstra 吧！）

至于怎么处理汽车与火车的换乘，我们需要建立一个分层图。（分层图是最短路的一大应用，你一定会吧！）

分层图共有两层：

• 第一层有节点 \(1\) 到 \(n\)。连通 \(i\) 与 \(j\) 的边权为乘坐汽车会花费的时间，即 \(D_{i,j} \times A\)。

• 第二层有节点 \(1 + n\) 到 \(n + n\)。连通 \(i + n\) 与 \(j + n\) 的边权为乘坐火车会花费的时间，即 \(D_{i,j} \times B+C\)。

• 两层之间对应的节点，如 \(i\) 与 \(i + n\) 之间，用边权为 \(0\) 的单向边连起来，表示从汽车换乘火车。其中边权为 \(0\) 是因为换乘没有代价，单向边是因为我们只能从汽车换乘到火车。

• 最终答案就是 \(1\) 号节点到 \(n + n\) 号节点的最短路。

可以配下图理解：

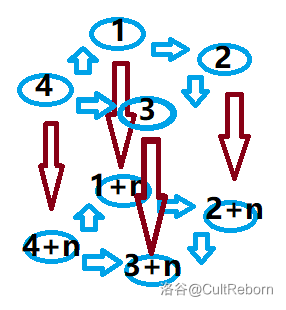
代码

AC 记录

#include<bits/stdc++.h>
#define RG register
#define IL inline
#define int long long //我很懒，但是别忘记开！
using namespace std;
const int maxn = 2003;
const int maxm = 3000006; //有分层，别开小了
IL int Read();
int n,A,B,C,head[maxm],cnt;
int dis[maxn]; bool vis[maxn];
priority_queue<pair<int,int> > q;
struct node{
	int to,nxt,cst;
}edge[maxm];
void Input(int u,int v,int w){
	edge[cnt] = {v,head[u],w};
	head[u] = cnt++; //邻接表改为链式前向星存图
}
void Dijkstra(int s){ //最短路板子，SPFA 死了
	q.push({0,s}); dis[s] = 0;
	while(!q.empty()){
		int u = q.top().second; q.pop();
		if(vis[u]) continue; vis[u] = 1;
		for(int i = head[u];~i;i = edge[i].nxt){
			int v = edge[i].to,w = edge[i].cst;
			if(dis[v] > dis[u] + w){
				dis[v] = dis[u] + w;
				q.push({-dis[v],v});
			}
		}
	}
}
signed main(){
	memset(head,-1,sizeof(head));
	memset(dis,0x3f,sizeof(dis));
	n = Read(); A = Read();
	B = Read(); C = Read();
	for(int i = 1;i <= n;++i){
		for(int j = 1;j <= n;++j){
			int x = Read();
			if(i == j) continue;
			Input(i,j,x * A); 
            //第一层汽车
			Input(i,i + n,0); 
            //两层之间换乘
			Input(i + n,j + n,x * B + C); 
            //第二层火车
		}
	}
	Dijkstra(1);
	printf("%lld",dis[n + n]);
	return 0;
}
IL int Read(){ //快读
	char c(getchar());
	int x(0),f(1);
	while(c < '0' || c > '9'){
		if(c == '-') f = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9'){
		x = x * 10 + c - '0';
		c = getchar();
	}
	return x * f;
}

2023.10.25 提交题解

2023.10.29 修改格式

求审核通过啦！