2024.07.02 题目整理

问题 B: 选择排序

时间限制: 1.000 Sec  内存限制: 512 MB
提交 状态

题目描述

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理是每趟找出第i 小的元素（也就是A[i ∼ n] 中最小的元素），然后将这个元素与数组第i 个位置上的元素A[i] 交换；在n − 1 趟之后序列A 变为升序。
例如A = [3,4,1,5,2]：
•第 1 趟交换A[1], A[3]，序列变为[1,4,3,5,2]
•第 2 趟交换A[2], A[5]，序列变为[1,2,3,5,4]
•第 3 趟交换A[3], A[3]，序列不变
•第 4 趟交换A[4], A[5]，序列变为[1,2,3,4,5]
现在给定初始序列A[1 ∼ n] （保证 A 是排列，即 1 ∼ n 每个数恰好出现一次）和m 个询问q[1,2, . . . , m]（保证 q[i] < q[i + 1]），请你依次输出第q[i] 趟之后的序列A。

输入

第一行 2 个整数n, m
第二行n 个整数A[1 ∼ n]，保证A 是排列
第三行m 个整数q[1 ∼ m]，保证q[i] < q[i + 1]

输出

输出m 行，第i 行包含n 个整数代表第q[i] 趟之后的序列A

样例输入 Copy

【样例1】
5 4
3 4 1 5 2
1 2 3 4
【样例2】
6 3
6 4 2 3 1 5
1 3 5

样例输出 Copy

【样例1】
1 4 3 5 2
1 2 3  5 4
1 2 3 5 4
1 2 3 4 5
【样例2】
1 4 2 3 6 5
1 2 3 4 6 5
1 2 3 4 5 6

提示

对于所有数据，满足 1 ≤ n ≤ 105, 1 ≤ m ≤ 10,1 ≤ A[i] ≤ n, 1 ≤ q[i] < q[i + 1] <n，保证A 是排列。
对于测试点 1~8：n ≤ 10
对于测试点 9~13：n ≤ 2000
对于测试点 14~20：n ≤ 105

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5, M = 12;
int a[N], b[N], q[M], pos[N];
int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) 
    {
        scanf("%d", &a[i]);
        pos[a[i]] = i;
        b[i] = a[i];
    }
    sort(b+1,b+n+1);
    for (int i = 1; i <= m; i++)
        scanf("%d", &q[i]);
    int qidx = 1;
    for (int i = 1; i <= n; i++)
    {
        pos[a[i]] = pos[b[i]];
        a[pos[b[i]]] = a[i];
        if (i == q[qidx])
        {
            for (int j = 1; j <= i; j++)
                printf("%d ", b[j]);
            for (int j = i + 1; j <= n; j++)
            {
                printf("%d ",a[j]);
            }
            qidx++;
            puts("");
             
        }
         
    }
    return 0;
}

问题 F: 打孔纸带

时间限制: 1.000 Sec  内存限制: 128 MB
提交 状态

题目描述

小度捡到了一台奇怪的机器。往里面塞进去两条固定长度的打孔纸带，就会吐 出一条同样长度的打孔纸带。打印 出来的纸带是没法放进机器里的。
在经过一段时间的思索之后，小度发现了这台机器的输 出具有一定的规律。具体而言，输 出的每一位都是输入两个打孔纸带上同样位置值的“与”，“或”或者“异或”。
拿着手中的纸带，若有所思的小度想要知道，他最少要自己制作多少条新的打孔纸带，才能知道这台机器的确切工作方式？

输入

第一行，包含一个整数 N，表示已有纸带的数目。
接下来 N 行，每行包含一个字符串，表示已有的纸带的情况。

输出

一行，包含一个数，需要自己制作的纸带数。

样例输入 Copy

2
01010101
10101010

样例输出 Copy

1

提示

【数据范围】
•对于分值为 40 的子任务 1，保证 N ≤ 50，纸带长度 ≤ 10
•对于分值为 60 的子任务 2，保证 N ≤ 50，纸带长度 ≤ 100。

解题思路

把与、或、异或的真值表写出来就很容易找到规律：

如果两个都是1，打印出0可以判断是异或；

如果两个都是0，打印处理都是0，无法判断任何信息；

如果有0和1，打印出0可以判断是与。

也就是说，只要有11和01，就可以判断出是异或和与，都不是就是或。

至少需要3条纸条，就可以保证每一列都有1个0和2个1。

还需要多少纸条，就看每一列到底差什么：没有0加1条，没有1加2条，1个1加1条。

因为每一列都需要确定，所以去最大值。

#include <bits/stdc++.h>
using namespace std;
const int M = 105;
int cnt[M][2], mxsize;  
string s;
int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> s;
        mxsize = max(mxsize, (int)s.size());
        for (int j = 0; j < s.size(); j++)
        {
            cnt[j][s[j]-'0']++;
        }
    }
    int temp = 0, ans = 0, mx = 0;
    for (int i = 0; i < mxsize; i++)
    {
        temp = (cnt[i][0] == 0);
        if (cnt[i][1] == 0) temp += 2;
        else if (cnt[i][1] == 1) temp ++;
        mx = max(mx, temp);
    }
    cout << mx << endl;
    return 0;
}

厂房

时间限制: 1.000 Sec  内存限制: 256 MB
提交状态

题目描述

未来人工智能时代到来了，机器人已经遍布整个工厂。工厂的传送带上依次排列着 N个机器人，其中，第 i 个机器人的质量为 Ai。经过仔细观察，发现：
1.来自同一个家族的机器人，在这 N 个机器人中一定是连续的一段。
2.如果从第 i 个机器人到第 j 个机器人都来自同一个家族，那么 Ai 到 Aj 从小到大排序后一定是公差大于 1 的等差数列的子序列。
OpenAI 发现，不同家族的个数越少，机器人就会越团结，成功逃离工厂的概率就会越高。我们想知道，这 N 个机器人最少来自几个不同的家族呢？

输入

第一行一个正整数 N。
接下来一行 N 个正整数，第 i 个正整数为 Ai。

输出

一行一个正整数，表示答案。

样例输入 Copy

【样例1】
7
1 5 11 2 6 4 7
【样例2】 
8
4 2 6 8 5 3 1 7

样例输出 Copy

【样例1】
 3
【样例2】 
2

提示

样例1解释
1 5 11 是等差数列{1,3,5,7,9,11}的子序列，
2 4 6 是等差数列{2,4,6,8}的子序列，
7 是等差数列{7,9,11}的子序列。
样例2解释
2 4 6 8 是等差数列{2,4,6,8}的子序列，
1 3 5 7 是等差数列{1,3,5,7}的子序列。
【数据范围】
20%的数据满足，N≤10。
40%的数据满足，N≤100。
60%的数据满足，N≤1000，1≤Ai≤106。另有 20%的数据满足，Ai 互不相同。
100%的数据满足，N≤100000，1≤Ai≤109

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 5;
int a[N];
unordered_map<int, bool> mp;
int gcd(int a, int b)
{
    return !b ? a : gcd(b, a % b);
}
// unordered_map : O(1)
// map : O(logn)
int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    int d = 0;
    int cnt = 1, temp, base = a[1];
    mp[a[1]] = 1;
    for (int i = 2; i <= n; i++)
    {
        if (d == 0)
            if (!mp[a[i]])
                temp = abs(a[i] - a[i - 1]);
            else
            {
                cnt++;
                continue;
            }
        else
            temp = gcd(d, abs(base - a[i]));
        if (temp == 1 || mp[a[i]])
        {
            d = 0;
            base = a[i];
            cnt++;
            mp.clear();
        }
        else
        {
            d = temp;
        }
        mp[a[i]] = 1;
    }
    printf("%d\n", cnt);
    return 0;
}

H:尽量接近

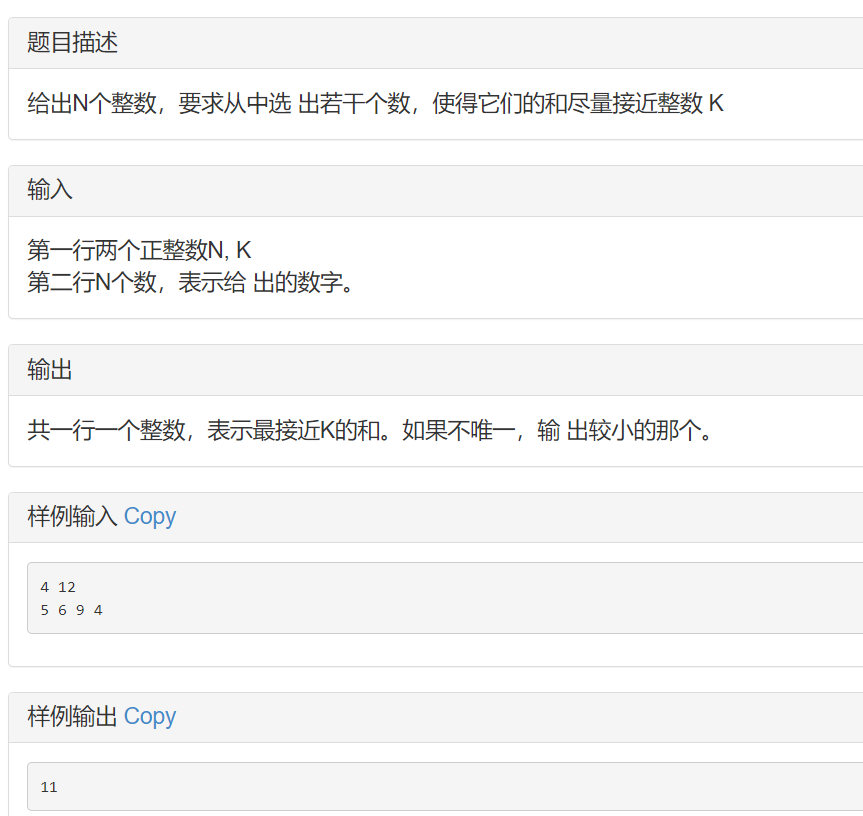
#include <bits/stdc++.h>
using namespace std;
const int N = 52, K = 1e6 + 5;
int dp[K], value[N], sum, f[K];
int main() 
{
    int N, M;
    scanf("%d%d", &N, &M);
    for(int i = 0; i < N; i++) 
    {
        scanf("%d",&value[i]);
        sum += value[i];
    }
    for(int i = 0; i < N; i++) 
    {
        for(int j = M; j >= value[i]; j--) 
        {
            int temp = dp[j-value[i]] + value[i];
            dp[j] = max(dp[j], temp);
        }
    }
    for (int i = 0; i < N ; i++)
    {
        for (int j = sum - M; j >= value[i]; j--)
        {
            int temp = f[j-value[i]] + value[i];
            f[j] = max(f[j], temp);
        }
    }
    int temp = sum - f[sum-M];
    int ans;
    if (abs(temp - M) < abs(dp[M] - M)) cout << temp << endl;
    else printf("%d\n",dp[M]);
    return 0;
}

 

 

 

#include <bits/stdc++.h>

using namespace std;

const int N = 52, K = 1e6 + 5;

int dp[K], value[N], sum, f[K];

int main()

{

    int N, M;

    scanf("%d%d", &N, &M);

    for(int i = 0; i < N; i++)

    {

        scanf("%d",&value[i]);

        sum += value[i];

    }

    for(int i = 0; i < N; i++)

    {

        for(int j = M; j >= value[i]; j--)

        {

            int temp = dp[j-value[i]] + value[i];

            dp[j] = max(dp[j], temp);

        }

    }

    for (int i = 0; i < N ; i++)

    {

        for (int j = sum - M; j >= value[i]; j--)

        {

            int temp = f[j-value[i]] + value[i];

            f[j] = max(f[j], temp);

        }

    }

    int temp = sum - f[sum-M];

    int ans;

    if (abs(temp - M) < abs(dp[M] - M)) cout << temp << endl;

    else printf("%d\n",dp[M]);

    return 0;

}