图论杂谈

最小割，Konig 定理以及 Hall 定理的结合。

本部分翻译自 CF 博客 Kőnig's and Hall's theorems through minimum cut in bipartite graphs

---

我们知道 Konig 定理，它告诉我们：二分图最小点覆盖数目等于二分图最大匹配数目。这个结论是容易记忆的。

然而，当我们想进一步了解如何构造一组确切的二分图最小点覆盖的时候，进一步的理论学习就会困难许多。

事实上，我们只需要知道两个基本的事实，就可以在任何时刻快速地构造出一组二分图最小点覆盖：

• 网络流的最大流最小割定理

• 二分图最小点覆盖数目，等于二分图最大匹配数目

我们接下来将展示如何简单地构造一组二分图最小点覆盖：

首先，利用网络流求最大匹配。如果左部点为 \(A\)，右部点为 \(B\)，对于所有 \(a\in A\)，连 \(s\rightarrow a\)，容量为 \(1\)；对于所有 \(b\in B\)，连 \(b\rightarrow t\)，容量为 \(1\)；对于所有 \((u,v)\in E,u\in A,v\in B\)，连 \(u\rightarrow v\)，边权为 \(\infty\)。最后，网络最大流就是二分图最大匹配。

然后，考虑在残量网络上，把所有 \(s\) 能到的点记作 \(S\)，其余的点记作 \(T\)。根据最大流最小割定理，割 \((S,T)\) 是最小割。

把点集 \(S\) 中，原本属于左部点的记作 \(A_S\)，原本属于右部点的记作 \(B_S\)；把点集 \(T\) 中，原本属于左部点的记作 \(A_T\)，原本属于右部点的记作 \(B_T\)。现在，让我们来看这张网络流图。

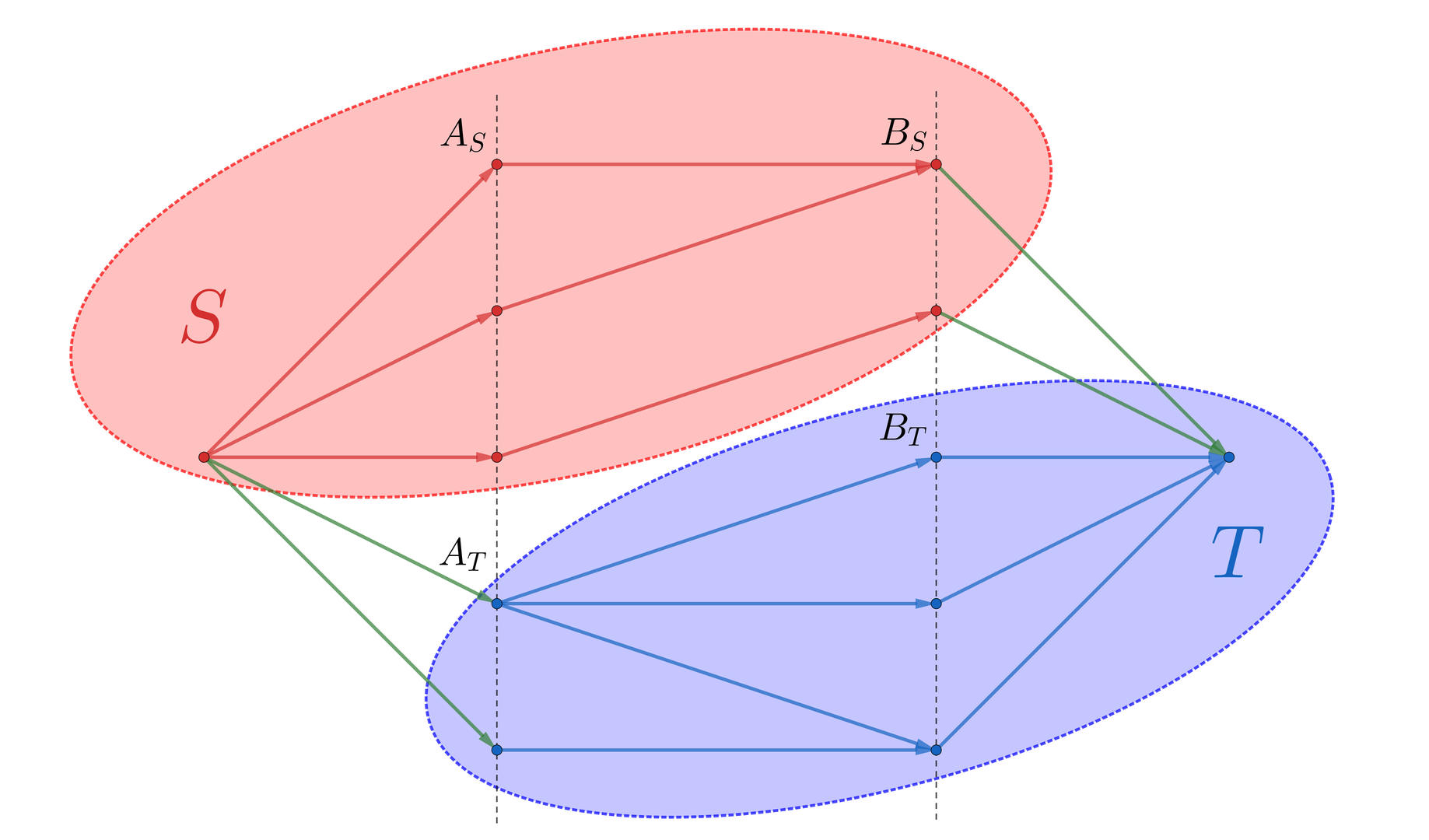
结论是，二分图的一个最小点覆盖，就是 \(A_T\cup B_S\)。

证明分为两部分：

• \(A_T\cup B_S\) 是点覆盖：二分图中不应该有 \(A_S\rightarrow B_T\) 的边，因为这样的边是割边，且容量为 \(\infty\)。而我们知道最小割的大小就是最大流，亦即最大匹配，并不是 \(\infty\)，所以这样的边不存在。换言之，二分图中的所有边 \((u,v) \mid u\in A \land v\in B\)，要么满足 \(u\in A_T\)，要么满足 \(v\in B_S\)。

• \(A_T\cup B_S\) 是最小点覆盖：因为最小点覆盖等于最大匹配。所以我们证明 \(|A_T\cup B_S|\) 是最大匹配数目即可，这等价于证明最小割大小是 \(|A_T\cup B_S|\)。而跨越 \(S，T\) 的边仅有两种可能：\(S\rightarrow a \mid a\in A_T\) 以及 \(b\rightarrow T \mid b\in B_S\)，这是我们的建图所决定了的，而这两部分的边的数目加起来就是 \(|A_T\cup B_S|\)，所以 \(A_T\cup B_S\) 确实是最小点覆盖。

这样，我们就得到了一个相当容易的，求一组最小点覆盖的算法：

通过最大流求二分图匹配。残量网络上，\(S\) 无法到达的左部点以及 \(S\) 可以到达的右部点构成一组最小点覆盖。

---

事实上利用上面的分析方法，我们还能容易地证明广义 Hall 定理。

对于二分图 \(G=(A,B,E)\)，我们称 \(G\) 是 \(k\) 匹配的，当且仅当，对于任何的 \(\alpha \subset A\)，所有和 \(\alpha\) 内的点有边相连的右部点的集合 \(\beta\) 满足：

\[k|\alpha|\le |\beta| \]

当 \(k=1\) 的时候，Hall 定理指出，\(G\) 是 \(1\) 匹配的，等价于 \(G\) 的最大匹配大小为 \(|A|\)，我们常利用 \(k=1\) 的情况，来快速判断一个图是否存在完美匹配（即还要加上 \(|A|=|B|\) 的限制，然后判断 \(G\) 是否是 \(1\) 匹配的）。

那么如果 \(G\) 是 \(k\) 匹配的，意味着什么？我们通过建图来说明：

• 对于 \(a\in A\)，连 \(s\rightarrow a\)，容量为 \(k\)。

• 对于 \(b\in B\)，连 \(b\rightarrow t\)，容量为 \(1\)。

• 对于 \((u,v) \in E,u\in A,v\in B\)，连 \(u\rightarrow v\)，容量为 \(\infty\)。

广义 Hall 定理指出，图 \(G\) 是 \(k\) 匹配的，等价于这张图的最大流大小是 \(k\times |A|\)。

如何证明两个命题等价？我们通过证明两个逆否命题来说明：

• 如果图 \(G\) 不是 \(k\) 匹配的，就意味着左部点存在一个点集 \(\alpha\)，它对应的 \(\beta\) 满足 \(k|\alpha|\gt |\beta|\)，这样的话，在最后的网络流过程中，我们显然无法把 \(\alpha\) 内的这些点的流量全部运输到 \(t\)，因为你必须经过 \(\beta\) 中的点，\(\beta\) 中的点只能最多使用一次，而你一共要运输 \(k\times |\alpha|\) 的流，超出了 \(|\beta |\) 的大小。这个逆否命题的成立，告诉我们，如果最大流大小是 \(k\times |A|\)，则图 \(G\) 一定是 \(k\) 匹配的。

• 如果图 \(G\) 的最大流大小小于 \(k\times |A|\)，也就是说最小割大小小于 \(k\times |A|\)，那么将意味着图 \(G\) 不是 \(k\) 匹配的。在这里，我们将运用上面的分析方法：容易看出最小割的大小是 \(k\times |A_T|+|B_S|\lt k\times |A|\)，移项得到 \(|B_S|\lt k\times (|A|-|A_T|)\)，也就是说 \(k\times |A_S|\gt |B_S|\)。而 \(A_S\) 中的点不可能有边与 \(B_T\) 中的点相连，所以 \(A_S\) 对应的 \(\beta\) 满足 \(|\beta|\le |B_S|\)。所以令 \(\alpha=A_S\)，我们将看到此时 \(k\times |\alpha|\gt \beta\)，所以 \(G\) 不是 \(k\) 匹配的。

这样，我们就证明了广义的 Hall 定理。

---

二分图博弈延展开去

---

二分图博弈是这样一个模型：

在一张二分图 \(G\) 上，有一个点 \(u\) 上放置了一枚棋子。先手后手轮流移动棋子，移动方式是：将棋子从当前所在顶点，移动至一个未访问过的，和当前节点有连边的顶点。不能移动的人将落败，问谁有必胜策略。

结论是，当 \(u\) 一定在最大匹配上时，先手必胜。否则先手必败。

我们分两部分来说明：

• 如果 \(u\) 一定在最大匹配上，先手随便选一个点 \(v\)，满足 \(u-v\) 出现在了一组最大匹配上即可。然后后手选的点设为 \(w\)，一定存在一个 \(x\)，满足 \(u-v,w-x\) 会同时出现在一组最大匹配；否则，我们把 \(u-v\) 换成 \(v-w\)，匹配数不会变化，与 \(u\) 一定在最大匹配矛盾，那么先手此时选这个 \(x\) 即可...... 这样下去，我们会发现，后手选完后，先手一定有对应的选，所以后手将落败。

• 如果 \(u\) 不一定在最大匹配上，那么考虑先手下一次选的点 \(v\)，\(v\) 一定在所有最大匹配上都出现过，否则你可以把 \(u-v\) 加进一组最大匹配中。所以，此时转变成了 \(1\) 的情况，先手落败。

此时，我们把问题转变了求一个点是否一定在最大匹配上。单次询问是容易的：我们求出原先的最大匹配数目，然后删去 \(u\)，就可以知道 \(u\) 是否一定在最大匹配上。

如果是所有点都询问一次呢？我们仍然可以只跑一次网络流，在 \(O(m\sqrt n)\) 的时间内解决这个问题。

---

结论：建图后跑二分图最大匹配，考虑残量网络。对于左部中的点 \(a\)，如果可以从 \(s\) 到达 \(a\)，等价于 \(a\) 不一定在最大匹配上；对于右部中的点 \(b\)，如果可以从 \(b\) 到达 \(t\)，等价于 \(b\) 不一定在最大匹配上。

证明：我们来考虑左部的情况，右部是类似的。

如果 \(s\rightarrow a\) 这条边在残量网络中依旧可达，说明你随便求了一组最大匹配，就不包含 \(a\)；否则，考虑 \(s\) 到 \(a\) 的路径，容易发现路径形如这样：\(s\rightarrow a_1\rightarrow b_1\rightarrow a_2\rightarrow b_2 \rightarrow a\)（你可以往里面多塞几组 \(a,b\)）。那么因为残量网络里 \(b_1\) 能到 \(a_2\)，说明正向的 \(a_2\rightarrow b_1\) 的边流量为 \(1\)，类似地，最后我们可以发现 \(a_2 - b_1\) 以及 \(a-b_2\) 是所求匹配里的两组边。那么我们换成 \(a_1-b_1\) 以及 \(a_2-b_2\)，这样依旧是两组边，但是匹配里不包含了 \(a\)。也就是说 \(a\) 不一定在最大匹配上；反过来，如果 \(a\) 在当前的最大匹配，但不一定在所有的最大匹配上，那么我们肯定是考虑调整，即类似匈牙利的过程，删去 \(a\)，然后为 \(a\) 的对应点 \(b_1\) 找一个新的 \(a_2\) 去匹配，重复这个过程知道找到一个空置的点。这个空置的点一定在左部，设为 \(x\)，那么其实残量网络就存在一条和上面提到的形式相同，\(s\rightarrow x\rightarrow ... \rightarrow a_2\rightarrow b_1\rightarrow a\) 的路径。所以这两个命题等价。

事实上，我们还可以判断二分图的一个点是否可能在最大匹配上，把最大匹配换成最小覆盖/最大独立集，甚至可以判断一般图的某个点是否可能/一定在最大匹配上，都是可做的。