数论学习笔记

线性筛

https://www.cnblogs.com/Creed-qwq/p/13501520.html

埃氏筛

这是进行了优化的埃氏筛，复杂度依然为\(O(nloglogn)\)
经过测试，实际运行中在n<=1e9时，其复杂度为\(O(kn),k<=3\)
就速度而言，丝毫不亚于线性筛。
这里的优化主要有两个，简单解释一下
1.\(i*i<=n\)
对于\(<=n\)的非质数，其一定存在至少一个非自身的\(<=\sqrt{n}\)的约数
因此只需枚举到\(\sqrt{n}\)即可

2.\(j=i*i\)
对于任意\(<i*i,i是质数\)的非质数而言，它的最小质因子一定小于i
根据这个原理，它一定会已经被那个更小的质因子筛掉了，因此无需重复

这里还有一个需要提到的东西就是
对于\(1\)到\(n\)枚举每一个数的质因子，这个复杂度也是\(O(nloglogn)\)
注意这里的实现必须借助线性筛提前预处理每一个数字的最小质因子和最小值因子的最大次幂
实际测试中这个\(loglogn\)远不如刚才埃氏筛的复杂度，大概在20~30左右，可以认为是一个比较小的\(log\)

顺便扔一个和这个有关的题目
https://ac.nowcoder.com/acm/contest/7501/A

bool is_prime[N];
int cnt,f[N],c[N],prime[N];
void prepare(int n)
{
	memset(is_prime,true,sizeof(is_prime));
	c[1]=f[1]=1;is_prime[1]=false;
	for(int i=1;i<=n;i++)
	{
		if(is_prime[i])prime[++cnt]=i,f[i]=c[i]=i;
		for(int j=1;j<=cnt;j++)
		{
			ll x=1ll*i*prime[j];
			if(x>n)break;
			is_prime[x]=false;
			c[x]=prime[j];
			if(i%prime[j])f[x]=prime[j];
			else {f[x]=f[i]*prime[j];break;}
		}
	}
}
int main()
{
	int n=read();
	prepare(n);
	for(int i=1;i<=n;i++)
	{
		
		int x=i;
		cout<<i<<" ";
	    while(x!=1)cout<<c[x]<<" ",x/=f[x];//这里的c[x]即为最小质因子 
		cout<<endl;
	}
	return 0;
}

调和级数枚举

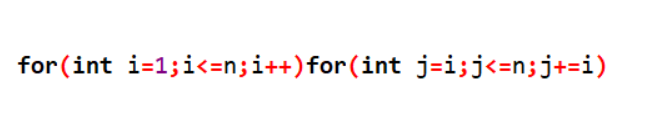
复杂度O(nlogn)
实际测试中，这个\(logn\)还蛮大的
\(1e5---->120\)
\(1e6---->170\)
\(1e7---->190\)