基础算法
[ABC241D] Sequence Query
Description
有一个空序列 \(a\)。给定 \(q\) 次操作,每次询问是以下三种之一:
1 x:向 \(a\) 中插入元素 \(x\)。2 x k:输出 \(a\) 中所有 \(\le x\) 的元素中的第 \(k\) 大值。如果不存在输出-1。3 x k:输出 \(a\) 中所有 \(\ge x\) 的元素中的第 \(k\) 小值。如果不存在输出-1。
Solution
考虑使用 set 维护。
操作 \(1\) 直接 s.push(x) 即可。
剩下两个操作我们可以分开考虑,先找到 \(a\) 中所有 \(\le x\) 的元素中最大的,然后从大往小跳 \(k\) 次即可。
相对地,对于操作 \(3\) 我们可以考虑先用 lower_bound 找到 \(a\) 中所有 \(\ge x\) 的数中最小的,然后往大跳 \(k-1\) 次即可。
注意:lower_bound 找的是 \(a\) 中所有 \(\ge x\) 的数中最大的,所以只需要跳 \(k-1\) 次
#include<bits/stdc++.h>
#define int long long
using namespace std;
multiset<long long>s;
long long T;
inline void solve(){
cin>>T;
while(T--){
int opt,x,k;
cin>>opt>>x;
if(opt==1){
s.insert(x);
}
else if(opt==2){
cin>>k;
auto it=s.upper_bound(x);
int ok=1;
while(k){
if(it==begin(s)){
ok=0;
break;
}
k--;
advance(it,-1);
}
if(ok){
cout<<*it<<endl;
}
else{
cout<<-1<<endl;
}
}
else{
cin>>k;
k--;
auto it=s.lower_bound(x);
int ok=1;
while(k){
if(it==end(s)){
ok=0;
break;
}
k--;
advance(it,1);
}
if(it==end(s)){
ok=0;
}
if(ok==1){
cout<<*it<<endl;
}
else{
cout<<-1<<endl;
}
}
}
}
signed main(){
solve();
return 0;
}
[ABC212D] Querying Multiset
Description
给你一个集合,让你支持三种操作:
-
将 \(x\) 加入集合。
-
把集合中的数都加上 \(x\)。
-
将集合中最小的数删除,并且输出这个数。
Solution
考虑使用优先队列维护这个集合。
注意到操作 2 这个区间加比较难维护,可以考虑设置一个增加量 \(s\) 来代表所有操作 2 中增加的数。
那么在操作 1 中,输入的 \(x\) 没有增加过 \(s\) ,所以直接 push(x-s)。
在操作 2 中比较简单,直接把 \(x\) 加到 \(s\) 里即可。
操作 3 ,直接输出 \(x+s\)。
然后就做完了,复杂度 \(O(T\log |S|)\)。
#include<bits/stdc++.h>
#define int long long
using namespace std;
long long T,opt,x;
long long diff=0;
priority_queue<int>pq;
signed main(){
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>T;
while(T--){
cin>>opt;
if(opt==1){
cin>>x;
pq.push(diff-x);
}
else if(opt==2){
cin>>x;
diff+=x;
}
else{
cout<<diff-pq.top()<<endl;
pq.pop();
}
}
return 0;
}
P3076 [USACO13FEB] Taxi G
Description
有一条长度为 \(m\) 的数轴,有 \(n\) 头牛需要坐车前往别的地方,起点和终点分别为 \(a_i\) 和 \(b_i\)。
现在一辆出租车从原点出发,要运送完所有牛,最后到达最右端 \(m\),求最小路程。出租车只能一次载一只牛。
Solution
我们先来看一下样例。
2 10
0 9
6 5
不难发现其中有 \(a_i>b_i\) 的情况。而且题中指出一次只能载一头牛,所以会出现以下的情形:
你把第一头牛从 0 送到 6,然后把他扔了,再把第二头牛从 6 送回到 5。
你从 5 空载走到 6 ,最后把第一头牛从 6 送到 9,再走到终点 \(m\)。
我们观察一下这个式子的构成(我们不妨认为自己是一头奶牛,要把自己从起点 0 送到终点 \(m\))。
由于每头牛至少要从自己的起点走到终点,所以答案中必然包含 \(\sum_{i=1}^{n} |a_i-b_i|\)。
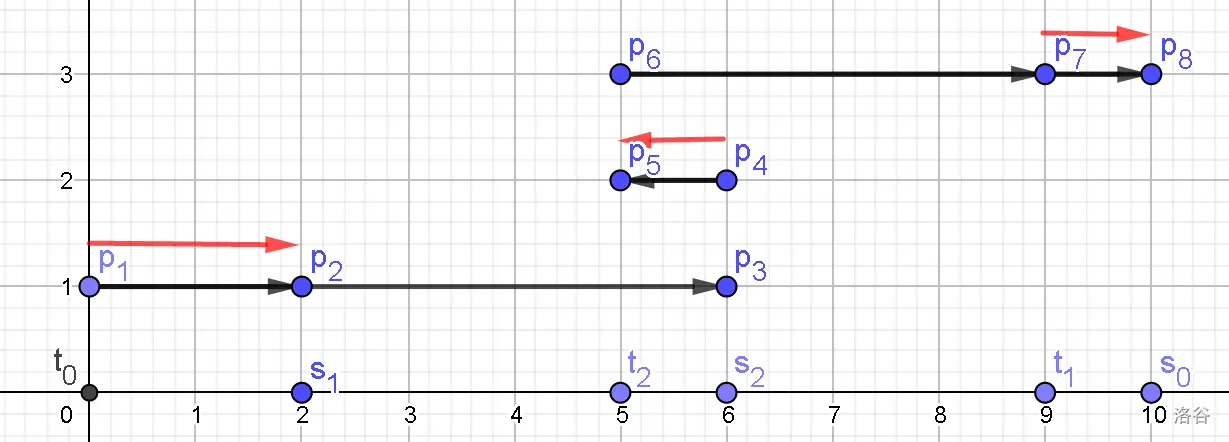
看上面这个图能帮助理解。不难发现每个红线都是从 \(a_i\) 到 \(b_j\),所以最终答案就是
现在我们的任务变成了最小化 \(\sum |a_i-b_j|\)。考虑对 \(a\) 和 \(b\) 排序即可。
#include<bits/stdc++.h>
using namespace std;
long long n,m,a[100010],b[100010],ans;
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i]>>b[i];
ans+=abs(a[i]-b[i]);
}
a[n+1]=m;
b[n+1]=0;
sort(a+1,a+n+2);
sort(b+1,b+n+2);
for(int i=1;i<=n+1;i++){
ans+=abs(a[i]-b[i]);
}
cout<<ans<<endl;
return 0;
}
最后是证明。
假设当前的方案不是最优,那么一定存在至少一对 \(i,j\),使得接第 \(j\) 头牛比接第 \(i\) 头牛更优。那我们不妨计算交换 \(i\) 和 \(j\) 所产生的影响。
经过排序后,\(a_i<a_{j}\),且 \(b_i<b_{j}\)。交换前对答案的贡献为 \(|a_i-b_i|+|a_j-b_j|\)。
交换后,贡献为 \(|a_{i}-b_j|+|b_i-a_j|\),显然不优。
P4105 [HEOI2014] 南园满地堆轻絮
Description
给你一个长度为 \(n\) 的正整数序列 \(a\),让你构造一个单调不降的正整数序列 \(b\),使得下面式子的值尽量小。
其中 \(n\le 5\times 10^6\)。
Solution
注意到经典的“最小值最大”,考虑二分。
我们从对比 \(a_i\) 和 \(b_i\) 的角度来看,\(|a_i-b_i|\) 其实就是指你构造出的 \(b_i\) 和 \(a_i\) 的偏差值,我们要让这个东西最小。
假设对于一对 \(a_i\) 和 \(b_i\),我们有一个符合条件且最小的偏差值 \(x\),那么 \(x+1\) 一定符合条件,因此有单调性,可以二分。
然后就好搞了。对于每一个 \(i\) ,我们二分 \(a_i\) 的最小偏差值。如果减去最小偏差值后得到的 \(b_i\) 不能满足条件(让 \(b\) 序列单调不降),那就让 \(b_i=b_{i-1}\),如果可行那就直接赋值。
复杂度为 \(O(n\log n)\),可以通过。
#include<bits/stdc++.h>
using namespace std;
long long n,Sa,Sb,Sc,Sd,mod,a[5000005],b[5000005];
inline long long calc(int x){
return (((Sa*x%mod*x%mod*x%mod+Sb*x%mod*x%mod)%mod+Sc*x%mod)%mod+Sd)%mod;
}
inline bool check(int x){
for(int i=1;i<=n;i++){
b[i]=a[i];
}
for(int i=1;i<=n;i++){
if(b[i]+x<b[i-1]){
return 0;
}
if(b[i]<b[i-1]){
b[i]=b[i-1];
}
else{
b[i]=max(b[i-1],b[i]-x);
}
}
return 1;
}
signed main(){
cin>>n>>Sa>>Sb>>Sc>>Sd>>a[1]>>mod;
for(int i=2;i<=n;i++){
a[i]=(calc(a[i-1])+calc(a[i-2]))%mod;
}
int l=0,r=6e9;
int minx=INT_MAX;
while(l<=r){
int mid=(l+r)/2;
if(check(mid)){
r=mid-1;
minx=min(minx,mid);
}
else{
l=mid+1;
}
}
cout<<minx<<endl;
return 0;
}
P4064 [JXOI2017] 加法
Description
给你一个长度为 \(n\) 的正整数序列 \(A\),再给你 \(m\) 个区间,让你在这 \(m\) 个区间中选出 \(k\) 个进行区间加 \(a\) 操作(\(a\) 为常数),使得 $\min{{A_i}}$ 最大化。
Solution
又是经典的最小值最大化,考虑二分这个最小值。
注意到最小值一定在 \([\min{A_i},\min{A_i}+m\times a]\) 这个范围内,直接二分即可。
如何 check 呢?
我们从前到后扫一遍 \(A_i\),如果发现有 \(A_i<\text{mid}\),就考虑用区间覆盖 \(A_i\)。对于这类用区间覆盖点的题,一个常用的 trick 是用右端点尽量靠右的区间来包含这个点。那么我们就可以先对右端点排序,再用大根堆来维护。
现在需要的是一个支持区间加单点求值的数据结构,考虑使用 Vector 😃
#include<bits/stdc++.h>
#define int long long
using namespace std;
long long T,n,m,k,s,a[200005],l,r,ans,d[200005];
vector<int>e[200005];
bool check(){
priority_queue<int> q;
int u=0,v=0,m=(l+r)/2;
memset(d,0,sizeof(d));
for(int i=1;i<=n;i++){
for(int j:e[i]){
q.push(j);
}
v+=d[i];
while(a[i]+v<m){
u++;
if(q.empty()||q.top()<i||u>k){
r=m-1;
return 0;
}
v+=s;
d[q.top()+1]-=s;
q.pop();
}
}
l=m+1;
ans=m;
return true;
}
signed main(){
cin>>T;
while(T--){
cin>>n>>m>>k>>s;
for(int i=1;i<=n;i++){
cin>>a[i];
e[i].clear();
}
for(int i=1;i<=m;i++){
cin>>l>>r;
e[l].push_back(r);
}
l=0,r=1e9;
ans=0;
while(l<=r){
check();
}
cout<<ans<<endl;
}
return 0;
}
P2048 [NOI2010] 超级钢琴
Description
给你一个长度为 \(n\) 的序列 \(A\),要求出所有长度在 \(L\) 到 \(R\) 之间的区间中区间和前 \(k\) 大的区间的区间和之和。
Solution
考虑设计一个类似 dp 状态的东西:令三元组 \((o,l,r)\) 代表区间左端点为 \(o\),右端点在 \(l,r\) 区间内的区间和最大值。
我们考虑从 \(1\) 到 \(n\) 枚举每一个 \(o\),再从 \(o+L-1\) 开始枚举。贪心地想,最终答案包含了满足条件的区间的前 \(k\) 大,那就可以用一个优先队列来存三元组,每次得到 最大值 就加到答案里,求 \(k\) 次就是最终的答案。
这个静态区间最大值就可以使用 ST 表预处理。
本题有个坑:
假设当前三元组 \((o,l,r)\) 中区间和最大的区间右端点为 \(p\),在计算完 \((o,p)\) 对答案的贡献后,\(p\) 的左边和右边仍可能产生贡献。所以在维护优先队列时应额外 push 两次。
push(o,l,p-1);
push(o,p+1,r);
复杂度为 \(O(k\log n)\),可以通过。
#include<bits/stdc++.h>
#define int long long
using namespace std;
long long n,k,L,R,A[500005],sum[500005],ST[500005][25],ans;
inline int query(int l,int r){
int k=log2(r-l+1);
int x=ST[l][k],y=ST[r-(1<<k)+1][k];
if(sum[x]>sum[y]){
return x;
}
return y;
}
struct node{
int o,l,r,t;
node(){};
friend bool operator <(const node &a,const node &b){
return sum[a.t]-sum[a.o-1]<sum[b.t]-sum[b.o-1];
}
};
inline node get_t(int o,int l,int r){
node xx;
xx.o=o;
xx.l=l;
xx.r=r;
xx.t=query(l,r);
return xx;
}
priority_queue<node>q;
inline void init(){
for(int i=1;i<=n;i++){
ST[i][0]=i;
}
for(int j=1;(1<<j)<=n;j++){
for(int i=1;i+(1<<j)-1<=n;i++){
int x=ST[i][j-1],y=ST[i+(1<<(j-1))][j-1];
if(sum[x]>sum[y]){
ST[i][j]=x;
}
else{
ST[i][j]=y;
}
}
}
return;
}
signed main(){
cin>>n>>k>>L>>R;
for(int i=1;i<=n;i++){
cin>>sum[i];
sum[i]+=sum[i-1];
}
init();
for(int i=1;i<=n;i++){
if(i+L-1<=n){
q.push(get_t(i,i+L-1,min(i+R-1,n)));
}
}
for(int i=1;i<=k;i++){
int o=q.top().o;
int l=q.top().l;
int r=q.top().r;
int t=q.top().t;
q.pop();
ans+=sum[t]-sum[o-1];
if(l!=t){
q.push(get_t(o,l,t-1));
}
if(t!=r){
q.push(get_t(o,t+1,r));
}
}
cout<<ans<<endl;
return 0;
}




 对的对的
对的对的

 浙公网安备 33010602011771号
浙公网安备 33010602011771号