C语言中递归思想的应用

C语言中递归思想的应用

一、递归思想

在C语言中，函数是程序的基本单位，每个函数负责解决特定问题。但如果程序中出现n个相同的问题，就需要调用对应函数n次，这会导致程序冗长、可读性差。那么，有没有更简洁的解决方案呢？

答案是递归函数。递归函数并非万能，它更适用于解决数学相关问题。递归函数指的是在函数内部反复调用自身的函数，其核心思想是将一个复杂的大问题拆解为多个类似的小问题，通过解决小问题并将结果逐层向上传递，最终解决大问题，整个过程包含递进和回归两个阶段。

二、递归函数的注意事项

使用递归函数时必须格外谨慎，必须提前明确终止条件。如果缺少终止条件，函数会陷入死循环，不断自我调用。由于每次函数调用都会占用一块栈空间，无限递归会导致栈溢出，引发段错误，最终使程序崩溃。

三、递归思想的实际应用案例

1. 计算n的阶乘

问题描述：用户通过键盘输入一个正整数n，设计递归函数求n！的结果。

实现代码：

/*******************************************************************
*
*	file name:	Factorial.c
*	author	 :  str41379@163.com
*	date	 :  2025/09/15
*	function :  计算n的阶乘  1*2*3*4*...*n-1*n  考查递归思想解决问题
* 	note	 :  None
*
*	CopyRight (c)  2024-2025   str41379@163.com   All Right Reseverd 
*
* *****************************************************************/



int func(unsigned int n)
{

	//递归函数必须提前写好终止条件,当n==1时可以选择终止函数
	if (1 == n)
	{
		return 1;
	}
	else
	{
		return func(n-1)*n;
	}

}



int main(int argc, char const *argv[])
{	
	
	int data = func(5); // data = 1*2*3*4*5;
	
	return 0;
}

原理说明：阶乘的递归逻辑基于n! = n * (n-1)!，当n=1时，阶乘结果为1（终止条件），通过不断将n减小并递归调用，最终回归得到结果。

2. 字符串逆序输出

问题描述：通过scanf输入字符串，在主函数中申请堆内存存储字符串，利用递归实现字符串逆序输出（如"hello"输出为"olleh"）。

实现代码：

/*******************************************************************
*
*	file name:	reversePrint.c
*	author	 :  str41379@163.com
*	date	 :  2025/09/15
*	function :  实现一个字符串的逆序输出       考查递归思想解决问题
* 	note	 :  None
*
*	CopyRight (c)  2024-2025   str41379@163.com   All Right Reseverd 
*
* *****************************************************************/


#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

// 递归函数实现字符串逆序输出
bool reversePrint(char *ptr)
{
    // 终止条件：遇到字符串结束符'\0'
    if ('\0' == *ptr)
    {
        return false;
    }
    
    // 递进：先处理下一个字符
    reversePrint(ptr + 1);
    
    // 回归：输出当前字符（逆序关键）
    printf("%c", *ptr);
}

int main(int argc, char const *argv[])
{
    // 申请堆内存并初始化（初始化为'\0'）
    char *str = (char *)calloc(1, 100);
    if (NULL == str)
    {
        perror("堆内存申请失败！");
        return -1;
    }
    
    // 输入字符串
    printf("请输入一个字符串: ");
    scanf("%s", str);
    
    // 调用递归函数逆序输出
    printf("逆序输出: ");
    reversePrint(str);
    printf("\n");
    
    // 释放堆内存
    free(str);
    str = NULL;
    
    return 0;
}

原理说明：递归先递进至字符串末尾（遇到'\0'），然后在回归过程中依次输出字符，从而实现逆序效果。

3. 计算字符串实际长度

问题描述：申请堆内存，通过scanf输入字符串并存储，利用递归计算字符串实际长度（可与库函数strlen对比结果）。

实现代码：

/*******************************************************************
*
*	file name:	strLength.c
*	author	 :  str41379@163.com
*	date	 :  2025/09/15
*	function :  计算一个字符串的实际长度       考查递归思想解决问题
* 	note	 :  None
*
*	CopyRight (c)  2024-2025   str41379@163.com   All Right Reseverd 
*
* *****************************************************************/


#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// 递归函数计算字符串长度
int strLength(char *ptr)
{
    // 终止条件：遇到'\0'，长度为0
    if ('\0' == *ptr)
    {
        return 0;
    }
    else
    {
        // 递进：当前字符长度+后续字符串长度
        return strLength(ptr + 1) + 1;
    }
}

int main(int argc, char const *argv[])
{
    // 申请堆内存并初始化
    char *str = (char *)calloc(1, 100);
    if (NULL == str)
    {
        perror("堆内存申请失败！");
        return -1;
    }
    
    // 输入字符串
    printf("请输入一个字符串: ");
    scanf("%s", str);
    
    // 调用递归函数计算长度并输出
    printf("字符串实际长度（递归计算）: %d\n", strLength(str));
    printf("字符串实际长度（strlen验证）: %ld\n", strlen(str));
    
    // 释放堆内存
    free(str);
    str = NULL;
    
    return 0;
}

原理说明：递归从字符串首字符开始，每递进一次移动到下一个字符，遇到'\0'时回归，累计的次数即为字符串长度。

4.计算斐波那契数列第n项的值

问题描述：用户通过键盘输入一个正整数n，设计递归函数计算斐波那契数列第n项的值（斐波那契数列定义：第1项和第2项均为1，从第3项开始，每一项等于前两项之和，即F(1)=1，F(2)=1，F(n)=F(n-1)+F(n-2)）。

实现代码：

/*******************************************************************
 *
*	file name:	Fibonacci.c
*	author	 :  str41379@163.com
 *	date	 :  2025/09/15
 *	function :  利用递归思想实现斐波那契数列第n项计算  考查递归思想解决问题
 * 	note	 :  None
 *
 *	CopyRight (c)  2024-2025   str41379@163.com   All Right Reseverd
 *
 * *****************************************************************/
#include <stdio.h>
#include <stdlib.h>

int Fibon(int n)
{
    // 终止条件：第1项和第2项均返回1
    if (1 == n || 2 == n)
    {
        return 1;
    }
    else
    {
        // 递归逻辑：第n项 = 第n-1项 + 第n-2项
        return Fibon(n - 1) + Fibon(n - 2);
    }
}

int main(int argc, char *argv[])
{
    // 定义指针变量用于指向堆内存，存储用户输入的n值
    int *ptr = NULL;
    // 申请1个int大小的堆内存并初始化为0
    ptr = (int *)calloc(1, 4); 
    if (NULL == ptr)
    {
        perror("堆内存申请失败！");
        return -1;
    }

    // 从键盘输入要计算的斐波那契数列项数
    printf("请输入你要求的第几项斐波那契数列的值:\n");
    scanf("%d", ptr);
    // 调用递归函数计算并输出结果
    printf("第%d项斐波那契数列的值为：%d\n", *ptr, Fibon(*ptr));
    // 释放堆内存，避免内存泄漏
    free(ptr);
    ptr = NULL;
    return 0;
}

原理说明：斐波那契数列的递归实现基于其数学定义，核心逻辑为F(n)=F(n-1)+F(n-2)，同时设置终止条件（n=1或n=2时返回1）避免无限递归。从计算流程来看，递归会逐层拆解问题：例如计算F(5)时，会先拆解为F(4)+F(3)，F(4)再拆解为F(3)+F(2)，F(3)拆解为F(2)+F(1)，直到触发终止条件（F(1)和F(2)均为1），最后通过“回归”过程将所有子问题的结果累加，最终得到F(5)=5的结果，其本质类似二叉树的叶子节点运算与结果回溯。

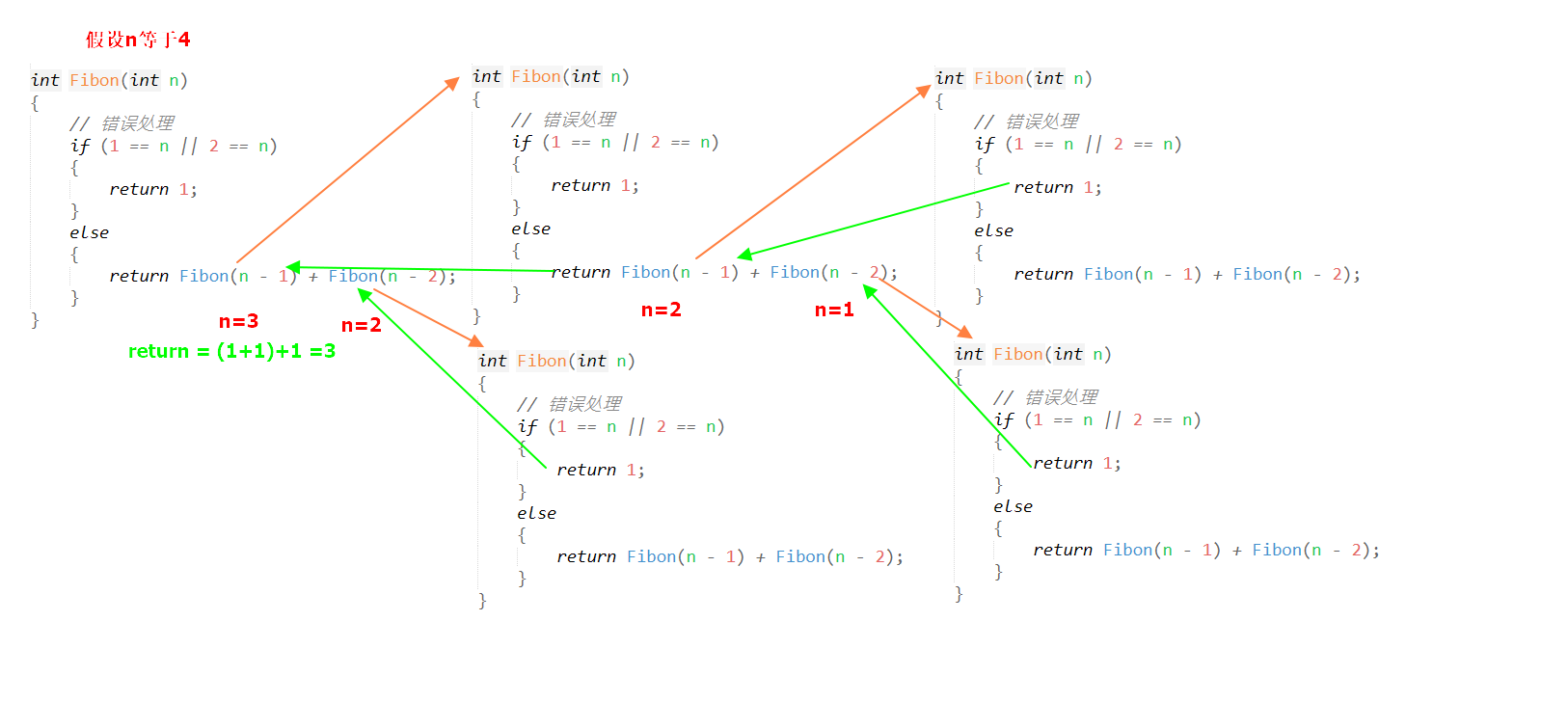
四、总结

递归思想通过将大问题分解为同类小问题，简化了代码实现，但需严格定义终止条件以避免栈溢出。上述代码例子展示了递归在数学计算、字符串处理等场景的应用，合理使用递归能有效提升代码的简洁性和逻辑性。