C语言中的查找与排序算法整理

查找与排序算法整理

1 查找算法

1.1 顺序查找

1.1.1 算法原理

顺序查找又称线性查找，是一种基本的查找算法，其原理是：

1. 从头开始遍历：从数据集的起始位置开始，逐个检查每个元素。
2. 比较目标：对于每个遍历到的元素，将其与目标元素进行比较。
3. 查找成功：如果当前元素等于目标元素，则查找成功，返回当前元素的索引。
4. 查找失败：如果遍历完整个数据集仍未找到目标元素，则查找失败，返回一个特殊的标识来表示未找到。

1.1.2 代码实现

/***********************************************************
 * 顺序查找
 * 时间复杂度： 最优O(1)、最高O(n)、平均O(n/2)
 * 空间复杂度： O(1)
 ***********************************************************/
#include <stdio.h>

/**
 * @brief 查找元素所在的位置
 * @param int *arr      数组
 * @param int len       数组长度
 * @param int target    要查找的元素
 * @return int 元素的位置，如果没有找到返回 -1
 */
int sequenceSearch(int *arr, int len, int target)
{
    for (int i = 0; i < len; i++)
    {
        if (arr[i] == target)
        {
            return i;
        }
    }
    return -1;
}


int main()
{
    int nums[6] = {10, 11, 7, 89, 23, 19};

    printf("7在数组中的位置：%d \n", sequenceSearch(nums,6, 7));
    printf("27在数组中的位置：%d \n", sequenceSearch(nums,6, 27));

    return 0;
}

1.2 二分查找

1.2.1 算法原理

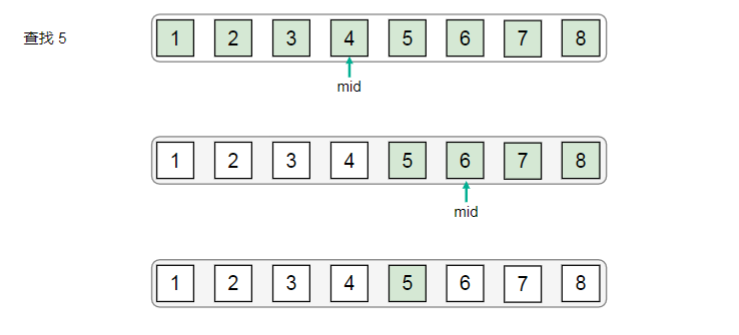
二分查找（Binary Search）是一种高效的搜索算法，通常用于有序数据集中查找目标元素。其原理是通过将数据集划分为两半并与目标进行比较，以确定目标在哪一半中，从而逐步缩小搜索范围，直到找到目标元素或确定不存在。基本原理如下：

1. 选择中间元素： 在有序数据集中，选择数组的中间元素。
2. 比较目标： 将中间元素与目标元素进行比较。
3. 查找成功： 如果中间元素等于目标元素，则查找成功，返回中间元素的索引。
4. 缩小搜索范围： 对于一个升序的数据集，如果中间元素大于目标元素，说明目标可能在左半部分；如果中间元素小于目标元素，说明目标可能在右半部分。根据比较结果，将搜索范围缩小到一半，继续查找。
5. 重复步骤： 重复上述步骤，不断将搜索范围缩小，直到找到目标元素或搜索范围为空。

1.2.2 代码实现

/***********************************************************
 * 二分查找
 ***********************************************************/
#include <stdio.h>

/**
 * @brief 查找元素所在的位置
 * @param int *arr      排好序数组
 * @param int len       数组长度
 * @param int target    要查找的元素
 * @return int 元素的位置，如果没有找到返回-1
 */
int binarySearch(int *arr, int len, int target)
{
    int start = 0;
    int end = len - 1;

    while (start <= end)
    {
        // 计算中间元素下标
        int mid = (start + end) / 2;

        // 判等
        if (arr[mid] == target)
        {
            return mid;
        }
        else if (target < arr[mid])
        {
            // 缩小搜索范围至左半部分
            end = mid - 1;
        }
        else if (target > arr[mid])
        {
            // 缩小搜索范围至右半部分
            start = mid + 1;
        }
    }

    return -1;
}

int main()
{
    int nums[] = {-10, 2, 8, 16, 109, 901, 5000};
    int len = sizeof(nums) / sizeof(int);

    printf("901在数组中的位置：%d \n", binarySearch(nums, len, 901));
    printf("901在数组中的位置：%d \n", binarySearch(nums, len, 3));

    return 0;
}

说明：二分查找的时间复杂度是 O(logn)，仅适用于有序数据集。

2 排序算法

2.1 十大常见的排序算法

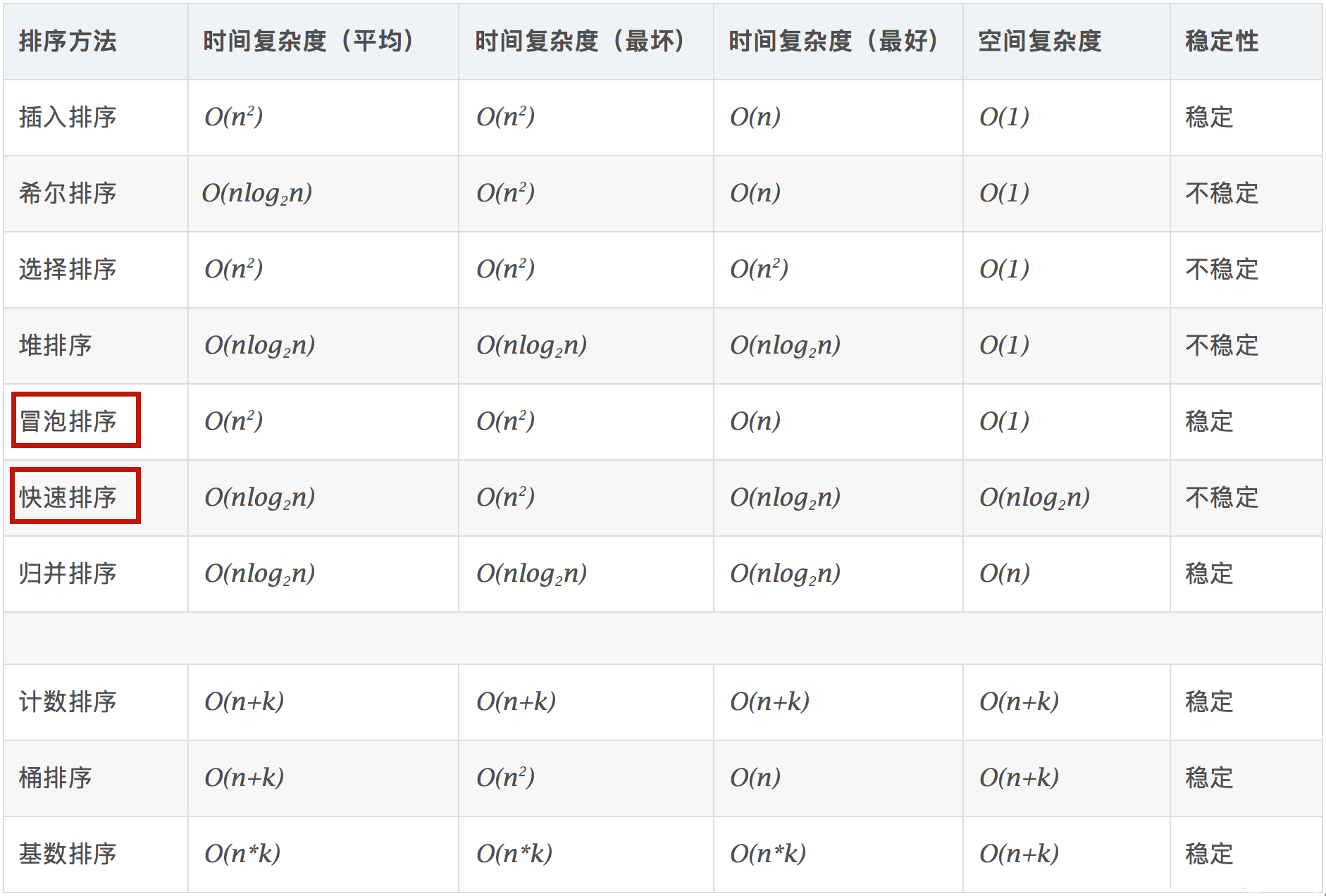
排序算法很多，实现方式各不相同，时间复杂度、空间复杂度、稳定性也各不相同：

2.2 冒泡排序

2.2.1 算法原理

冒泡排序原理如下：

1. 比较相邻元素： 从数组的第一个元素开始，依次比较相邻的两个元素。
2. 交换位置： 如果前面的元素比后面的元素大（或小，根据升序或降序排序的要求），则交换这两个元素的位置。
3. 一趟遍历完成后，最大（或最小）元素已移至末尾： 经过一趟遍历，最大（或最小）的元素会被交换到数组的最后一个位置。
4. 重复进行遍历和交换： 除了最后一个元素，对数组中的所有元素重复执行上述两步，每次遍历都会将当前未排序部分的最大（或最小）元素放置到合适的位置。
5. 循环遍历： 重复执行步骤 3 和步骤 4，直到整个数组都被排序。

2.2.2 代码实现

#include <stdio.h>

/**
 * @brief 交换两个变量或元素的值
 * @param int *a
 * @param int *b
 */
void swap(int *a, int *b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}

/**
 * @brief 定义函数 打印数组所有元素
 */
void printArr(int *arr, int len)
{
    for (int i = 0; i < len; i++)
    {
        printf("%d ", arr[i]);
    }
}

/**
 * @brief 冒泡排序
 * @param int *arr  要排序的数组
 * @param int len   数组长度
 */
void bubbleSort(int *arr, int len)
{
    // 外层循环 控制轮数 比较 len-1轮
    for (int n = 1; n < len; n++)
    {
        // 内层循环 控制本轮的比较
        for (int i = 0; i < len - n; i++)
        {
            // 如果前面的元素大，交换两个元素的值
            if (arr[i] > arr[i + 1])
            {
                swap(&arr[i], &arr[i + 1]);
            }
        }
    }
}

int main()
{
    // 定义数组
    int nums[8] = {30, 87, 23, 1023, 3, 5, 41, 2};
    int len = sizeof nums / sizeof(int);

    // 排序前
    printf("排序前：");
    printArr(nums, len);
    printf("\n");

    // 进行冒泡排序
    bubbleSort(nums, len);

    // 排序后
    printf("排序后：");
    printArr(nums, len);
    printf("\n");

    // // 第一轮比较
    // for (int i = 0; i < len - 1; i++)
    // {
    //     // 如果前面的元素大，交换两个元素的值
    //     if (nums[i] > nums[i + 1])
    //     {
    //         swap(&nums[i], &nums[i + 1]);
    //     }
    // }
    // printf("第一轮比较后：");
    // printArr(nums, len);
    // printf("\n");

    // // 第二轮比较
    // for (int i = 0; i < len - 2; i++)
    // {
    //     // 如果前面的元素大，交换两个元素的值
    //     if (nums[i] > nums[i + 1])
    //     {
    //         swap(&nums[i], &nums[i + 1]);
    //     }
    // }
    // printf("第二轮比较后：");
    // printArr(nums, len);
    // printf("\n");

    return 0;
}

说明：冒泡排序的平均时间复杂度为 O(n²)，空间复杂度为 O(1)，是一种稳定的排序算法，适用于小规模数据的排序场景。