[最优化理论与技术]预备知识

预备知识

目录

• 预备知识
  • 课程内容
  • 预备知识
  • 最优化问题
    • 数学表示
    • 分类
  • 多元函数的Taylor公式
    • 多元函数的梯度
    • 多元函数的极值与Hessian矩阵
    • 泰勒展开式
  • 凸集、凸函数和凸优化问题
    • 凸集
    • 凸函数
    • 凸优化
  • 补充内容
    • 仿射集 (affine set)
    • 锥 (cone)
    • 正定矩阵
    • 隐函数求导
    • 方向导数与梯度
    • 一维搜索的方法
    • 裴波那契法(Fibonacci法)
    • 黄金分割法
    • 牛顿法

课程内容

1. 预备知识
2. 线性规划
3. 一维搜索方法
4. 无约束最优化方法
5. 约束最优化方法
6. 工程应用优化

预备知识

1. 最优化问题
2. 多元函数的Taylor公式
3. 多元函数极值问题
4. 凸集、凸函数和凸优化
5. 算法相关概念
6. 算法概述

最优化问题

数学表示

\[minf(x)\\s.t \quad c(x)\ge 0 \]

• \(x=(x_1,x_2,...,x_n)\)是一个包含多变量的向量：决策变量
• \(c(x)\)是对各个变量约束的等式和不等式：约束条件
  • 可行域：约束条件在空间围成的区域
  • 可行解：可行域中每个点都是原问题的可行点
• \(f(x)\)：目标函数
  • 最优解：能使目标函数达到最大或最小的可行解

分类

按约束

• 无约束
• 有约束
  • 等式约束
  • 不等式约束

按目标函数

• 线性规划
• 非线性规划

按函数变量

• 整数规划
• 非整数规划

按目标函数个数

• 单目标优化
• 多目标优化

多元函数的Taylor公式

多元函数的梯度

偏导：多元函数降维时的变化，比如二元函数固定\(y\)，只让\(x\)单独变化，从而看成关于\(x\)的一元函数的变化

\[f_x(x,y)=lim_{\Delta x \to 0}\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x} \]

记作\(\frac{\partial f(x,y)}{\partial x}\)

梯度：多元函数在\(A\)点无数个变化方向中变化最快的那个方向；每一个变量都沿着关于这个变量的偏导所指定的方向来变化，函数的整体变化就能达到最大 (变化的绝对值最大) 。

\[gradA=(f_x(A),f_y(A),f_z(A)) \]

多元函数的极值与Hessian矩阵

参考Hessian矩阵与多元函数极值

一元函数极值问题：\(f(x)=x^2\)，先求一阶导数\(f'(x)=2x\)，根据费马定理极值点处的一阶导数一定等于0。

• 费马定理给出的是必要条件，由一阶导数=0可推出该店为极值，但不能由极值推出一阶导数=0
• 对该二次函数，一阶导数=0求得极值，但对\(f(x)=x^3\)，只检查一阶导数是不足以推出结果的
• 对\(f(x)=x^3\)，再求二阶导数，如果\(f''<0\)，说明函数在该点取得局部极大值；如果\(f''>0\)，说明函数在该点取得局部极小值；如果\(f''=0\)，说明结果任然不确定，需要其他方式确定函数极值

多元函数极值问题：\(f=f(x,y,z)\)，首先对每一个变量分别求偏导数，求得函数的可能极值点

\[\frac{\partial f}{\partial x}=0\\\frac{\partial f}{\partial y}=0\\\frac{\partial f}{\partial z}=0 \]

接下来，继续求二阶导数，包含混合偏导共9个偏导函数，用矩阵表示得到

\[H=\left[\begin{matrix}\frac{\partial ^2f}{\partial x \partial x} & \frac{\partial ^2 f}{\partial x \partial y } & \frac{\partial ^2 f}{\partial x \partial z } \\ \frac{\partial ^2f}{\partial y \partial x} & \frac{\partial ^2 f}{\partial y \partial y } & \frac{\partial ^2 f}{\partial y \partial z } \\ \frac{\partial ^2f}{\partial z \partial x} & \frac{\partial ^2 f}{\partial z \partial y } & \frac{\partial ^2 f}{\partial z \partial z}\end{matrix}\right] \]

矩阵\(H\)就是一个三阶Hessian矩阵。扩展到一般情况，对一个在定义域内二阶连续可导的实质多元函数\(f(x_1,x_2,...,x_n)\)定义其Hessian矩阵\(H\)如下

\[H=\left[\begin{matrix}\frac{\partial ^2f}{\partial x_1 \partial x_1} & \frac{\partial ^2 f}{\partial x_1 \partial x_2 } & \dots &\frac{\partial ^2 f}{\partial x_1 \partial x_n } \\ \frac{\partial ^2f}{\partial x_2 \partial x_1} & \frac{\partial ^2 f}{\partial x_2 \partial x_2 } & \dots & \frac{\partial ^2 f}{\partial x_2 \partial x_n } \\ \vdots & \vdots & \ddots & \vdots \\\frac{\partial ^2f}{\partial x_n \partial x_1} & \frac{\partial ^2 f}{\partial x_n \partial x_2 } & \dots & \frac{\partial ^2 f}{\partial x_n \partial x_n}\end{matrix}\right] \]

当一元函数的二阶导数=0，不能确定函数在该点的极值性。类似地，当Hessian矩阵行列式=0，也不能断定多元函数极值性的情况。甚至可能得到一个鞍点，也就是一个既非极大值也非极小值的点。

基于Hessian矩阵，可判断多元函数极值情况如下：

1. 如果Hessian矩阵是正定矩阵，则临界点处是一个局部极小值
2. 如果Hessian矩阵是负定矩阵，则临界点处是一个局部极大值
3. 如果Hessian矩阵是不定矩阵，则临界点处不是极值

判断矩阵是否正定：

1. 顺序主子式；实对称矩阵为正定矩阵的充要条件是的各顺序主子式都大于零
2. 特征值；实二次型矩阵为正定二次型的充要条件是的矩阵的特征值全大于零；负定二次型的充要条件是的矩阵的特征值全小于零；否则是不定的

泰勒展开式

一元函数的泰勒公式：设一元函数\(f(x)\)在包含点\(x_0\)的开区间\((a,b)\)内具有\(n+1\)阶导数，则当\(x \in (a,b)\)时，\(f(x)\)的\(n\)阶泰勒公式为：

\[f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+...+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_n(x) \]

其中，\(R_n(x)\)的拉格朗日余项表达形式

\[R_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}\quad \xi \in (x,x_0) \]

\(R_n(x)\)的皮亚诺余项表达形式

\[R_n(x)=o[(x-x_0)^n] \]

二元函数的泰勒公式：设二元函数\(z=f(x,y)\)在点\((x_0,y_0)\)的某一领域内连续且有直到\(n+1\)阶的连续偏导数，则有

\[f(x,y)=f(x_0,y_0)+[(x-x_0)\frac{\partial}{\partial x}+(y-y_0)\frac{\partial}{\partial y}]f(x_0,y_0)+\\ \frac{1}{2!}[(x-x_0)\frac{\partial}{\partial x}+(y-y_0)\frac{\partial}{\partial y}]^2f(x_0,y_0)+...\\ +\frac{1}{n!}[(x-x_0)\frac{\partial}{\partial x}+(y-y_0)\frac{\partial}{\partial y}]^nf(x_0,y_0)\\+R_n(x,y) \]

其中，记号

\[(x-x_0)\frac{\partial}{\partial x}+(y-y_0)\frac{\partial}{\partial y}]f(x_0,y_0) \]

表示

\[(x-x_0)f_x(x_0,y_0)+(y-y_0)f_y(x_0,y_0) \]

记号

\[[(x-x_0)\frac{\partial}{\partial x}+(y-y_0)\frac{\partial}{\partial y}]^2f(x_0,y_0) \]

表示

\[(x-x_0)^2f_{xx}(x_0,y_0)+2(x-x_0)(y-y_0)f_{xy}(x_0,y_0)+(y-y_0)^2f_{yy}(x_0,y_0) \]

一般地，记号

\[[(x-x_0)\frac{\partial}{\partial x}+(y-y_0)\frac{\partial}{\partial y}]^mf(x_0,y_0) \]

表示

\[\sum_{p=0}^m C_m^p(x-x_0)^p(y-y_0)^{(m-p)} \frac{\partial^m f}{\partial x^p\partial y^{(m-p)}}|_{(x_0,y_0)} \]

用一般化表达式重写上面的式子

\[f(x,y)=\sum_{k=0}^n\frac{1}{k!}[(x-x_0)\frac{\partial}{\partial x}+(y-y_0)\frac{\partial}{\partial y}]^kf(x_0,y_0)\\ +R_n(x,y) \]

拉格朗日余项为：

\[R_n(x,y)=\frac{1}{(n+1)!}[(x-x_0)\frac{\partial}{\partial x}+(y-y_0)\frac{\partial}{\partial y}]^{(n+1)}f(x_0+\theta(x-x_0),y_0+\theta(y-y_0))\\\theta \in (0,1) \]

皮亚诺余项为：

\[R_n(x,y)=o(\rho^n) \]

Hessian矩阵与泰勒展开的关系：对于一个多维向量\(X\)，多元函数\(f(X)\)在点\(X_0\)的领域内有连续二阶偏导数，可写出\(f(X)\)在点\(X_0\)处的二阶泰勒展开式

\[f(\mathbf{X})=f(\mathbf{X}_0)+(\mathbf{X}-\mathbf{X}_0)^T\nabla f(\mathbf{X}_0)+\frac{1}{2!}(\mathbf{X}-\mathbf{X}_0)^T\nabla^2 f(\mathbf{X}_0)(\mathbf{X}-\mathbf{X}_0)+o(\|\mathbf{X}-\mathbf{X}_0\|^2) \]

而\(\nabla^2 f(\mathbf{X}_0)\)显然是一个Hessian矩阵，所以可写成：

\[f(\mathbf{X})=f(\mathbf{X}_0)+(\mathbf{X}-\mathbf{X}_0)^T\nabla f(\mathbf{X}_0)+\frac{1}{2}(\mathbf{X}-\mathbf{X}_0)^T\mathbf{H}(\mathbf{X}_0)(\mathbf{X}-\mathbf{X}_0)+o(\|\mathbf{X}-\mathbf{X}_0\|^2) \]

1. 多元函数取得极值的必要条件：\(u=f(x_1,x_2,...,x_n)\)在点\(M\)处有极值，则有

   \[\nabla f(M)=\left \{\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\cdots, \frac{\partial f}{\partial x_n}\right\}_M=0 \]

2. 多元函数取得极值的充分条件：其二阶偏导组成的Hessian矩阵为正定(局部极小值)or负定(局部极大值)

凸集、凸函数和凸优化问题

凸集

集合\(C\)内任意两点间的线段也在集合\(C\)内，则称集合\(C\)为凸集:

\[\lambda x +(1-\lambda)y \in C\quad for \quad \forall \lambda \in (0,1),\quad \forall(x,y)\in C \]

凸函数

定义在凸集\(C\)上的凸函数：

\[f(\lambda x_1+(1-\lambda)x_2)\le \lambda f(x_1)+(1-\lambda)f(x_2) \\x_1,x_2 \in C;\quad \lambda \in (0,1) \]

凸优化

机器学习主要做的就是优化问题，先初始化一下权重参数，然后利用优化方法来优化权重，直到准确率不再上升，迭代停止。在优化问题中，应用最广泛的是凸优化问题：

• 若可行域是凸集
• 且目标函数是一个凸函数

则这样的优化问题是凸优化问题

补充内容

仿射集 (affine set)

欧式空间 \(R^n\) 中的点集 \(M\)，对于\(\forall x,y \in M\)，以及 \(\forall \lambda\)，总有：

\[(1-\lambda)x+\lambda y \in M \]

则点集 \(M\) 是仿射集。

几何意义：仿射集的几何意义是：一个集合中任意两点的连线上的点仍然属于这个集合。（在三维空间内，整个坐标系才属于仿射集）

例：

• 三维欧氏空间 \(R^3\) 中，直线和平面都是仿射集，空集 \(\varnothing\) 也是仿射集
• \(S\) 是 \(R^n\) 中的子空间的充要条件是 \(S\) 是包含原点的仿射集
• 每一非空仿射集 \(S\) 都平行于唯一子空间 \(L\)
  • 集合平移：\(S+p=\{ x+p|x \in S \}\)
• 非空仿射集 \(S\) 的维数是与它平行的子空间的维数，\(dim(S)\)
• 维数为 0，1，2 的仿射集就是熟知的点、线、面
• \(R^n\) 中的 \(n-1\) 维仿射集称为超平面 (hyperplane)

锥 (cone)

参考：锥，凸锥，二阶锥，二阶锥规划

对于一个向量空间 \(V\) 与它的一个子集 \(C\)，如果子集 \(C\) 中任意一点 \(x\) 与任意正数 \(a\)

，其乘积 \(ax\) 仍然属于子集 \(C\)，则称 \(C\) 为一个锥。

锥总是无界的。

凸锥：锥 \(C\) 中任意两点 \(x\) 和 \(y\)，\(ax+by \in C\quad(a,b>0)\)

• 凸锥首先是凸集
• 不是凸锥的锥，eg：\(y=|x|\)，但是 \(y \ge |x|\) 就是凸锥

正定矩阵

• 对于 \(n*n\) 实对称矩阵： \(M\)满足任意非零实系数向量 \(x\)，都有 \(x^TMx>0\)，则 \(M\) 是正定的
• 对于复数矩阵：一个 \(n*n\) 的 \(Hermite\) 矩阵 \(M\) 是正定的当且仅当任意非零复向量 \(x\)，都有 \(x^HMx>0\)。
  • 前提要是 \(Hermite\) 矩阵，满足 \(M^H=M\)

隐函数求导

隐函数：如果方程 $F(x,y=0) $ 能确定 \(y\) 是 \(x\) 的函数，那么称这种函数表达方式为隐函数。(已知函数关系，不容易写出显函数形式)

1. 表示成关于 \(y\) 的函数，链式求导
2. 将待求导变量放到等式一边，等式两边同时求导
3. 隐函数保存不变，直接对等式两边求导

方向导数与梯度

参考：[梯度下降（Gradient Descent）小结]

一维搜索的方法

Line Search (一维搜索，或线搜索、一维优化) 是最优化 (Optimization) 算法中的一个基础步骤，是求解一维目标函数 \(f(x)\) 最优解的过程。可以分为精确的一维搜素和不精确的一维搜素两大类。

当采用数学规划法寻求多元函数极值点时，一般需进行如下格式的迭代计算：$$x^{k+1}=x+\alpha_ks^k(k=0,1,2,...)$$

当方向 \(s^k\) 给定，求最佳步长 \(\alpha_k\) 就是求一元函数：

\[f(x^{k+1})=f(x^k+\alpha_ks^k)=\phi(\alpha_k) \]

的极值问题，这一过程被称为一维搜索

裴波那契法(Fibonacci法)

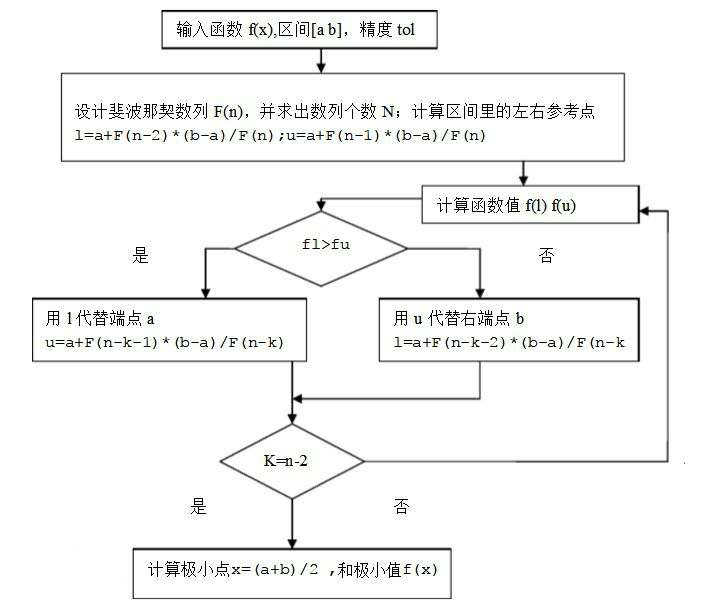
在区间 \([a,b]\) 内取两个不同点，算出函数值加以比较，逐步缩小搜索区间。

单峰函数

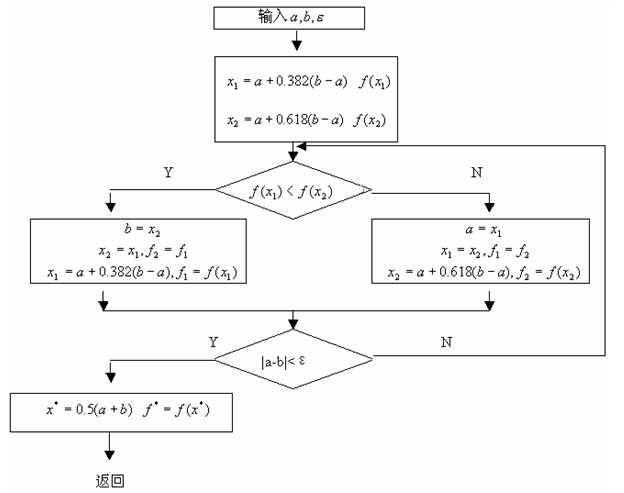
黄金分割法

牛顿法

切线是曲线的线性逼近

多次迭代后会越来越接近曲线的根

对于非线性函数 \(f(x)\)，根据泰勒公式得到 \(x\) 附近某个点\(x_{k}\)展开的多项式可用来近似函数 \(f(x)\) 的值，该多项式对应的函数为 \(F(x)\)，求得 \(F(x)\) 的极小值作为新的迭代点，然后继续在新的迭代点泰勒公式展开，直到求得的极小值满足一定的精度。

原理：

假设函数 \(f(x)\) 二次可微，则二阶泰勒展开：

\[f(x)\approx g(x)=f(x_k)+f'(x_k)(x-x_k)+\frac{1}{2}f''(x_k)(x-x_k)^2 \]

\(g(x)\) 与 \(f(x)\) 近似，求函数 \(f(x)\) 的极值转化为求导函数为0，对 \(g(x)\) 求导并令等于0，

\[f'(x_k)+f''x_k(x-x_k)=0 \]

得：

\[x=x_k-\frac{f'(x_k)}{f''(x_k)} \]

得迭代公式：

\[x_{k+1}=x_k-\frac{f'(x_k)}{f''(x_k)} \]

代码：

参考：机器学习之牛顿法

def h(x):
    return x*x*x + 2*x*x +3*x + 4

def h1(x):
    return 3*x*x + 4*x + 3

def h2(x):
    return 6*x + 4

xk = 0
k = 1
y = 0
e = 0.0001
times = 10000

while k < times:
    y = h(xk)
    a = h1(xk)
    if abs(a) <= e:
        break
    b = h2(xk)
    xk -= a/b
    k += +1
print("k = ", k)
print("x = ", xk)
print("y = ", y)