牛客刷题-Day24

牛客刷题-Day24

今日刷题：\(1046-1050\)

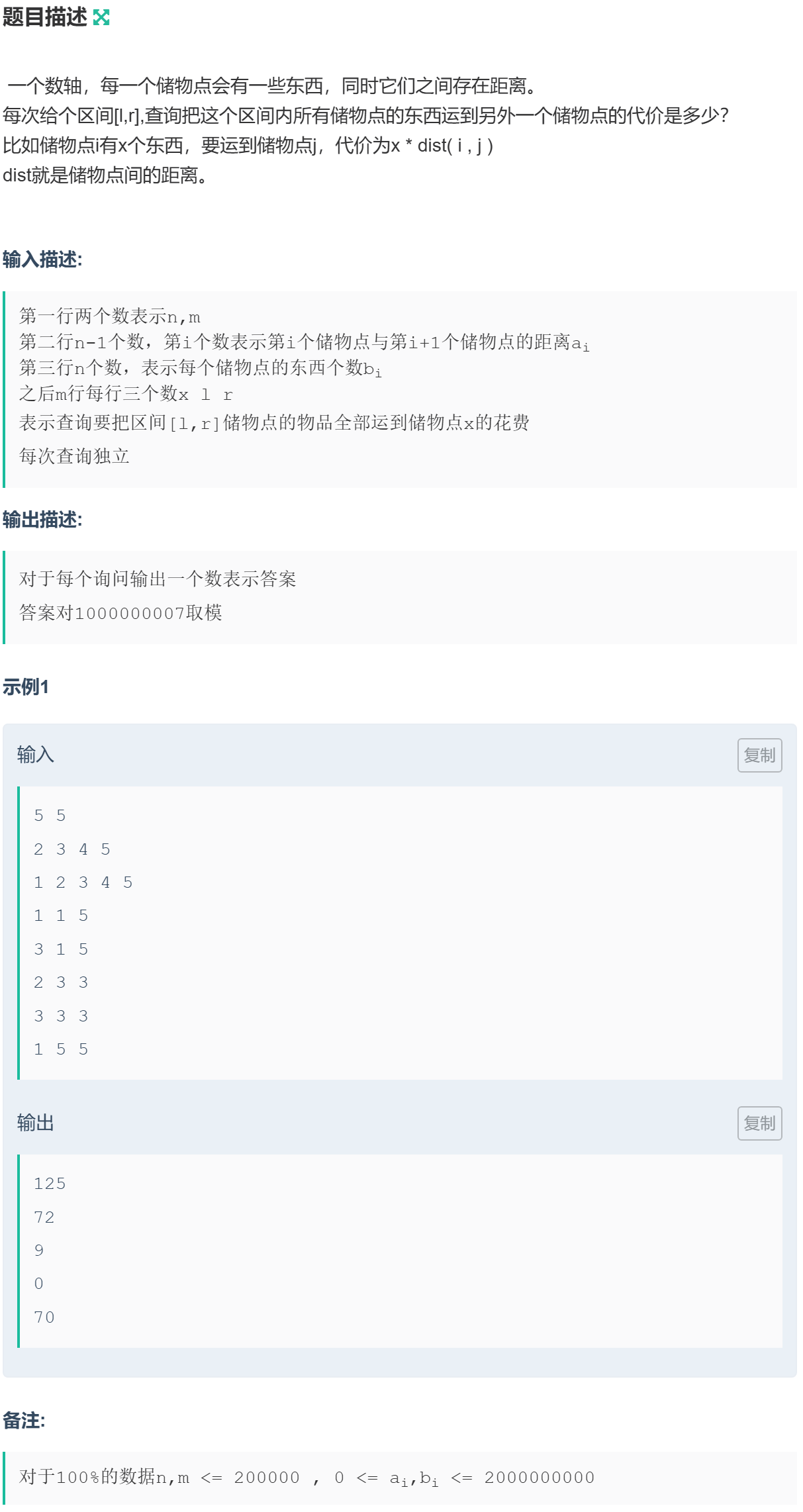
1048 习题-储物点的距离

解题思路

对于 \(i\in[l,r]\)，将 \(i\) 处的物品运输到 \(x\) 处，代价为 \(b_i*|pos_i-pos_x|\)，即物品数量与距离的乘积，然后累加。
计算时，分类讨论 \(x\) 在区间 \([l,r]\) 的位置，以便于去除绝对值符号。
此外，从 \(i\) 到 \(x\) 处的代价，也等价于 \(i\) 到 \(1\) 处与 \(x\) 到 \(1\) 处代价的差值，因此预处理出前 \(i\) 处物品运输到 \(1\) 的代价之和。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 200010, MOD = 1000000007;
typedef long long LL;

int n, m;
LL a[N], b[N], cost_to_1[N]; // 距离前缀和、物品前缀和、到位置 1 代价前缀和

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 2; i <= n; i++) {
        scanf("%lld", &a[i]);
        a[i] = (a[i] + a[i - 1]) % MOD;
    }
    for (int i = 1; i <= n; i++) {
        scanf("%lld", &b[i]);
        cost_to_1[i] = (cost_to_1[i - 1] + b[i] * a[i] % MOD) % MOD;
        b[i] = (b[i] + b[i - 1]) % MOD;
    }
    LL ans = 0;
    while (m--) {
        int x, l, r;
        scanf("%d%d%d", &x, &l, &r);
        if (x <= l) {
            LL c = (cost_to_1[r] - cost_to_1[l - 1] + MOD) % MOD;
            LL d = ((b[r] - b[l - 1] + MOD) % MOD) * a[x] % MOD;
            ans = (c - d + MOD) % MOD;
        } else if (x >= r) {
            LL c = (cost_to_1[r] - cost_to_1[l - 1] + MOD) % MOD;
            LL d = ((b[r] - b[l - 1] + MOD) % MOD) * a[x] % MOD;
            ans = (d - c + MOD) % MOD;
        } else {
            LL c = (cost_to_1[x] - cost_to_1[l - 1] + MOD) % MOD;
            LL d = ((b[x] - b[l - 1] + MOD) % MOD) * a[x] % MOD;
            LL e = (cost_to_1[r] - cost_to_1[x] + MOD) % MOD;
            LL f = ((b[r] - b[x] + MOD) % MOD) * a[x] % MOD;
            ans = ((d - c + MOD) % MOD + (e - f + MOD) % MOD) % MOD;
        }
        printf("%lld\n", ans);
    }
    return 0;
}

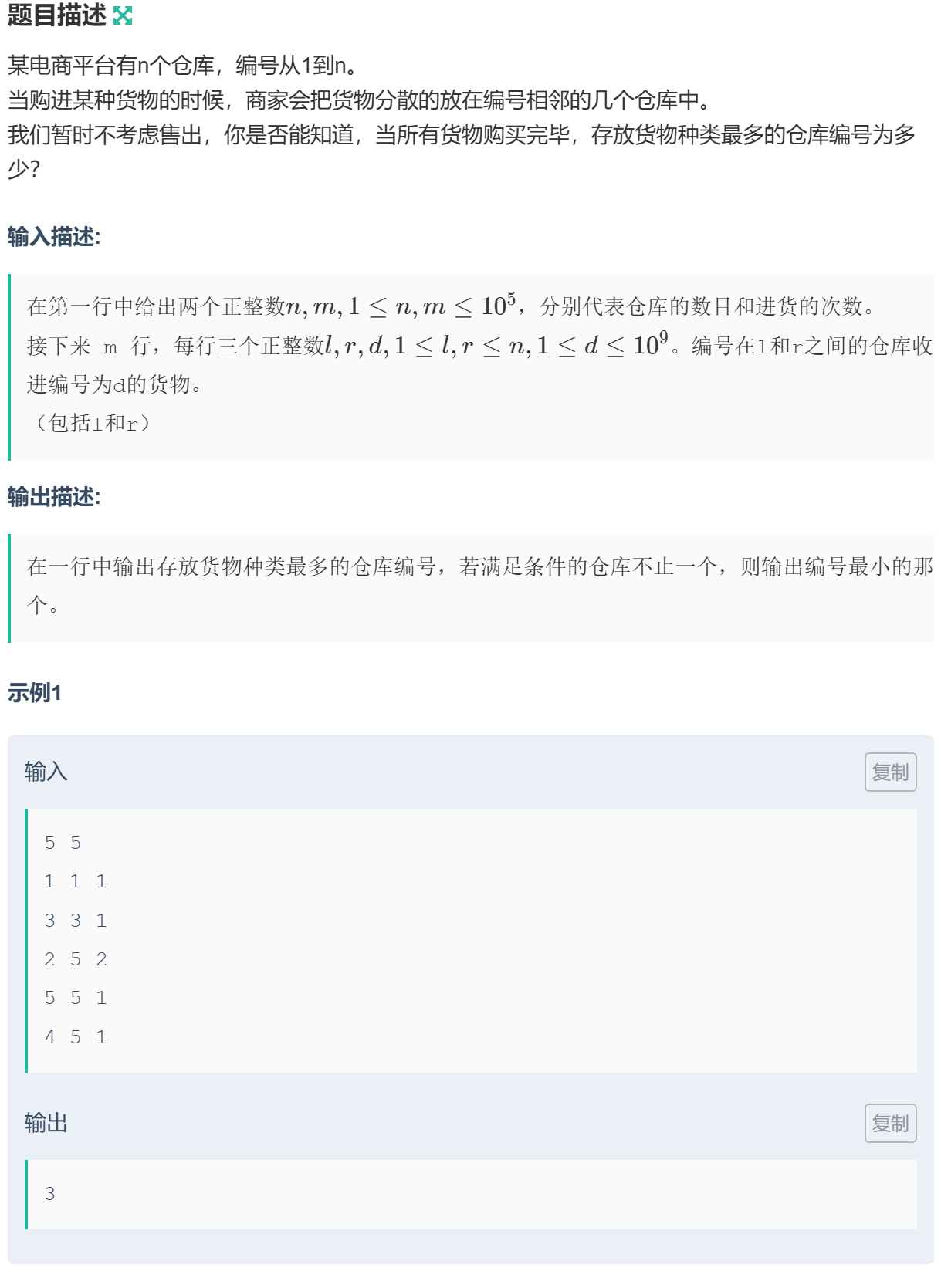
1049 习题-货物种类

解题思路

按照货物编码和区间进行排序。
对于同一个货物编码，将其重叠区间进行合并，以防止重复计算。
区间计算用差分和前缀和处理。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 100010;

int n, m;
struct Node {
    int l, r, d;
} a[N];
int s[N];


bool cmp(Node a, Node b) {
    if (a.d == b.d) {
        if (a.l == b.l)
            return a.r < b.r;
        return a.l < b.l;
    }
    return a.d < b.d;
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; i++)
        scanf("%d%d%d", &a[i].l, &a[i].r, &a[i].d);
    sort(a + 1, a + m + 1, cmp);
    int st = a[1].l, ed = a[1].r;
    for (int i = 2; i <= m; i++) {
        if (ed >= a[i].l && a[i].d == a[i - 1].d) {
            ed = max(ed, a[i].r);
        } else {
            s[st]++, s[ed + 1]--;
            st = a[i].l, ed = a[i].r;
        }
    }
    s[st]++, s[ed + 1]--;
    int mx = 0, res = 0;
    for (int i = 1; i <= n; i++) {
        s[i] += s[i - 1];
        if (s[i] > mx) {
            mx = s[i], res = i;
        }
    }
    printf("%d\n", res);
    return 0;
}

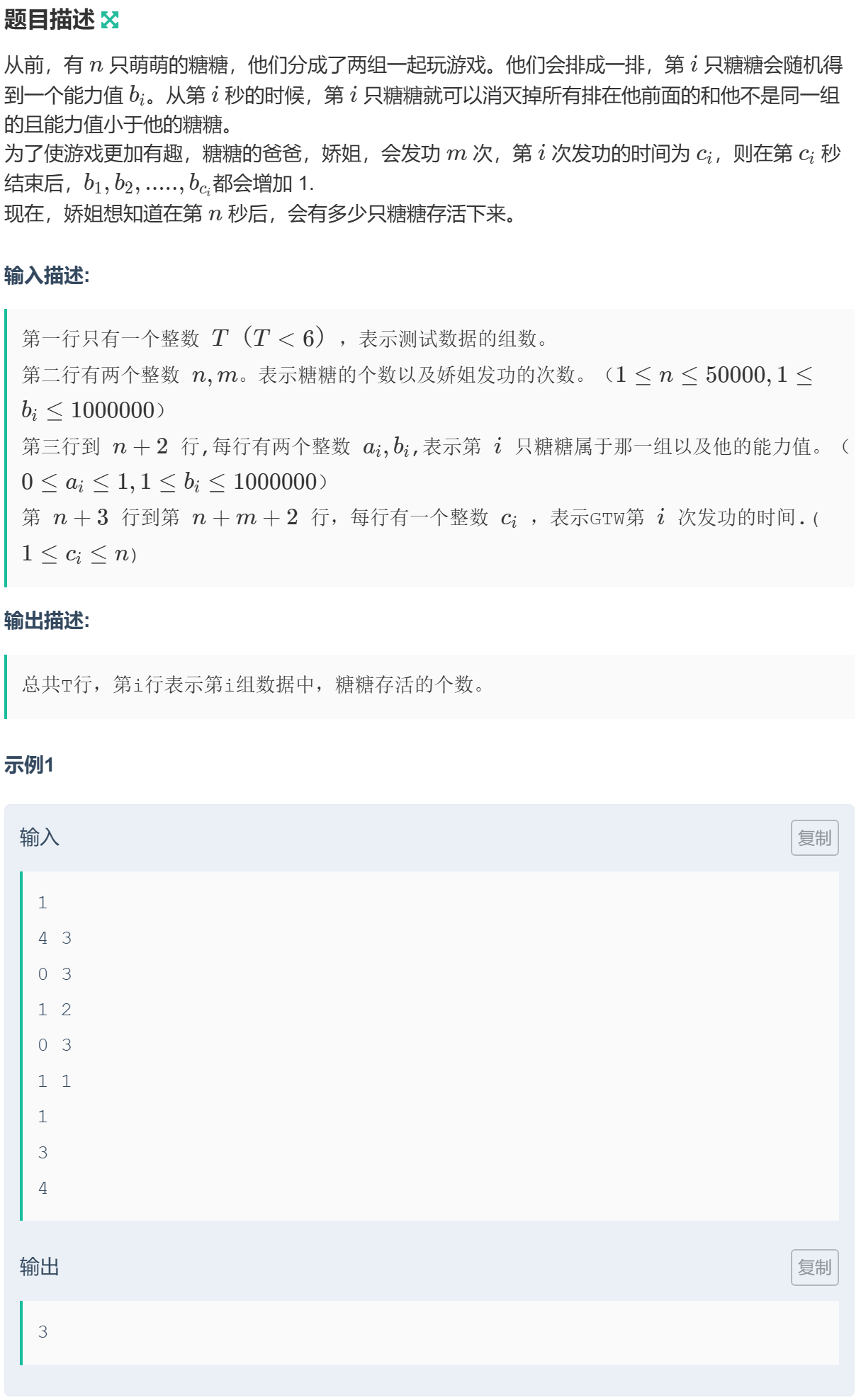
1050 习题-糖糖别胡说，我真的不是签到题目

解题思路

一只糖糖存活下来，只需要看其右侧有无和它不同组且能力值大于它的糖糖，如果存在，则该糖糖无法存活。基于此，考虑从右往左遍历解决问题，需要两个额外变量来记录到当前位置时两个组的能力值的最大值。
发功的过程使用差分数据来模拟，最后的能力值就是初始值加上变化值。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 50010;

int T;
int n, m;
int a[N], b[N], d[N];

int main() {
    scanf("%d", &T);
    while (T--) {
        memset(d, 0, sizeof d);
        scanf("%d%d", &n, &m);
        for (int i = 1; i <= n; i++)
            scanf("%d%d", &a[i], &b[i]);
        for (int i = 0; i < m; i++) {
            int c;
            scanf("%d", &c);
            d[c]++;
        }
        int delta = 0, res = n, mx0 = 0, mx1 = 0;
        for (int i = n; i; i--) {
            delta += d[i];
            if (a[i]) {
                res -= (b[i] + delta) < mx0;
                mx1 = max(b[i] + delta, mx1);
            } else {
                res -= (b[i] + delta) < mx1;
                mx0 = max(b[i] + delta, mx0);
            }
        }
        printf("%d\n", res);
    }
    return 0;
}