4815: [Cqoi2017]小Q的表格 莫比乌斯反演 分块
(Updated 2018.04.28 : 发现公式效果不好,重新处理图片)
国际惯例的题面: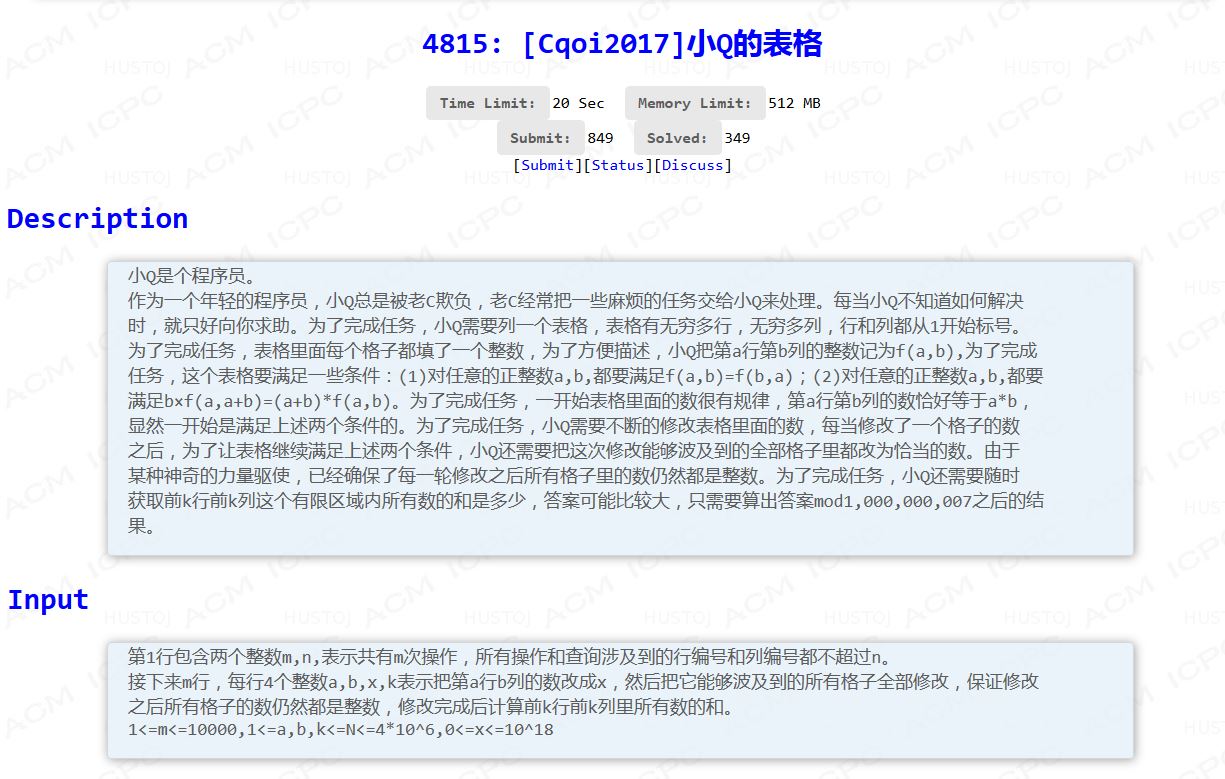
看到这两个公式,很多人都会想到与gcd有关。没错,最终的结论就是f(a,b)=f(gcd(a,b))*(a/gcd(a,b))*(b/gcd(a,b))。然而结论只能猜出来是不行的,我们考虑如何证明他。
网上很多大神的构造性证明已经很清楚了,然而我太菜,不会构造,让我们来一发非构造性证明。
由于:
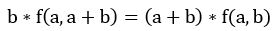
我们设x=a+b,则b=x-a,显然我们有前提条件x≠a。
用x替换b,得:

我们移项,得:
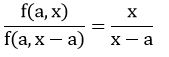
如果x≥2*a,我们可以继续迭代:

如果我们让上面两个等式相乘,会发现:
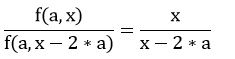
显然迭代下去,我们会有:
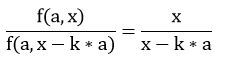
如果x=p*a,我们令k=p-1,我们有:

如果我们令k=(x/a)(下取整),我们有:
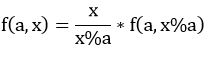
然而我们现在连右边那个东西能否整除都不知道……没关系,继续展开等式。
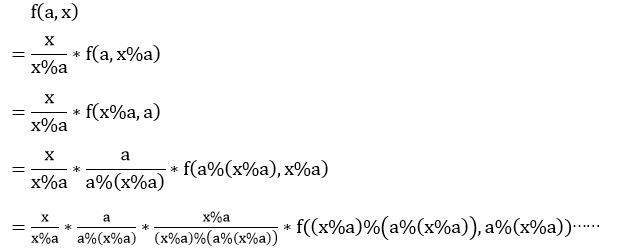
我们看到了一个非常愉悦的事情:两个x%a约掉了。
仔细观察,会发现分子上的东西是f的第二个参数的连乘积,分母上的东西是f的第二个参数取模第一个参数的连乘积(废话)。
考虑我们一直迭代下去,最终会剩下什么。
迭代终止的条件是x%a=0,这时候我们带入前面推出x=p*a时适用的公式,的那个这样会剩下分子的前两项和分母的最后两项。
显然分子剩下的前两项为x和a,分母剩下的最后一项为gcd(a,b),而根据上面迭代的等式,分母的倒数第二项为倒数第二次带入f()的第一个参数,显然也是gcd(a,b)。
至此我们的结论得证(一个证明搞这么麻烦,我好蒻啊)。
然后就是计算的问题。
我们要求的是:
如果我们能够预处理出g(),O(sqrt(n))修改并O(1)查询f()的前缀和,我们就能在sqrt(n)的复杂度内完成每次操作。
显然维护f()直接大力块状数组即可,重点是g()。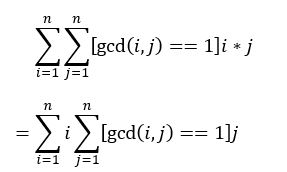
这里有一个很优美的结论,就是
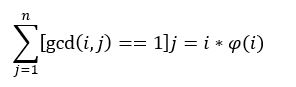
然后我们就有: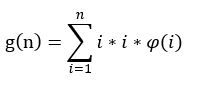
之后线性筛φ就好了。
代码(老年选手已经毫不畏惧卡常数):

1 #include<cstdio> 2 #include<algorithm> 3 #include<cmath> 4 #define bool unsigned char 5 #define debug cout 6 typedef long long int lli; 7 const int maxn=4e6+1e2,maxb=2e3+1e2; 8 const int mod=1e9+7; 9 10 lli phi[maxn]; 11 int n,m; 12 13 inline lli fastpow(lli base,int tim) { 14 lli ret = 1; base %= mod; 15 while(tim) { 16 if( tim & 1 ) ret = ret * base % mod; 17 if( tim >>= 1 ) base = base * base % mod; 18 } 19 return ret; 20 } 21 inline int gcd(int x,int y) { 22 register int t; 23 while( ( t = x % y ) ) x = y , y = t; 24 return y; 25 } 26 27 namespace Pre { 28 inline void sieve() { 29 static int prime[maxn],cnt; 30 static bool vis[maxn]; 31 phi[1] = 1; 32 for(int i=2;i<=n;i++) { 33 if( !vis[i] ) prime[++cnt] = i , phi[i] = i - 1; 34 for(int j=1;j<=cnt&&(lli)i*prime[j]<=n;j++) { 35 const int tar = i * prime[j]; 36 vis[tar] = 1; 37 if( i % prime[j] ) phi[tar] = phi[i] * ( prime[j] - 1 ); 38 else { 39 phi[tar] = phi[i] * prime[j]; 40 break; 41 } 42 } 43 } 44 for(int i=1;i<=n;i++) phi[i] = ( phi[i] * i % mod * i % mod + phi[i-1] ) % mod; 45 } 46 } 47 48 struct BlockedArrary { 49 lli dat[maxn],sumins[maxn],blk[maxb],sumblk[maxb]; 50 int bel[maxn],st[maxb],ed[maxb],blksiz,cnt; 51 52 inline lli query(int pos) { 53 return pos ? ( sumblk[bel[pos]-1] + sumins[pos] ) % mod : 0; 54 } 55 inline void update(int pos,lli val) { 56 dat[pos] = val; 57 int id = bel[pos] , l = st[id] , r = ed[id]; 58 sumins[l] = dat[l]; for(int i=std::max(pos,l+1);i<=r;i++) sumins[i] = ( sumins[i-1] + dat[i] ) % mod; 59 blk[id] = sumins[r]; for(int i=id;i<=cnt;i++) sumblk[i] = ( sumblk[i-1] + blk[i] ) % mod; 60 } 61 inline void init() { 62 for(int i=1;i<=n;i++) dat[i] = (lli) i * i % mod; 63 blksiz = std::sqrt(n); 64 for(int l=1,r;l<=n;l=r+1) { 65 r = std::min( l + blksiz - 1 , n ) , ++cnt , st[cnt] = l , ed[cnt] = r , sumins[l] = dat[l]; 66 for(int i=l;i<=r;i++) bel[i] = cnt; 67 for(int i=l+1;i<=r;i++) sumins[i] = ( sumins[i-1] + dat[i] ) % mod; 68 sumblk[cnt] = ( sumblk[cnt-1] + ( blk[cnt] = sumins[r] ) ) % mod; 69 } 70 } 71 }ba; 72 73 inline void update(int a,int b,lli d) { 74 int g = gcd(a,b); 75 lli tv = d % mod * fastpow((lli)a*b/g/g,mod-2) % mod; 76 ba.update(g,tv); 77 } 78 79 inline lli query(int k) { 80 lli ret = 0; 81 for(int i=1,j;i<=k;i=j+1) { 82 j = k / ( k / i ); 83 ret = ( ret + ( ba.query(j) - ba.query(i-1) + mod ) % mod * phi[k/i] % mod ) % mod; 84 } 85 return ret; 86 } 87 88 int main() { 89 static int a,b,k; 90 static lli x; 91 scanf("%d%d",&m,&n) , Pre::sieve() , ba.init(); 92 while(m--) scanf("%d%d%lld%d",&a,&b,&x,&k) , update(a,b,x) , printf("%lld\n",query(k)); 93 return 0; 94 }
過去の想い 記憶の彼方
过往的思念 记忆中的远方
幼き日 残した悔い
稚气时光中 所留下的懊悔
胸の奥 刻む針音(しんおん)
内心深处 铭刻下心音
心だけ 置き忘れたまま
让它留在心里慢慢被遗忘吧



 浙公网安备 33010602011771号
浙公网安备 33010602011771号