常见字符串算法
本文主要讲解 Manacher,后缀数组 SA,KMP,Z Algorithm(exKMP)。
KMP 算法
1.1 KMP简介
kmp算法,是一种线性字符串匹配(父子串为 root,子子串为 s),由 D.E.Knuth,J.H.Morris 和 V.R.Pratt 提出的,因此人们称它为KMP算法。
1.2 暴力思路
举个样例吧。
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| root | a | b | c | a | a | b | c | a | b |
| s | a | b | c | a | b |
拿到这个串,我们让两个指针 \(l,r\) 分别指向 \(root\) 和 \(s\)。
共 \(len(root)\) 轮,对于第 \(i\) 轮,让 \(l\gets i,r\gets 1\),并执行按顺序执行以下操作:
- 如果 \(r=len(s)\) 则找到 \(s\)。
- 如果 \(r\ne len(s)\) 且 \(root_l=s_r\),则 \(l\gets l+1,r\gets r+1\),并重复该操作。
- 如果 \(root_l\ne s_r\),则跳过该阶段。
就拿样例而言,对于第 \(1\) 轮,\(l=1,r=1\),发现 \(root_1=s_1\),则 \(l+1,r+1\)。当 \(l=5,r=5\) 时,\(root_5\ne s_5\),则进行第2轮,\(l=2,r=1\)......
你会发现,一旦中途不符合条件,已知的信息最会浪费。那有没有不浪费已知信息的算法呢?
虽然哈希也可以解决此类方法,但是KMP算法可以获得更多信息。
1.3 KMP算法
1.3.1 过程
再来举个样例:
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| root | A | B | C | D | A | B | C | D | A | B | C | E |
| s | A | B | C | D | A | B | C | E |
我们匹配好前面八位的时候,发现第九位不对,我们就移动 \(s\),根据前面已知的,我们就可以像下面这样:
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| root | A | B | C | D | A | B | C | D | A | B | C | E |
| s | A | B | C | D | A | B | C | E |
直接向后移动四位,然后我们的 \(l\) 继续从第五位开始,直到匹配成功。
注意:我们都是判断 \(l\) 和 \(r\) 下一个位置是否为相同。
前缀串与后缀串
如 abcde:
前缀串:a,ab,abc,abcd,abcde
后缀串:e,de,cde,bcde,abcde
其实,\(r\) 只是回跳到使得 \(root\) 前 \(l\) 段的后缀与 \(s\) 前 \(r\) 段的前缀相等的最长长度的位置(除了自己),有点长,大家可以分开理解。
例如,当 \(l=8,r=8\) 时,下一个位置不一样,则将 \(r\) 回退到 \(3\),因为 \(root\) 前 \(8\) 个中的倒数 \(3\) 个与 \(s\) 前 \(4\) 个中的前面 \(3\) 个一样都是 \(ABC\),所以回退到 \(3\)。
这里,我们为了预处理,简化一下,来发下一下性质。还是这个例子:
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| root | A | B | C | D | \(\red{A}\) | \(\red{B}\) | \(\red{C}\) | D | A | B | C | E |
| s | \(\green{A}\) | \(\green{B}\) | \(\green{C}\) | D | \(\purple{A}\) | \(\purple{B}\) | \(\purple{C}\) | E |
我们要用到的是红色和绿色的字母,这里就是最长公共前后缀。但是,大家想一想,紫色部分和红色部分是不是一模一样的呀,因为指针能到 \(7\),肯定是因为紫色部分和红色部分一样。
那这样子,紫色和红色一样,红色和绿色一样,那绿色就和紫色一样!这样,我们就只需要预处理 \(s\) 就可以了。
1.3.2 具体实现
到这里,我们可以写出伪代码(\(next\) 为 \(s\) 的最长公共前后缀):
if root[l] = s[r] then
l <- l + 1, r <- r + 1
else then
r <- next[r]
那怎么预处理 \(next\) 呢?再举一个例子:
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| s | a | b | a | b | \(\red{e}\) | f | a | b | a | b | _ |
next[0]=0
next[1]=0
next[2]=0
next[3]=1
next[4]=2
next[5]=0
next[6]=0
next[7]=1
next[8]=2
next[9]=3
next[10]=4
我们试着用已知信息求未知信息,已知 \(next_{1\sim10}\),求 \(next_{11}\)。
已知:\(s_{1\sim4}=s_{7\sim10}\)。
- 如果 \(s_5=s_{11}=e\),那么 \(next_{11}=next_{10}+1\)。
- 如果 \(s_{11}=a\),那么,取次长公共前后缀,就是 \(ab\),长度为 \(2\),就是 \(next_{next_{10}}\),刚好可以与 \(a\) 搭配,形成 \(aba\),则 \(next_{11}=next_{next_{10}}+1=3\)。
- 如果 \(s_{11}=x\),什么都不是,那就只能是 \(0\)了。可以转化为不断地取次长公共前后缀,但是都不符合,最后变成 \(0\) 了而已。
综上,我们得出,只要 \(s_{i+1}\ne s_{r+1}\),就让 \(r\gets next_r\),前提是 \(r\ne0\)。
最后就让 \(next_{i+1}=next_{r}+1\) 就行咯。
代码:
inline void init() {
nex[0] = nex[1] = 0; // 初始化
int m = t.size();
for (int i = 1, j = 0; i < m; i++) { // 求 nex[i+1]
while (j && s[i + 1] != s[j + 1]) j = nex[j]; // 取次长
if (s[i + 1] == s[j + 1]) j++;
nex[i + 1] = j; // 为什么这里不是 nex[i + 1] = j + 1?因为 j 取次长时可能是因为不可能匹配(j = 0)跳出循环
}
return;
}
求出现位置与 \(next\) 数组。
代码:
// Problem: P3375 【模板】KMP
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3375
// Memory Limit: 512 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
/*+ Nimbunny +*/
#include <bits/stdc++.h>
#define endl '\n'
#define pi pair<int, int>
// #define int long long
// #pragma GCC optimize(2)
using namespace std;
const int INF = INT_MAX;
const int mod = 1e9 + 7;
const int N = 1e6 + 10;
string root, s;
int n, m, nex[N];
inline int read() {
int x;
cin >> x;
return x;
}
inline void init() {
nex[0] = nex[1] = 0;
for (int i = 1, j = 0; i < m; i++) {
while (j && s[i + 1] != s[j + 1]) j = nex[j];
if (s[i + 1] == s[j + 1]) j++;
nex[i + 1] = j;
}
return;
}
signed main() {
cin.tie(nullptr)->sync_with_stdio(false);
cin >> root >> s;
n = root.size(), m = s.size();
root = "#" + root, s = "#" + s;
init();
for (int l = 0, r = 0; l < n; l++) {
while (r && root[l + 1] != s[r + 1]) r = nex[r];
if (root[l + 1] == s[r + 1]) r++;
if (r == m)
cout << l + 1 - m + 1 << endl;
}
for (int i = 1; i <= m; i++) cout << nex[i] << " ";
return 0;
}
1.3.3 时间复杂度
为了更直观地理解为什么 KMP 是线性的,可以分开这样想:
-
next数组构造:在构造
next数组时,\(i\) 和 \(j\) 指针都只能向前移动(\(i\) 和 \(j\) 同时增加)或 \(j\) 向后跳(\(j=next_{j}\))。每次 \(j\) 向后跳都对应于之前的前进,因此 \(j\) 的“后退”总次数不会超过“前进”的总次数。因此,整个过程是线性的。 -
匹配过程:类似地,在匹配过程中,\(i\) 和 \(j\) 同时前进,或者 \(j\) 根据
next数组后退。每次后退都对应于之前的前进,因此总的操作次数与文本和模式的总长度成正比。
举个例子:
假设 \(root =\) ababaca,\(S =\) abababacaba。
构造next数组:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| P | a | b | a | b | a | c | a | |
| next | -1 | 0 | 0 | 1 | 2 | 3 | 0 | 1 |
构造过程中,i和j的变化如下:
- i=0, j=-1: next[0]=-1, i++, j++ → i=1, j=0
- i=1, j=0: root[1]=b != root[0]=a → j=next[0]=-1
- i=1, j=-1: next[1]=0, i++, j++ → i=2, j=0
- i=2, j=0: root[2]=a == root[0]=a → next[2]=1, i++, j++ → i=3, j=1
- i=3, j=1: root[3]=b == root[1]=b → next[3]=2, i++, j++ → i=4, j=2
- i=4, j=2: root[4]=a == root[2]=a → next[4]=3, i++, j++ → i=5, j=3
- i=5, j=3: root[5]=c != root[3]=b → j=next[3]=1
- i=5, j=1: root[5]=c != root[1]=b → j=next[1]=0
- i=5, j=0: root[5]=c != root[0]=a → j=next[0]=-1
- i=5, j=-1: next[5]=0, i++, j++ → i=6, j=0
- i=6, j=0: root[6]=a == root[0]=a → next[6]=1, i++, j++ → i=7, j=1
可以看到,虽然 \(j\) 有时会多次后退,但每次后退都对应于之前的前进,因此总的操作次数是线性的。
匹配过程:
类似地,在匹配过程中,\(i\) 和 \(j\) 的前进和后退也是成比例的,确保整个过程是线性的。
通过上述分析,我们可以严谨且直观地证明KMP算法的时间复杂度为 \(\mathcal{O}(n+m)\) ,其中 \(n\) 是文本的长度,\(m\) 是模式的长度。这得益于 \(next\) 数组的巧妙构造和匹配过程中指针的有效移动,避免了不必要的回溯。
1.4 例题
I. P2375 [NOI2014] 动物园
题意
给出 \(n\) 个字符串 \(S\),对于每个字符串求出它每个前缀的满足长度不超过 \(\frac{\mid S\mid}2\) 的 border 个数(即前后缀不重叠)。
\(1\le n\le5,1\le\mid S\mid\le10^6\)。
注意到对于一个字符串 border 的 border 也是原串的 border,所以通过不断跳 \(f\),我们能得到一个字符串的所有 border。
那么我们就能得到一个朴素的做法,即不断跳,然后记录个数。
但这显然是不对的,一个字符串的 border 有 \(\mathcal{O}(n)\) 级别,遍历完所有的就是平方的复杂度。
不过没关系,注意到 border 一定是原串的一个前缀,我们直接对于每个前缀记录一下它有多少个 border 即可。求的时候可以很简单的递推,即:\(g_i=g_{f_i}+1\)。
不难发现,根据 border 关系,这些前缀构成了一棵树,称为 fail 树,上述我们求的东西就是每个点的深度。
// Problem: P2375 [NOI2014] 动物园
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2375
// Memory Limit: 512 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
/*
author: Nimbunny
powered by c++14
*/
#include <bits/stdc++.h>
#define endl '\n'
#define pi pair<int, int>
#define int long long
using namespace std;
const int INF = INT_MAX;
const int mod = 1e9 + 7;
const int N = 1e6 + 10;
int n, ans;
string s;
inline int read() {
int x;
cin >> x;
return x;
}
struct KMP {
int nxt[N], num[N];
inline void getnext() {
for (int i = 2, j = 0; i <= n; i++) {
while (j && s[i] != s[j + 1]) j = nxt[j];
if (s[i] == s[j + 1]) j++;
nxt[i] = j;
num[i] = num[j] + 1;
}
return;
}
inline void getnum() {
for (int i = 2, j = 0; i <= n; i++) {
while (j && s[i] != s[j + 1]) j = nxt[j];
if (s[i] == s[j + 1]) j++;
while (j > (i >> 1)) j = nxt[j];
ans = (ans * (num[j] + 1)) % mod;
}
return;
}
} S;
inline void solve() {
ans = 1;
S.num[1] = 1;
cin >> s;
n = s.size();
s = "#" + s;
S.getnext(), S.getnum();
cout << ans << endl;
return;
}
signed main() {
cin.tie(nullptr)->sync_with_stdio(false);
int _ = read();
while (_--) solve();
return 0;
}
*II. P5829 【模板】失配树
这题是一道很好的深度理解 KMP 的题目。
问题是求 \(a_{1\dots p}\) 和 \(a_{1\dots q}\) 的最长公共 border 的长度。
先对原字符串做一次 KMP,于是我们可以通过跳两个前缀的 \(next\) 求两个前缀的所有 border。
注意,下面这个思路很重要:
通过 \(next\) 数组建一棵树,将 \(next_i\to i\),这样,我们把一个字符串转化到树上,是一棵有根树,叫失配树。我们可以在树上进行各种操作(树剖,倍增,动态树等),这种树我们叫做 fail 树。
P5829
// Problem: P5829 【模板】失配树
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5829
// Memory Limit: 512 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
/*
author: Nimbunny
powered by c++14
*/
#include <bits/stdc++.h>
#define endl '\n'
#define pi pair<int, int>
using namespace std;
const int INF = INT_MAX;
const int mod = 1e9 + 7;
const int N = 1e6 + 10, L = 20;
int n;
string s;
inline int read() {
int x;
cin >> x;
return x;
}
struct fail_tree {
int fa[N][L], dep[N];
inline void init() {
for (int i = 1; i < L; i++)
for (int j = 1; j <= n; j++)
fa[j][i] = fa[fa[j][i - 1]][i - 1];
return;
}
inline int lca(int u, int v) {
if (dep[u] < dep[v]) swap(u, v);
for (int i = L - 1; i >= 0; i--)
if (dep[fa[u][i]] >= dep[v]) u = fa[u][i];
for (int i = L - 1; i >= 0; i--)
if (fa[u][i] != fa[v][i]) u = fa[u][i], v = fa[v][i];
return fa[u][0];
}
} T;
signed main() {
cin >> s;
n = s.size();
s = "#" + s;
T.dep[1] = 1;
for (int i = 2, j = 0; i <= n; i++) {
while (j != 0 && s[j + 1] != s[i]) j = T.fa[j][0];
if (s[j + 1] == s[i]) j++;
T.fa[i][0] = j;
T.dep[i] = T.dep[j] + 1;
}
T.init();
int m = read();
while (m--) {
int x = read(), y = read();
cout << T.lca(x, y) << endl;
}
return 0;
}
III. P3435 [POI 2006] OKR-Periods of Words
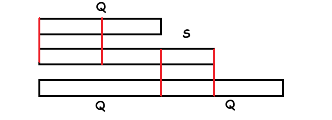
不难发现,红色框部分对应了 \(S\) 的一个 border。所以我们要求最长的 \(Q\),实际上就是要求最小的 border。
在 fail 树上不断向上跳,并且跳的时候做一个记忆化即可。
P3435
// Problem: P3435 [POI 2006] OKR-Periods of Words
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3435
// Memory Limit: 128 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
/*
author: Nimbunny
powered by c++14
*/
#include <bits/stdc++.h>
#define endl '\n'
#define ull unsigned long long
#define pi pair<int, int>
using namespace std;
const int INF = INT_MAX;
const int mod = 1e9 + 7;
const int N = 1e6 + 10;
int n, nex[N];
ull ans;
string s;
signed main() {
cin.tie(nullptr)->sync_with_stdio(false);
cin >> n >> s;
s = "#" + s;
for (int i = 2, j = 0; i <= n; i++) {
while (j && s[i] != s[j + 1]) j = nex[j];
if (s[i] == s[j + 1]) j++;
nex[i] = j;
}
for (int i = 2, j = 2; i <= n; i++, j = i) {
while (nex[j]) j = nex[j];
if (nex[i]) nex[i] = j;
ans += i - j;
}
cout << ans << endl;
return 0;
}
IV. P3546 [POI 2012] PRE-Prefixuffix
题意
对于两个串 \(S_1,S_2\),如果能够将 \(S_1\) 的一个后缀移动到开头后变成 \(S_2\),就称 \(S_1\) 和 \(S_2\) 循环相同。例如串 ababba 和串 abbaab 是循环相同的。
给出一个长度为 \(n\) 的串 \(S\),求满足下面条件的最大的 \(L(L\le \frac{n}2)\):\(S\) 的 \(L\) 前缀和 \(S\) 的 \(L\) 后缀是循环相同的。
\(1\le n\le10^6\)。
注意到两个字符串 \(s_1,s_2\) 是循环相等,当且仅当存在两个字符串 \(A,B\),使得 \(s_1=A+B,s_2=B+A\),其中 \(+\) 表示字符串拼接。
进一步转化可以发现,实际上是在原字符串两边删掉一个 border 后,求剩下的字符串的最长不重叠 border。
相当于求出原字符串的 ABSBA 的表示形式。A...A 可以用 kmp 枚举,但是中间的 \(B\) 无法处理。
注意到两个字符串 \(s_1,s_2\) 是循环相等,当且仅当存在两个字符串 \(A,B\),使得 \(s_1=A+B,s_2=B+A\),其中 \(+\) 表示字符串拼接。
进一步转化可以发现,实际上是在原字符串两边删掉一个 border 后,求剩下的字符串的最长不重叠 border。
相当于求出原字符串的 ABSBA 的表示形式。A...A 可以用 kmp 枚举,但是中间的 \(B\) 无法处理。
但我们发现如果设 \(f_i\) 表示去掉长度为 \(i\) 的前后缀后的字符串的 border,则应该有:
所以可以 \(+2\) 后暴力判断,可以用哈希判断是否相等。
P3546
// Problem: P3546 [POI 2012] PRE-Prefixuffix
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3546
// Memory Limit: 64 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
/*
author: Nimbunny
powered by c++14
*/
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
#define pi pair<int, int>
using namespace std;
const int INF = INT_MAX;
const int mod = 1e9 + 7;
const int N = 1e6 + 5, P = 1331;
int n, ans, f[N], nex[N], hsh[N], pw[N];
string s;
inline int calc(int l, int r) {
l--;
return (hsh[r] - hsh[l] * pw[r - l] % mod + mod) % mod;
}
signed main() {
cin.tie(nullptr)->sync_with_stdio(false);
cin >> n >> s;
s = "#" + s;
pw[0] = 1;
for (int i = 1; i <= n; i++) pw[i] = pw[i - 1] * P % mod;
for (int i = 2, j = 0; i <= n; i++) {
while (j && s[j + 1] != s[i]) j = nex[j];
j += (s[j + 1] == s[i]);
nex[i] = j;
}
for (int i = 1; i <= n; i++)
hsh[i] = (hsh[i - 1] * P + s[i]) % mod;
for (int i = n >> 1; i; i--) {
f[i] = f[i + 1] + 2;
while (f[i]) {
if ((i + f[i]) * 2 > n)
f[i]--;
else if (calc(i + 1, i + f[i]) !=
calc(n - i - f[i] + 1, n - i))
f[i]--;
else
break;
}
}
for (int i = nex[n]; i; i = nex[i])
if (i * 2 <= n) ans = max(ans, f[i] + i);
cout << ans << endl;
return 0;
}
2. Manacher
问题陈述:
给定一个字符串 \(s\),求出最长的 \(s\) 的子串,使得这个子串和其反串相同(即回文串)。
2.1 概念
Manacher 算法是一种用于求解单串回文结构的算法。
具体的,对于 \(s\) 中的每个位置 \(i\),Manacher 算法可以求出以位置 \(i\) 为中心的最长回文串的半径长度。
得到这个信息,对于处理回文串问题有非常大帮助。
2.2 算法流程
为了减少讨论,我们通常先在 \(s\) 的开头和结尾各补一个不同的罕见字符。
先考虑计算所有奇数长度回文子串。记 \(p_i\) 表示以位置 \(i\) 为中心的最长回文半径长度,我们仍然考虑用 \(p_1,···,p_{i−1}\) 递推 \(p_i\)。
定义 \(mr\) 表示之前的 \(i+p_i−1\) 的最大值 (即最靠右的回文串)。同时记录这个回文中心为 \(mid\) (如果有多个,记录最靠右的)。
考虑当前位置 \(i\):
- 如果 \(i\le mr\),则设置初值为 \(p_i=\min(p_{mid\times 2−i},mr−i+1)\)。
- 否则设置初值为 \(p_i=1\)。
- 之后暴力向两侧扩展 \(p_i\),并更新 \(mid\) 和 \(mr\)。

时间复杂度:
空间复杂度显然为 \(\mathcal{O}(\mid s\mid)\)。
算法复杂度瓶颈在于暴力扩展部分的复杂度。
对于 \(i\le mr\) 的情况,当 \(p_{mid\times2−i}<mr−i+1\) 时,不会做暴力扩展。
注意到每次做暴力扩展时,都会让 \(mr\) 至少增加 \(1\)。
整个算法运行过程中,\(mr\) 不减,且上界为 \(\mid s\mid\)。
所以 Manacher 算法的时间复杂度为 \(\mathcal{O}(\mid s\mid)\)。
2.3 完整算法
上述算法只能处理奇数长度回文子串,如何处理偶数长度?
将 \(s\) 的相邻两个字符之间添一个相同的罕见字符即可,注意这里的 \(s\) 是上述算法特殊处理过的 \(s\)。
需要注意现在处理出来的回文半径是原来的 \(2\) 倍 \(\pm1\),要根据奇偶性讨论一下。
代码:
inline void build() {
scanf("%s", c + 1);
n = strlen(c + 1);
s[++cnt] = '~', s[++cnt] = '#';
for (int i = 1; i <= n; i++) {
s[++cnt] = c[i];
s[++cnt] = '#';
}
s[++cnt] = '!';
return;
}
inline void solve() {
for (int i = 2; i < cnt; i++) {
if (i <= mr)
p[i] = min(p[mid * 2 - i], mr - i + 1);
else
p[i] = 1;
while (s[i - p[i]] == s[i + p[i]]) p[i]++;
if (i + p[i] > mr) mr = i + p[i] - 1, mid = i;
ans = max(ans, p[i]);
}
printf("%d", ans - 1);
return;
}
2.4 例题
I. UVA11475 Extend to Palindrome
题意
给出一个字符串 \(S\),求出一个字符串 \(S∗\),满足:
- \(S\) 是 \(S∗\) 的前缀;
- \(S∗\) 是一个回文串;
- \(\mid S∗\mid\) 最小化;
\(\mid S\mid\le10^5\)。
利用 Manacher 处理出最长回文半径后,找到最长回文后缀即可。
构造 \(S∗\) 直接把删除最长后缀的 \(S\) 反过来拼在 \(S\) 后面即可。
时间复杂度 \(\mathcal{O}(\mid S\mid)\)。
UVA11475
// Problem: UVA11475 Extend to Palindrome
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/UVA11475
// Memory Limit: 0 MB
// Time Limit: 3000 ms
//
// Powered by CP Editor (https://cpeditor.org)
/*
author: Nimbunny
powered by c++14
*/
#include <bits/stdc++.h>
#define endl '\n'
#define pi pair<int, int>
#define int long long
// #pragma GCC optimize(2)
using namespace std;
const int INF = INT_MAX;
const int mod = 1e9 + 7;
const int N = 5e5 + 10;
int len, n, d[N];
string a;
char s[N];
signed main() {
cin.tie(nullptr)->sync_with_stdio(false);
while (cin >> a) {
memset(d, 0, sizeof d);
d[0] = 1;
len = a.size();
n = 0;
s[0] = '#';
for (int i = 0; i < len; i++) {
s[++n] = a[i];
s[++n] = '#';
}
int l = 0, r = -1;
for (int i = 1; i <= n; i++) {
if (i > r)
while (0 <= i - d[i] && i + d[i] <= n &&
s[i - d[i]] == s[i + d[i]])
d[i]++;
else {
int j = l + r - i;
if (j - d[j] + 1 <= l) {
d[i] = r - i;
while (0 <= i - d[i] && i + d[i] <= n &&
s[i - d[i]] == s[i + d[i]])
d[i]++;
} else
d[i] = d[j];
}
l = i - d[i] + 1;
r = i + d[i] - 1;
if (r == n) break;
}
for (int i = 1; i < l; i++)
if (s[i] != '#') cout << s[i];
for (int i = l; i <= r; i++)
if (s[i] != '#') cout << s[i];
for (int i = l - 1; i >= 1; i--)
if (s[i] != '#') cout << s[i];
cout << endl;
}
return 0;
}
II. P4555 [国家集训队] 最长双回文串
题意
给出一个字符串 \(S\)。定义 \(s\) 双回文串当且仅当 \(s\) 可以被拆为 \(x+y\) 并且 \(x\) 和 \(y\) 都是回文串。
求出 \(S\) 的最长双回文子串的长度。
\(\mid S\mid\le10^5\)。
我们可以处理出每个位置 \(i\):以 \(i\) 开头的最长回文子串 \(l_i\) 和以 \(i\) 结尾的最长回文子串 \(r_i\)。答案就是 \(r_i+l_{i+1}\) 的最大值。
用 Manacher 求出最长回文半径,我们可以先给最长的回文串(\([i−p[i]+1,i+p[i]−1]\))打上标记,之后可以向内每次减少 \(2\) 递推。
或者选择在每次 manacher 暴力扩展 \(mr\) 的时候顺便更新,因为第一个碰到后面的 \(i\) 一定是最小的 \(i\),对应最大的回文半径。
时间复杂度 \(\mathcal{O}(\mid S\mid)\)。
P4555
// Problem: P4555 [国家集训队] 最长双回文串
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4555
// Memory Limit: 125 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
/*
author: Nimbunny
powered by c++14
*/
#include <bits/stdc++.h>
#define endl '\n'
#define pi pair<int, int>
#define int long long
// #pragma GCC optimize(2)
using namespace std;
const int INF = INT_MAX;
const int mod = 1e9 + 7;
const int N = 100010 << 1;
int n, p[N], pos[N][2], ans;
char s[N];
inline void read() {
s[0] = '~';
s[n = 1] = '|';
char c = getchar();
while (c < 'a' || c > 'z') c = getchar();
while (c >= 'a' && c <= 'z') {
s[++n] = c;
s[++n] = '|';
c = getchar();
}
return;
}
signed main() {
cin.tie(nullptr)->sync_with_stdio(false);
read();
for (int i = 1, mid = 0, r = 0; i <= n; i++) {
if (i <= r) p[i] = min(p[(mid << 1) - i], r - i + 1);
while (s[i - p[i]] == s[i + p[i]]) p[i]++;
if (i + p[i] - 1 > r) {
r = i + p[i] - 1;
mid = i;
}
pos[i + p[i] - 1][0] = max(pos[i + p[i] - 1][0], p[i] - 1);
pos[i - p[i] + 1][1] = max(pos[i - p[i] + 1][1], p[i] - 1);
}
for (int i = 3; i <= n; i += 2)
pos[i][1] = max(pos[i][1], pos[i - 2][1] - 2);
for (int i = n; i >= 3; i -= 2)
pos[i][0] = max(pos[i][0], pos[i + 2][0] - 2);
for (int i = 3; i <= n; i += 2)
if (pos[i][0] && pos[i][1])
ans = max(ans, pos[i][0] + pos[i][1]);
cout << ans << endl;
return 0;
}
III. P5446 [THUPC 2018] 绿绿和串串
题意
给出一个字符串 \(\mid S\mid\)。定义对 \(R\) 进行一次翻转操作位将 \(R[1,\mid R\mid−1]\) 反过来拼在 \(R\) 后面。
求所有可能的 \(\mid R\mid\),使得 \(R\) 经过若干次翻转后其前缀为 \(S\)。
\(\mid S\mid\le5\times10^6\)。
如果位置 \(i\) 的最大回文半径足够达到 \(S\) 的结尾 \((i+p_i−1=\mid S\mid)\),则 \(i\) 是一个可行答案,给 \(i\) 打上标记。
如果位置 \(i\) 的最大回文半径足够达到 \(S\) 的开头 \((i−p_i+1=1)\),并且 \(i+p_i−1\) 被标记过,那么 \(i\) 也是一个可行答案,也打上标记。
不难发现只有这两种情况合法,倒推即可。
时间复杂度为 \(\mathcal{O}(\mid S\mid)\)。
P5446
// Problem: P5446 [THUPC 2018] 绿绿和串串
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5446
// Memory Limit: 500 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
/*
author: Nimbunny
powered by c++14
*/
#include <bits/stdc++.h>
#define endl '\n'
#define pi pair<int, int>
// #define int long long
using namespace std;
const int INF = INT_MAX;
const int mod = 1e9 + 7;
const int N = 2e6 + 10;
int n, d[N], ans[N], vis[N], tp;
string s;
inline void manacher(string s, int n) {
memset(d, 0, sizeof d);
for (int i = 1, l = 1, r = 0; i <= n; i++) {
int k = i > r ? 1 : min(d[l + r - i], r - i + 1);
while (i - k >= 1 && i + k <= n && s[i - k] == s[i + k]) k++;
d[i] = k--;
if (i + k > r) {
r = i + k;
l = i - k;
}
}
return;
}
inline void dfs(int x, int tag) {
ans[++tp] = x;
vis[x] = tag;
int pos = x / 2 + (x & 1);
if (pos + d[pos] - 1 >= x)
if (vis[pos] != tag) dfs(pos, tag);
return;
}
inline int read() {
int x;
cin >> x;
return x;
}
signed main() {
cin.tie(nullptr)->sync_with_stdio(false);
int T = read() + 1;
while (--T) {
cin >> s;
n = s.size();
s = "#" + s;
manacher(s, n);
for (int j = n; j >= 1; j--) {
if (vis[j] == T) break;
if (j + d[j] <= n) continue;
dfs(j, T);
}
sort(ans + 1, ans + tp + 1);
for (int i = 1; i <= tp; i++) cout << ans[i] << " ";
cout << endl;
tp = 0;
}
return 0;
}
IV. P6216 回文匹配
题意
给出两个字符串 \(s_1,s_2\),求 \(s_2\) 在 \(s_1\) 所有奇数长度回文串中出现次数之和。
\(\mid s_1\mid,\mid s_2\mid\le3\times10^6\)。
预处理 \(t\) 在 \(s\) 中的所有匹配位置并标记,这个可以用 KMP 解决。
朴素的做即为枚举每个回文串,累加区间内标记数量 (注意需要考虑 \(t\) 要完整出现在区间内)。
求出回文半径后,问题变为了类似求等差数列的结果,形如 \(\displaystyle\sum_{i=l}^{r}tag_i\times(i−l+1)\)。
直接拆贡献,变为 \(\sum^r_{i=l}tag_i\times i+\sum^r_{i=l}tag_i\times(1−l)\),利用前缀和即可解决。
时间复杂度 \(\mathcal{O}(\mid s_1\mid+\mid s_2\mid)\)。
P6216
// Problem: P6216 回文匹配
// Contest: luogu
// Url: https://www.luogu.com.cn/problem/P6216
// Memory limit: 512 MB
// Time limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
/*
author: Nimbunny
powered by c++14
*/
#include <bits/stdc++.h>
#define endl '\n'
#define pi pair<int, int>
#define int long long
// #pragma GCC optimize(2)
using namespace std;
const int INF = 0x3f3f3f3f;
const int mod = 4294967296;
const int N = 3e6 + 10;
int n, len[N << 1];
int fail[N], len1, len2, sum[N];
string s1, s2;
char s[N << 1];
inline int read() {
int x;
cin >> x;
return x;
}
inline void kmp() {
fail[1] = 0;
for (int j, i = 2; i <= len2; i++) {
j = fail[i - 1];
while (j && s2[j + 1] != s2[i]) j = fail[j];
if (j)
fail[i] = j + 1;
else
fail[i] = (s2[1] == s2[i]);
}
for (int j = 0, i = 1; i <= len1; i++) {
while (s1[i] != s2[j + 1] && j) j = fail[j];
if (s1[i] == s2[j + 1]) j++;
if (j == len2) {
j = fail[j];
sum[i - len2 + 1] = 1;
}
}
return;
}
inline int manacher() {
int ans = 0;
s[0] = 1, s[1] = 2;
n = 1;
for (int i = 1; i <= len1; i++) s[++n] = s1[i], s[++n] = 2;
s[n + 1] = 3;
int pos = 0, ma = 0;
for (int i = 1, l, r; i <= n; i++) {
if (pos + ma - 1 < i)
len[i] = 1;
else
len[i] = min(len[pos * 2 - i], pos + ma - i);
while (s[i + len[i]] == s[i - len[i]]) len[i]++;
if (i + len[i] - 1 >= pos + ma - 1) {
pos = i;
ma = len[i];
}
l = (i - len[i] + 2) >> 1;
r = ((i + len[i] - 2) >> 1) - len2 + 1;
if (s[i] != 2 && r >= l) {
ans += sum[r] - sum[r - ((r - l) >> 1) - 1] -
sum[l + ((r - l) >> 1) - 1] + sum[max(l - 2, 0ll)];
ans %= mod;
}
}
return ans % mod;
}
signed main() {
cin.tie(nullptr)->sync_with_stdio(false);
len1 = read(), len2 = read();
cin >> s1 >> s2;
s1 = "#" + s1, s2 = "#" + s2;
if (len1 < len2) return cout << 0 << endl, 0;
kmp();
for (int i = 1; i <= len1; i++) sum[i] += sum[i - 1];
for (int i = 1; i <= len1; i++) sum[i] += sum[i - 1];
cout << manacher() << endl;
return 0;
}
3. Z Algorithm
Z Algorithm 就是 exKMP。
3.1 回顾:双串模式匹配
问题陈述:
给定一个模式串 \(s\) 和一个文本串 \(t\),查询这个模式串是否在文本串里出现过。
双串模式匹配我们可以使用 KMP 算法解决。回顾 KMP 算法的核心思想是预处理出每个前缀的 border。
3.2 加强的问题
问题描述
给出一个长度为 \(n\) 的字符串 \(s\),求出每个后缀和这个串本身的最长公共前缀 (LCP) 的长度。
例:\(z(”aaabaab”)=[7,2,1,0,2,1,0]\)。
定义函数 \(z_i\) 表示 \(s\) 和 \(s[i,n]\) (即以 \(s_i\) 开头的后缀) 的 LCP 长度。
求解 \(z\) 函数的算法称为 Z Algorithm,也叫 exKMP (但实际和 KMP 没什么联系)。
3.3 算法流程
在该算法中,我们从 \(2\) 到 \(n\) 顺次计算 \(z_i\) 的值 \((z_0=0,z_1=n)\)。我们利用已经计算好的 \(z_1,\dots,z_{i−1}\) 来递推出 \(z_i\)。
对于 \(i\),我们称区间 \([i,i+z_i−1]\) 是 \(i\) 的匹配段,也叫做 Z-box。
算法的过程中我们维护右端点最靠右的匹配段,记作 \([l,r]\)。根据定义,\(s[l,r]\) 是 \(s\) 的前缀。在计算 \(z_i\) 时我们保证 \(l\le i\)。初始时 \(l=r=0\)。
在计算 \(z_i\) 的过程中:
-
如果 \(i\le r\),根据定义有 \(s[i,r]=s[i−l+1,r−l+1]\),因此 \(z_i\ge min(z_{i−l+1},r−i+1)\)。此时:
- 若 \(z_{i−l+1}<r−i+1\),则 \(z_i=z_{i−l+1}\)。
- 否则 \(z_{i−l+1}\ge−i+1\),这是我们令 \(z_i=r−i+1\),然后暴力枚举下一个字符扩展 \(z_i\),直到不能扩展为止。
-
如果 \(i>r\),直接暴力求出 \(z_i\)。
-
在求出 \(z_i\) 后,如果 \(i+z_i−1>r\),则更新 \(l=i,r=i+z_i−1\)。
代码:
inline void Z(char *s, int n) {
for (int i = 1; i <= n; i++) z[i] = 0;
z[1] = n;
for (int i = 2, l = 0, r = 0; i <= n; i++) {
if (i <= r) z[i] = min(z[i - l + 1], r - i + 1);
while (i + z[i] <= n && s[i + z[i]] == s[z[i] + 1]) z[i]++;
if (i + z[i] - 1 > r) l = i, r = i + z[i] - 1;
}
}
复杂度分析:
空间复杂度显然是 \(\mathcal{O}(n)\)。
对于内层循环,每次执行都会使得 \(r\) 向后至少移 \(1\) 位,而 \(r<n−1\),所以总共只会执行 \(n\) 次。
对于外层循环,只有一遍线性遍历。
所以总时间复杂度为 \(\mathcal{O}(n)\)。
3.4 两个串的 p 函数
定义两个串 \(s\) 关于 \(t\) 的 p 函数为:\(p_i\) 等于 \(t\) 与 \(s\) 的每个后缀的 LCP 长度。
我们先求出 \(t\) 的 \(z\) 函数,再递推 p 函数:
- 如果 i ≤ r,根据定义有 \(s_{i,r}=t_{i−l+1,r−l+1}\),因此 \(p_i\ge\min(z_{i−l+1},r−i+1)\)。此时:
- 若 \(z_{i−l+1}<r−i+1\),则 \(p_i=z_{i−l+1}\)。
- 否则 \(z_{i−l+1}\ge r−i+1\),这是我们令 \(p_i=r−i+1\),然后暴力枚举下一个字符扩展 \(z_i\),直到不能扩展为止。
- 如果 \(i>r\),直接暴力求出 \(p_i\)。
- 在求出 \(p_i\) 后,如果 \(i+p_i−1>r\),则更新 \(l=i,r=i+p_i−1\)。
代码:
inline void exkmp(char *s, int n, char *t, int m) {
Z(t, m);
for (int i = 1; i <= n; i++) p[i] = 0;
for (int i = 1, l = 0, r = 0; i <= n; i++) {
if (i <= r) p[i] = min(z[i - l + 1], r - i + 1);
while (i + p[i] <= n && s[i + p[i]] == t[p[i] + 1]) p[i]++;
if (i + p[i] - 1 > r) l = i, r = i + p[i] - 1;
}
return;
}
3.5 例题
I. P7114 [NOIP2020] 字符串匹配
题意
给出一个字符串 \(S(\mid S\mid\le2^{20})\)。定义一个合法的拆分为 \(S=(AB)^kC,k\ge1\),三个字符串都非空,并且 \(F(A)\le F(C)\),\(F(s)\) 表示字符串 \(s\) 中出现奇数次的字符数量。
两个方案被认为不同当且仅当 \(A,B,C\) 中至少有一个字符串不同,求合法的拆分的方案数。
先忽略 \(F(A)\le F(C)\) 的限制。
不妨枚举 \(D=AB\) 的长度。当 \(D\) 长为 \(x\) 时,不难发现 \(k\) 的取值范围是 \([1,\lfloor\frac{z_{x+1}}x\rfloor]\)。
用 exkmp 算法即可解决这个弱化问题。
再加上 \(F(A)≤F(C)\) 的限制。记 \(f(l,r)\) 表示 \(s[l,r]\) 中出现奇数次的字符的个数。
当 \(k\) 为奇数时,容易发现都和 \(k=1\) 的情况相同,于是只需要计算 \(f(1,j)≤f(x+1,n),j\le x−1\) 的 \(j\) 的数量,与 \(\lceil\frac{\lfloor\frac{z_{x+1}}x\rfloor}2\rceil\) 相乘累加进答案。
当 \(k\) 为偶数时,容易发现都和 \(k=2\) 的情况相同,于是只需要计算 \(f(1,j)\le f(2x+1,n),j\le x−1\) 的 \(j\) 的数量,与 \(\lfloor\frac{\lfloor\frac{z_{x+1}}x\rfloor}2\rfloor\) 相乘累加进答案。
现在只需要能支持快速查询 \(f(1,x)\) 和 \(f(x,n)\),后者可以预处理,前者要查询小于等于某个值的数量。
因为 \(f(1,x)\) 的取值只有 \(26\) 种,可以直接用树状数组维护,足够通过。
时间复杂度为 \(\mathcal{O}(\mid s\mid\log26)\)。
P7114
II. CF432D Prefixes and Suffixes
题意
给出一个字符串 \(s\),定义完美前缀为:这个前缀同时是 \(s\) 的后缀。
求出完美前缀的个数和分别的在 \(s\) 中的出现次数。
\(\mid s\mid\le10^5\)。
构造字符串 \(t=s+'|'+s\),求出 \(t\) 的 z 函数。
枚举 \(t\) 的后半部分,容易发现 \(s_{1,i}\) 是一个完美前缀当且仅当 \(z_{\mid s\mid+1+\mid s\mid−i+1}=i\)。
求完美前缀 \(s_{1,i}\) 的出现次数即为求后半部分的 z 函数中有多少个位置满足 \(z_{\mid s\mid+1+x}\ge x\),开个桶求后缀和即可。
时间复杂度为 \(\mathcal{O}(\mid s\mid)\)。
CF432D
III. CodeChef Chef and String
题意
给出一个字符串 \(s\),记所有 \(s\) 的非空子串组成的集合为 \(L\)。
\(q\) 次询问,求出从 \(L\) 中选出 \(k_i\) 个相同字符串的方案数,对大质数取模。
\(n\le5000,q\le105,k\le10^9\)。
先考虑求出所有本质不同的子串。考虑计算增量,即在知道当前 \(s\) 的本质不同子串数的情况下,计算出在 \(s\) 末尾添加一个字符后的本质不同子串数。
设串 \(t\) 是 \(s+c\) 的反串(反串指将原字符串的字符倒序排列形成的字符串)。我们的任务是计算有多少 \(t\) 的前缀未在 \(t\) 的其他地方出现。考虑计算 \(t\) 的 z 函数并找到其最大值 \(z_{max}\)。则 \(t\) 的长度小于等于 \(z_{max}\) 的前缀的反串在 \(s\) 中是已经出现过的以 \(c\) 结尾的子串。
于是新增的本质不同的子串为 \(s+c,\dots,s[\mid s\mid+1−z_{max},\mid s\mid]+c\)。
这部分复杂度为 \(\mathcal{O}(n^2)\)。
再考虑每个子串的出现次数。
我们把左端点相同的子串放一起考虑,假设左端点都为 \(l\),我们先求出 \(s[l,\mid s\mid]\) 的 z 函数。
对于 \(s[l,r]\),其出现次数即为 \(z_j>=r−l+1,j>l\) 的 \(j\) 的数量。
于是用一个桶和后缀和即可统计。
这部分复杂度为 \(\mathcal{O}(n^2)\)。
容易发现每个子串出现次数不会超过 \(n\),于是可以 \(\mathcal{O}(n^2)\) 预处理,\(\mathcal{O}(1)\) 回答。
总复杂度为 \(\mathcal{O}(n^2+q)\)。
CodeChef CHSTR
// Problem: Chef and String
// Contest: CodeChef - JUNE15
// URL: https://www.codechef.com/problems/CHSTR
// Memory Limit: 256 MB
// Time Limit: 1500 ms
//
// Powered by CP Editor (https://cpeditor.org)
/*
author: Nimbunny
powered by c++14
*/
#include <bits/stdc++.h>
#define endl '\n'
#define pi pair<int, int>
#define int long long
// #pragma GCC optimize(2)
using namespace std;
const int INF = INT_MAX;
const int mod = 1e9 + 7;
const int N = 5e3 + 10;
int n, q, ans[N], k[N], c[N][N], vis[N], z[N];
string str;
inline void calc(string s) {
int n = s.size();
for (int i = 1, l = 0, r = 0; i < n; i++) {
if (i <= r && z[i - l] < r - i + 1)
z[i] = z[i - l];
else {
z[i] = max(0ll, r - i + 1);
while (z[i] < n && s[i + z[i]] == s[z[i]]) z[i]++;
}
if (i + z[i] - 1 > r) {
l = i;
r = i + z[i] - 1;
}
if (vis[n - i] < z[i]) {
k[z[i]]++;
vis[n - i] = z[i];
}
}
return;
}
inline int read() {
int x;
cin >> x;
return x;
}
inline void solve() {
memset(ans, 0, sizeof ans);
memset(vis, 0, sizeof vis);
n = read(), q = read();
cin >> str;
for (int i = n; i >= 1; i--) {
memset(k, 0, sizeof k);
string s = str.substr(0, i);
reverse(s.begin(), s.end());
calc(s);
k[i] = 1;
for (int p = i; p > vis[i]; p--) {
k[p] += k[p + 1];
for (int j = 1; j <= k[p]; j++)
if (k[p] >= j) ans[j] = (ans[j] + c[k[p]][j]) % mod;
}
}
for (int i = 1; i <= q; i++) {
int x = read();
cout << (x <= n ? ans[x] : 0) << endl;
}
return;
}
signed main() {
cin.tie(nullptr)->sync_with_stdio(false);
for (int i = 0; i <= 5000; i++) c[i][0] = 1;
for (int i = 1; i <= 5000; i++)
for (int j = 1; j <= i; j++)
c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod;
int _ = read();
while (_--) solve();
return 0;
}
3.6 小结
z 函数是一个非常强大的工具,不仅可以完成 kmp 的工作 (处理前缀问题),还可以处理一些子串问题。
求 z 函数的算法可以启发我们对于增量构造算法的思考,这是一个很实用的解题思路。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号