【算法】ST表

参考资料

算法学习笔记：ST表 | OI学习笔记 ST表 | ST表详解

一、概念

ST 表基于倍增思想，主要用于查询区间最值，比如询问区间 l，r 的最大值。

二、实现

首先有一种暴力的思想，定义 \(dp_{[i][j]}\) 为区间 i，j 的最值，原数组为 \(a_{[i]}\)。

显然有\(dp_{[i][j]}=max/min(dp_{[i][j-1],a[j]})\)。

但很明显，这样的时间、空间复杂度均不优秀，我们想到了上一次运用倍增算法来优化 LCA 问题，那么可以用它来优化吗？

定义一个数组 \(dp_{[i][j]}\) 表示从第 i 个数开始往后 \(2^j\) 的最值。

注意这里 \(j\) 不是区间的右端点，而是表示区间长度的一个参数。

不难发现，\(dp_{[i][0]}=a_{[i]}\)，此时区间长为 1。

然后我们画一个简易的图：

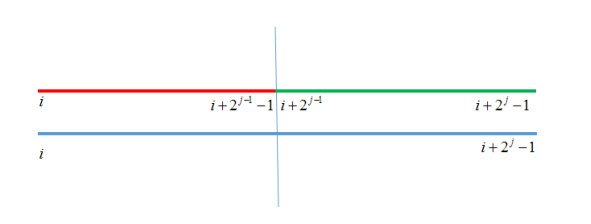
图片来源：OI学习笔记 ST表

从图中我们可以看出，这段区间的最大值也就等于红色段和绿色段的最大值，而两段的长都为\(2^{j-1}\)。

也就可以得出状态转移方程：

\[dp_{[i][j]}=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]) \]

查询时，我们可以针对左右两个端点，来分成两个区间。

由于我们希望能覆盖整个区间，于是可以考虑将第一个区间的右端点接近要查询的右端点，第二个区间的左端点接近要查询的左端点，所以我们可以分别向中间扩展 \(log_2\text(区间长度)\)，向下取正，然后查询，这样就一定能覆盖整个区间。在代码中体现为这样的：

点击查看代码

//l是查询区间左端点，r是查询区间右端点
int s=log2(r-l+1)
cout<<max(dp[l][s],dp[r-(1<<s)+1][r]);

这样一份最基础的 ST 表就完成了，如果依旧不懂可以看参考资料。

三、代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int dp[N][30];
int l[N];

int read() {
    int x=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-')f=0;c=getchar();}
    while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+c-48,c=getchar();}
    return f?x:-x;
}
int main(){
    int n=read(),m=read();
    for(int i=1;i<=n;i++) dp[i][0]=read();
    for(int i=2;i<=n;i++) l[i]=l[i>>1]+1;//预处理log
    for(int i=1;(1<<i)<=n;i++){//区间最长不能超过 n
	//当然这种也是可行的：for(int i=1;i<=log(n);i++)
        for(int j=1;j+(1<<i)-1<=n;j++){//区间的右端点不能超过 n
            dp[j][i]=max(dp[j][i-1],dp[j+(1<<(i-1))][i-1]);
        }
    }
    while(m--){
        int l=read(),r=read();
        int s=l[r-l+1];
        printf("%d\n", max(dp[l][s],dp[r-(1<<s)+1][s]));
    }
    return 0;
}

四、时间复杂度

操作	时间复杂度
初始化	O(n log n)
查询	O(1)

五、例题

咕