使用遗传算法和模拟退火算法解决八皇后问题

本文测试内容主要包括：

1）构建八皇后的类，类中包含有八皇后的属性矩阵、排列数组、评估函数数组等，以及实现各种基本功能的函数。

2）用模拟退火算法来解决八皇后问题，并测试什么样的参数和温度下降函数的求解效率比较高，分析模拟退火算法的优点和缺点。

3）设计遗传算法来解决八皇后问题，并测试什么样的参数的求解效率最高，分析遗传算法的优点与缺点。

先说结论，模拟退火算法和遗传算法都可以得到近似最优解，都收到参数设置的影响比较大，而模拟退火算法更可能找到最好的解，遗传算法可以得到最优解的近似解空间，该空间中有很多近似最优解。

本次使用的遗传算法是在传统算法的基础上做了一点点改进，改进内容如下：

种群中每个个体产生的时候由内部竞争产生：

​ 1.首先有交叉互换产生两个子代个体C1,C2

​ 2.如果没有发生交叉互换，则用亲本个体作为子代个体C1,C2

​ 3.分别对两个子代个体进行变异操作。

​ 4.选择C1、C2中适应值高的个体作为此次产生的个体。

​ 该改进将大幅减小找到全局解所需要的世代数，如果不这样做会产生很多子代才能有解。

更多的细节和详细的代码请访问我的github获取。

1.数据结构和基本操作

首先进行八皇后类的设计，接着完成针对八皇后问题的模拟退火算法的设计和遗传算法的设计。在类的设计中，要将八皇后封装起来，八皇后要设计属性：位置矩阵，并用一个一维数组来表示八个皇后的位置，最后再设计一个评估值矩阵，评估每个位置上可以被多少个皇后攻击的到。

我在这里设计了以下几个操作函数：

1.初始化方法：把棋盘清零，八个皇后都暂时不摆放。

2.根据排列方法来确定queen属性的值。内部先调用了一次 initial()，然后根据 state 数据成员往棋盘 board 放入 8 个皇后。

3.随机赋值排列函数。随机产生一个初始状态，赋值给 state 数据成员。

4.输出棋盘的函数。

5.输出棋盘评估函数值的函数。打印当前棋盘的 评估值函数 数据成员。

6.手动设置排列属性。手动设置初始状态 state 而不是随机产生

7.得到排列属性的函数。获得排列方式。

8.检查是否到了终止条件的函数。 检查当前棋盘上八皇后的放置是否已经满足要求，也即八皇后问题是否成功求解。

9.计算评估值的函数。启发式评估函数 —— 相互攻击的皇后的数量。

10.另一种计算评估值的函数。启发式评估函数 —— 不相互攻击的皇后的数量。

11.用于设置评估值属性的计算评估值的方法的函数。给定皇后的位置 x 和 y，该函数计算在棋盘 (x, y) 位置上的皇后与多少个其他位置上的皇后形成相互攻击 。

2.模拟退火算法解决八皇后问题

所谓退火，是为了达到某些特种晶体的结构重复把金属加热或冷却的过程了，该过程的控制参数为温度T。模拟退火算法的基本思想是：在系统朝着能量减小的趋势这样一个变化过程中，偶尔允许系统跳到能量较高的点，以避开局部最小点，最终稳定到全局最小点。这是我个人非常喜欢的一个算法。

模拟退火的步骤：

1.初始化温度和操作步数。

2.循环，随机改变某一皇后的位置，并依据评估函数和概率来决定是否选择改变皇后位置，更新温度：T=0.99*T;终止条件：T > 0.00001。

3.遗传算法解决八皇后问题

基本思想：使用模拟生物和人类进化的方法求解复杂的优化问题，因而也称为模拟进化优化算法。

遗传算法将择优与随机信息交换结合在一起，在每一代中，使用上代中最好的，即最适应环境的位或片段，形成新的人工生物集。

遗传算法是一个迭代过程，在每次迭代中都保留一组候选解，并按某种优劣指标进行排序，然后按某种指标从中选出一些解，利用遗传算子，即下面要讲到的遗传操作，对其进行运算以产生新一代的一组解。重复上述过程，直到满足指定的收敛要求为止。

个体:

是一个数据结构，用来描述基本的遗传结构。

适应性：每个个体有一对应的适应值。在优化问题中，适应值来自于一个估计函数。

群体:由个体组成的集合。

遗传操作：遗传操作作用于群体而产生新的群体。标准的遗传操作一般包括选择(或复制)，交叉(或重组)和变异三种基本形式。

遗传算法的五大要素：

参数编码、初始群体设定、适应度函数设计、遗传操作设计、控制参数设定。

类比自然选择，遗传算法中，我们确保种群中较好的状态有较大概率参与下一代的繁殖，而较差的状态能够繁殖自己后代的概率较小，我们使用适应度函数来评价种群中的状态，而在这里我们使用不相互攻击的皇后的对数 作为适应度函数。

类比有性繁殖，我们将要配对的个体，在字符串中随机选择一个杂交点，配对的个体所产生的后代其杂交点前后的状态信息（基因）分别来自于两个参与配对的个体。

对于整个种群，适应较强的个体其状态信息的一部分也是较优的，也即模式是较优的。较优的模式进行组合，那么我们更容易得到一个整体最优的后代。

最后，还模拟了遗传过程中可能发生的变异，这一点同样是遗传算法成功的关键。

实现选择算法

这里的选择算法仍然是模拟转盘。首先按照种群中每个个体的评估函数求概率分部，并产生一个随机数来选择种群中的一个个体，一个个体的评估函数值越大，被选择的概率就越大。

实现交叉互换

产生两个交叉点，交叉点各个部分的值相互交换。

​ c1 = x.substr(0, point1) + y.substr(point1, point2 - point1) + x.substr(point2);

​ c2 = y.substr(0, point1) + x.substr(point1, point2 - point1) + y.substr(point2);

实现变异算法

对于每个对象所具有的排列属性的每一个值，进行随机变异，该对象可能不发生变异，也可能发生2处以上的变异。

总体的遗传算法实现步骤：

1）首先初始化各种参数

2）在交叉概率的指导下发生交叉互换。

3）在变异概率的指导下发生变异。

4）更新种群。

4.测试结果

模拟退火算法：

温度下降函数	求解成功率	求解所需要的平均步数
T=0.999T	1.00	2215
T=0.99T	0.9	593
T=0.95T	0.3	239

退火越缓慢，模拟退火成功求解八皇后问题的概率就越高，但随着成功求解概率的提高，成功平均步数和失败平均步数也明显提高。

从实验中可知，只要规划好状态空间，模拟退火算法就可以进行有效的搜索，因此模拟退火算法具有很好的泛用性和稳定性。

该算法刚开始时会取大步，后续阶段取小步，因此能够在很大程度上避开局部最优解以获得全局最优解。

然而，由于要求较高的初始温度、较慢的降温速率、较低的终止温度，以及各温度下足够多次的抽样，因此优化过程较长。其次，各个指标参数随着问题的不同需要发生变化，没有广泛适用的参数，在求解实际问题时需要花时间来寻找比较适合的参数。

普通遗传算法：

交叉概率	变异概率	种群大小	找到解的概率	成功找到解需要的世代数目
0.6，下同	0.05	4	0.33	7501
	0.1	4	0.66	4320
	0.01	4	0.27	2017
	0.05	10	0.66	1385
	0.1	10	0.7	3409
	0.05	20	1.00	3371
	0.1	20	1.00	1645
	0.05	50	1.00	1327
	0.1	50	1.00	2917
0.3，下同	0.1	4	0.4	3456
	0.05	10	0.4	3867
	0.1	10	0.4	2255
	0.05	20	0.9	2165
	0.1	20	0.7	1629
	0.01	20	0.9	2688

分析表格可知：

交叉概率过小时，找到解的概率会降低很多，这是因为交叉概率过小时，经常会导致搜索阻滞，事实上交叉概率太高的话也会导致优良基因结构的丢失速度上升。

种群的大小也是影响搜索的一个重要因素，大的种群群体增加了计算量和运行时间，使得效率降低，而种群较小时，搜索空间不够足大，优良的基因结构也得不到保留，本次实验种群大小设置为20比较好。

变异概率也是影响搜索的一个重要因素。变异概率太小，使得某些基因过早丢失的信息无法回复；变异概率太高，遗传算法将变为随机搜索，效率大大降低。经测试本次实验的变异概率在0.05左右较为合适。

由于搜索失败的代价较高（需要遍历10000个世代），所以找到解的概率是一个很重要的衡量因素。

遗传算法很容易进入种群内所有个体都大体一样的情境，一旦进入这种情境，遗传算法的种群进化进程将立刻大大减缓。

具有内部竞争机制的遗传算法

遗传算法的改进：在此次遗传算法中，交叉互换产生两个子代个体（如果不交叉互换则采用亲本来作为子代个体），并且让这两个子代个体相互竞争，选择适应值高的作为此次产生的子代个体。

改进后的遗传算法搜索速度得到了巨大的提升！搜索所需要的世代数减少了十几倍！通常50~200代内就可以解决问题。

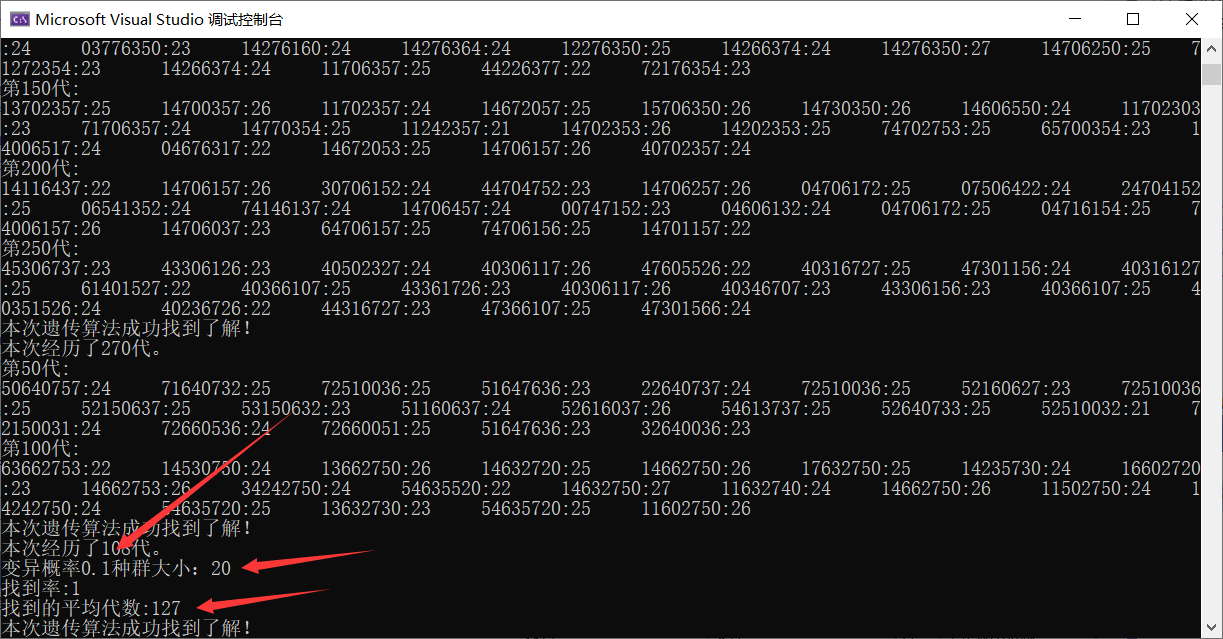
在种群内个体状态信息（基因型）很多样的时候，杂交能够进一步促进基因的多样性，此外还能变异也能产生新的基因型，所以种群内的总是能够涌现出当前种群中没有的新基因型，一旦新的基因型适应能力更强，那么新的基因型将很容易在种群中传播开。

一旦种群内个体状态信息（基因型）大部分都相似的时候，往往杂交所得后代基因型也与父母的基因型没有太大差别，此时种群要产生新的基因型只能依靠变异，而变异又应该是小概率的，这就使得种群的进化几乎停滞了。

遗传算法很容易进入所有个体都基本一样的情境实际上也和基因过于简单有关。而现实生活中变异发生的概率虽然低，但是因为基因数量很大，所以在父母和后代之间，基因型几乎比如发生了变化，所以在八皇后实验中，设置较高的变异概率也可视为一种对现实环境的更贴切的模拟，而不是书上推荐的0.005~0.01，而这也确实提高了遗传算法的效率。

而遗传算法得到改进后，效率得到明显提升，此时的参数为：种群规模20，变异概率0.1，交叉概率0.6，并且在子代产生过程中加入了竞争机制。

更多的细节和代码实现请访问我的github获取。