第6章财政收入影响因素分析及预测模型

1、背景与挖掘目标

1.1 原始数据情况

在我国现行的分税制财政管理体制下，地方财政收人不仅是国家财政收入的重要组成部分，而且具有其相对独立的构成内容。如何有效的利用地方财政收入，合理的分配，来促进地方的发展，提高市民的收入和生活质量是每个地方政府需要考虑的首要问题。因此，对地方财政收人进行预测，不仅是必要的，而且也是可能的。科学、合理地预测地方财政收人，对于克服年度地方预算收支规模确定的随意性和盲目性，正确处理地方财政与经济的相互关系具有十分重要的意义。

某市作为改革开放的前沿城市，其经济发展在全国经济中的地位举足轻重。目前，该市在财政收入规模、结构等方面与北京、上海、深圳等城市仍有一定差距，存在不断完善的空间。本案例旨在通过研究，发现影响该市目前以及未来地方财源建设的因素，并对其进行深入分析，提出对该市地方财源优化的具体建议，供政府决策参考，同时为其他经济发展较快的城市提供借鉴。

考虑到数据的可得性，本案例所用的财政收入分为地方一般预算收入和政府性基金收入。地方一般预算收入包括：

　　　　(1)税收收入，主要包括企业所得税和地方所得税中中央和地方共享的40%，地方享有的 25%的增值税、营业税、印花税等；

　　　　(2)非税收入，包括专项收入、行政事业性收费、罚没收入、国有资本经营收入和其他收入等。政府性基金收入是国家通过向社会征收以及出让土地、发行彩票等方式取得收入，并专项用于支持特定基础设施建设和社会事业发展的收入。

由于1994年我国对财政体制进行了重大改革，开始实行分税制财政体制，影响了财政收入相关数据的连续性，在1994年前后不具有可比性。由于没有合适的数学手段来调整这种数据的跃变，仅对1994年及其以后的数据进行分析，本案例所用数据均来自《某市统计年鉴》(1995-2014)。

某市1994-2013年财政收入以及相关因素的数据

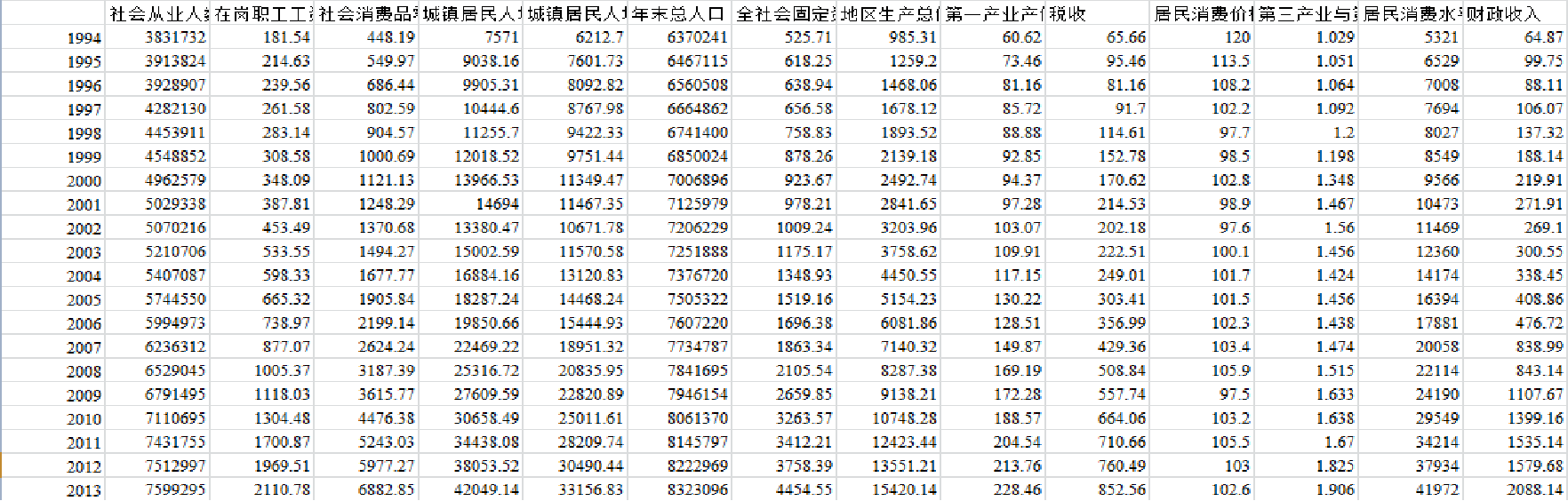
1.2 挖掘目标

（1）分析、识别影响地方财政收入的关键属性；
（2）预测2014年和2015年的财政收入。

2、分析方法与过程

2.1 初步分析

在以往的文献中，大多先建立财政收入与各待定的影响因素之间的多元线性回归模型，运用最小二乘估计方法来估计回归模型的系数，通过系数来检验它们之间的关系，模型的结果对数据的依赖程度很大，并且普通最小二乘估计求得的解往往是局部最优解。

Lasso是近年来被广泛应用于参数估计和变量选择的方法之一，并且Lasso进行变量选择在确定的条件下已经被证明是一致的。案例选用了Lasso特征选择方法来研究地方财政收入与各因素之间的关系。

2.2 基于数据挖掘技术的财政收入分析预测模型流程步骤如下

step1：对原始数据进行探索性分析，了解原始属性之间的相关性
step2：利用Lasso特征选择模型进提取关键属性
step3：建立单个属性的灰色预测模型以及支持向量回归预测模型
step4：使用支持向量回归预测模型得出2014-2015年财政收入的预测值
step5：对上述建立的财政收入预测模型进行评价

2.3 总体流程

注：Model有很多，选择最合适的，具体问题具体分析。

2.4 数据探索分析

影响财政收入(y)的因素有很多，通过经济理论对财政收入的解释以及对实践的观察，考虑一些与能源消耗关系密切并且直观上有线性关系的因素，选取以下因素为自变量，分析它们之间的关系。

社会从业人数(x1)：就业人数的上升伴随着居民消费水平的提高，从而间接影响财政收入的增加。
在岗职工工资总额(x2)：反映的是社会分配情况，主要影响财政收入中的个人所得税、房产税以及潜在消费能力。
社会消费品零售总额(x3)：代表社会整体消费情况，是可支配收入在经济生活中的实现。当社会消费品零售总额增长时，表明社会消费意愿强烈，部分程度上会导致财政收入中增值税的增　　长；同时当消费增长时，也会引起经济系统中其他方面发生变动，最终导致财政收入的增长。
城镇居民人均可支配收入(x4)：居民收入越高消费能力越强，同时意味着其工作积极性越高，创造出的财富越多，从而能带来财政收入的更快和持续增长。
城镇居民人均消费性支出(x5)：居民在消费商品的过程中会产生各种税费，税费又是调节生产规模的手段之一。在商品经济发达的如今，居民消费的越多，对财政收入的贡献就越大。
年末总人口(x6)：在地方经济发展水平既定的条件下，人均地方财政收入与地方人口数呈反比例变化。
全社会固定资产投资额(x7)：是建造和购置固定资产的经济活动，即固定资产再生产活动。主要通过投资来促进经济增长，扩大税源，进而拉动财政税收收入整体增长。
地区生产总值(x8)：表示地方经济发展水平。一般来讲，政府财政收入来源于即期的地区生产总值。在国家经济政策不变、社会秩序稳定的情况下，地方经济发展水平与地方财政收入之间存在着密切的相关性，越是经济发达的地区，其财政收入的规模就越大。
第一产业产值(x9)：取消农业税、实施三农政策，第一产业对财政收入的影响更小。
税收(x10)：由于其具有征收的强制性、无偿性和固定性特点，可以为政府履行其职能提供充足的资金来源。因此，各国都将其作为政府财政收入的最重要的收入形式和来源。
居民消费价格指数(x11)：反映居民家庭购买的消费品及服务价格水平的变动情况，影响城乡居民的生活支出和国家的财政收入。
第三产业与第二产业产值比(x12)：表示产业结构。三次产业生产总值代表国民经济水平，是财政收入的主要影响因素，当产业结构逐步优化时，财政收入也会随之增加。
居民消费水平(x13)：在很大程度上受整体经济状况GDP的影响，从而间接影响地方财政收入。

第一步：描述分析

对已有数据进行描述性统计分析，获得对数据的整体性认识。

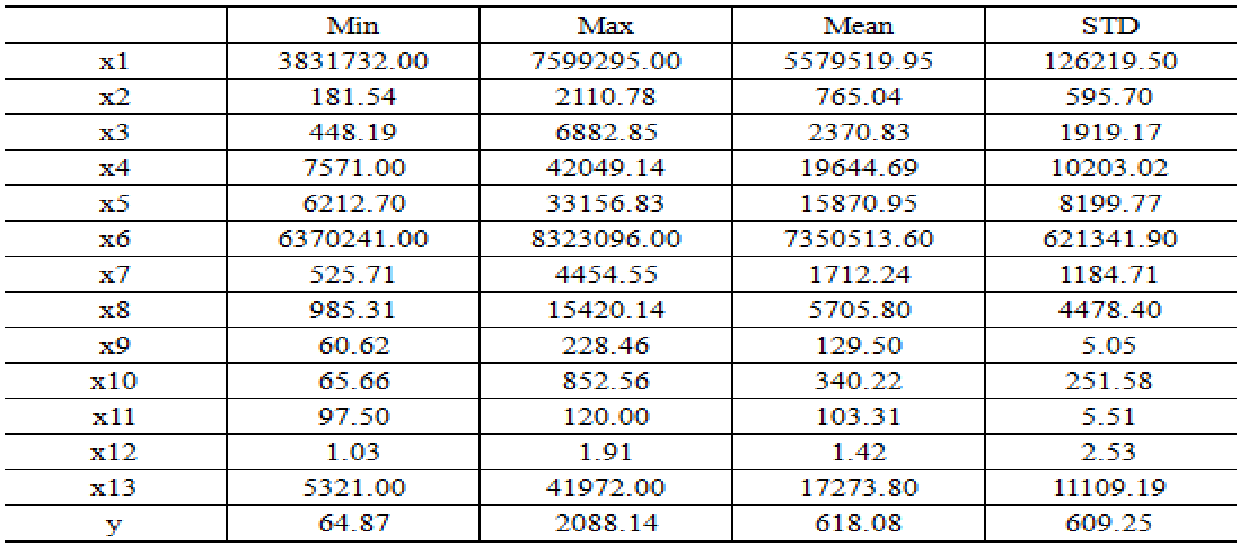
可见财政收入（y）的均值和标准差分别为618.08和609.25，这说明:第一，某市各年份财政收入存在较大差异。第二，2008年后，某市各年份财政收入大幅上升。

第二步：相关分析

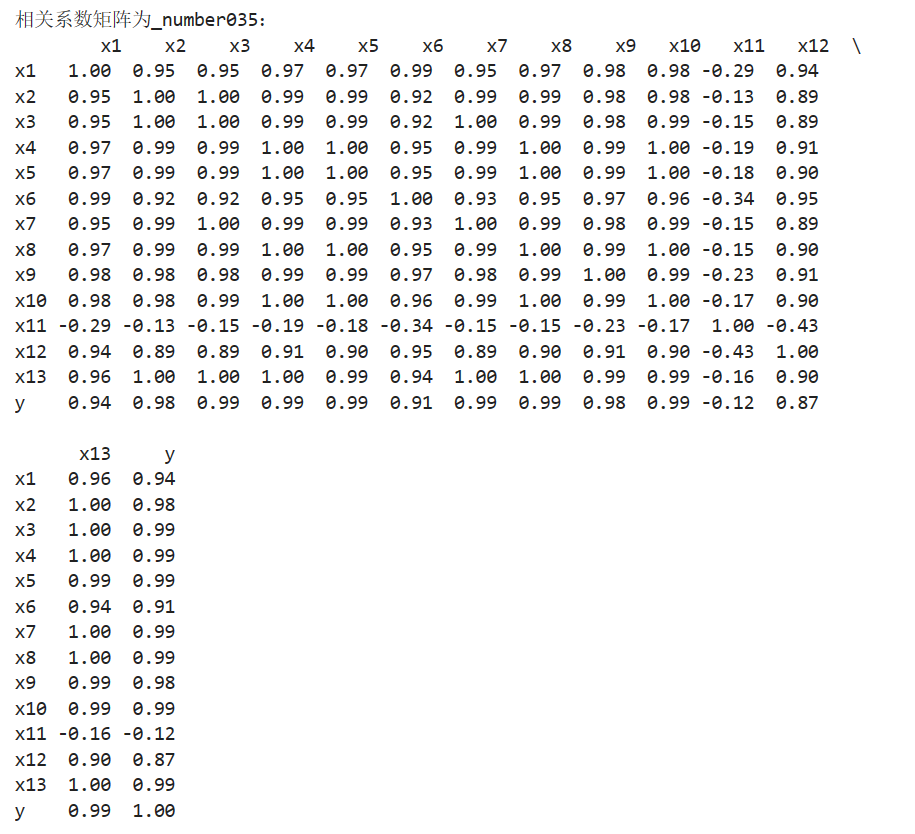
相关系数可以用来描述定量变量之间的关系，初步判断因变量与解释变量之间是否具有线性相关性。

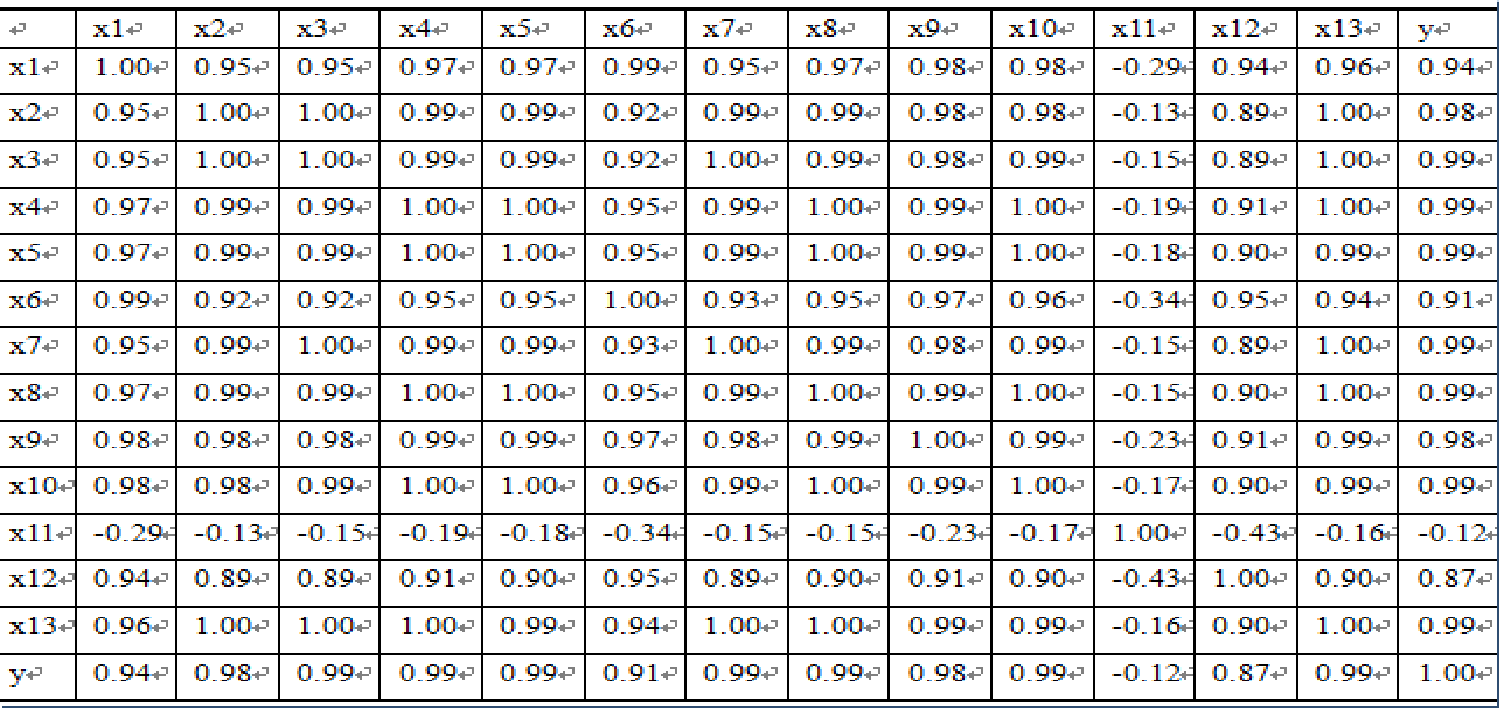
由相关矩阵可以看出居民消费价格指数(x11) 与财政收入的线性关系不显著，而且呈现负相关。其余变量均与财政收入呈现高度的正相关关系。

第三步：变量选择

运用Lasso回归方法进行关键属性选取，用Python编制相应的程序后运行得到如下结果。

可看出，在岗职工工资总额、年末总人口、税收、居民消费价格指数、第三产业与第二产业产值比等因素的系数为0，即在模型建立的过程中这几个变量被剔除了。由于某市存在流动人口与外来打工人口多的特性，年末总人口并不显著影响某市财政收入；居民消费价格指数与财政收入的相关性太小以致可以忽略；由于农牧业各税在各项税收总额中所占比重过小，而且该市于2005年取消了农业税，其他变量被剔除均有类似于上述的原因。

利用Lasso回归方法识别影响财政收入的关键影响因素是社会从业人数（x1）、社会消费品零售总额（x3）、城镇居民人均可支配收入（x4）、城镇居民人均消费性支出（x5）、全社会固定资产投资额（x7）、地区生产总值（x8）、第一产业产值（x9）和居民消费水平（x13）

财政收入及各类别收入预测模型:

某市财政收入预测模型对Lasso 变量选择方法识别的影响财政收入的因素建立灰色预测预测模型, Python及流行的扩展库并没有提供灰色预测功能，因此自行编写灰色预测函数（GM11.py）。预测结果的精度等级见下表。

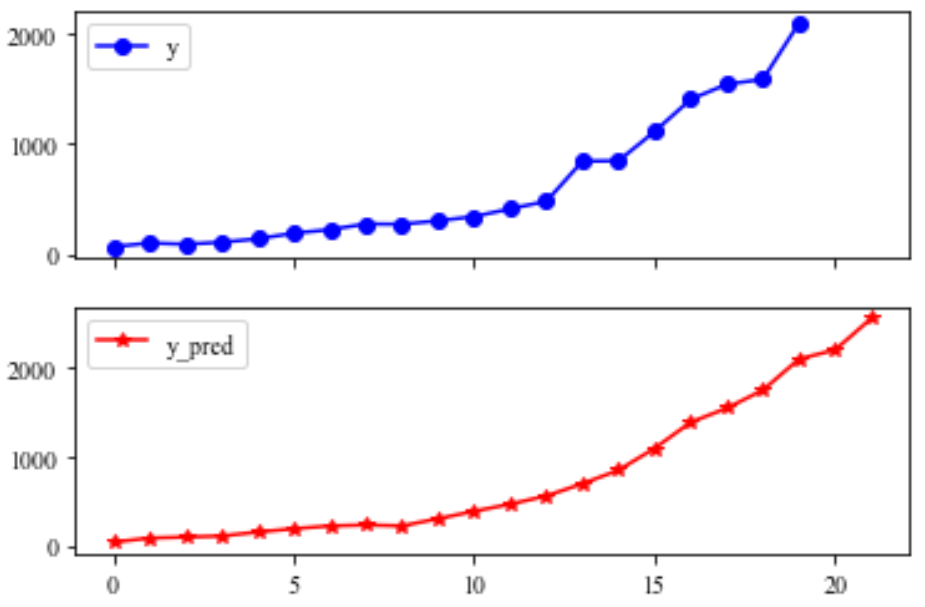
将上表预测结果代入地方财政收入建立的支持向量回归预测模型，得到1994年至2015年财政收入的预测值，如表所示：

同时得到地方财政收入真实值与预测值对比图：

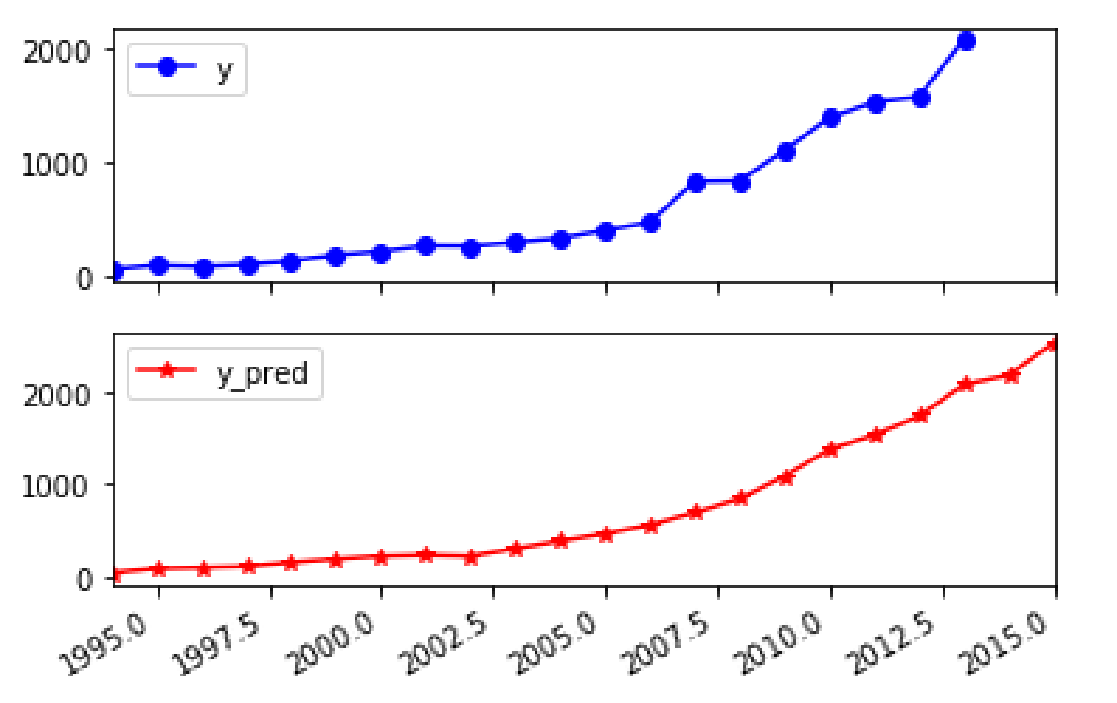
采用回归模型评价指标对地方财政收入的预测值进行评价，得到的结果如下表所示：

平均绝对误差与中值绝对误差较小，可解释方差值与R方值十分接近1，表明建立的支持向量回归模型拟合效果优良，可以用于预测财政收入。

3、上机实验

第一步描述分析

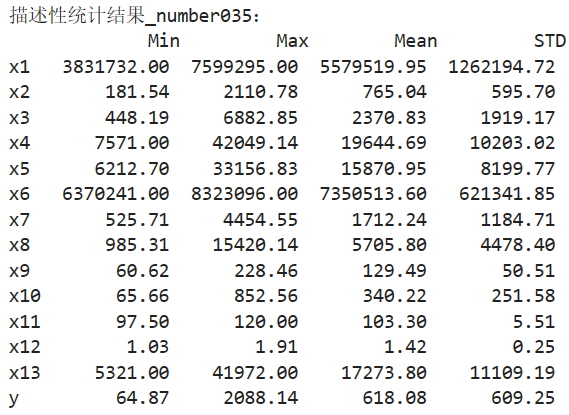
代码如下

import numpy as np
import pandas as pd

inputfile = '../chap6/data.csv' # 输入的数据文件
data = pd.read_csv(inputfile) # 读取数据

# 描述性统计分析
description = [data.min(), data.max(), data.mean(), data.std()]  # 依次计算最小值、最大值、均值、标准差
description = pd.DataFrame(description, index = ['Min', 'Max', 'Mean', 'STD']).T  # 将结果存入数据框
print('描述性统计结果_number035：\n',np.round(description, 2))  # 保留两位小数

第二步相关分析

# 相关性分析
corr = data.corr(method = 'pearson')  # 计算相关系数矩阵
print('相关系数矩阵为_number035：\n',np.round(corr, 2))  # 保留两位小数

接下来是作图：

对于分析相关关系，一般有两种常见的图形，一种是散点图，一种是热力图。

散点图：可以清晰看到各个坐标点的分布及趋势，对于数据分析者而言，其可以更直观地了解各个维度数据之间的关系，但这种方法也有缺点，即不适合大数据量，因为数据量太大，生成图片速度会很慢，同时图片太多不利于观察；
热力图：更多从数值或颜色方面，来准确描述各个维度的关系，其传递的信息较少，但比较适合大数据量。

散点图

对于多维数据，需要计算两两之间的相关性

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as stats

# 导入数据
data = pd.read_csv('../chap6/data.csv',encoding='utf-8')
# 相关性计算
print(data.corr())
# 绘图
fig = pd.plotting.scatter_matrix(data,figsize=(6,6),c ='blue',marker = 'o',diagonal='',alpha = 0.8,range_padding=0.2)  # diagonal只能为'hist'/'kde'
plt.show()

注：pandas的corr()函数只能计算相关系数r，无法计算p值。

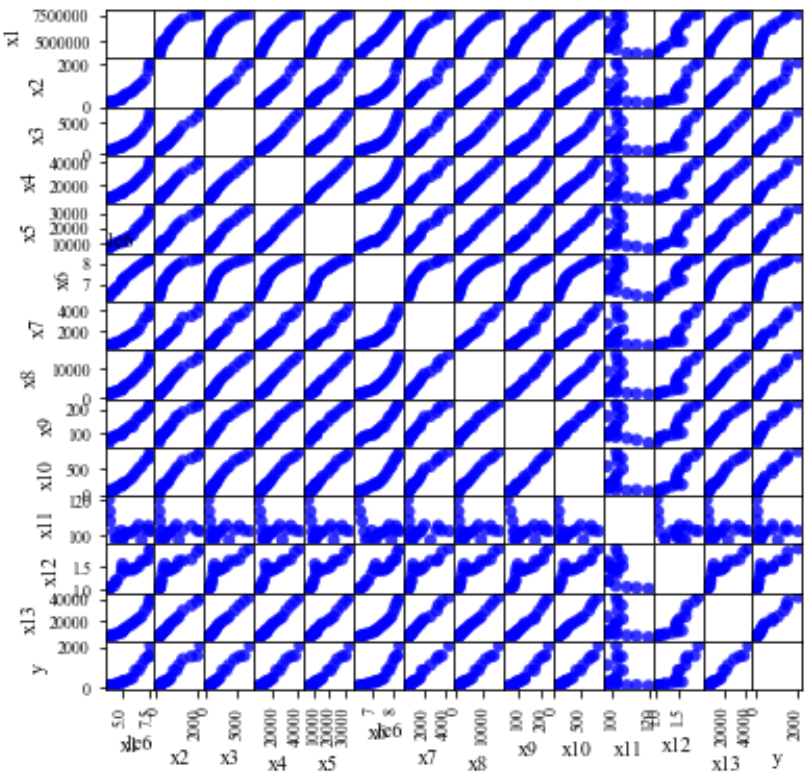
由图可见，x11对应的行和列的相关性不显著（较低）

热力图

# 绘制热力图
import matplotlib.pyplot as plt
import seaborn as sns
plt.subplots(figsize=(10, 10)) # 设置画面大小 
plt.rcParams['font.sans-serif'] = ['SimHei']
sns.heatmap(corr, annot=True, vmax=1, square=True, cmap="Blues") 
plt.title('相关性热力图 number035')
plt.show()
plt.close

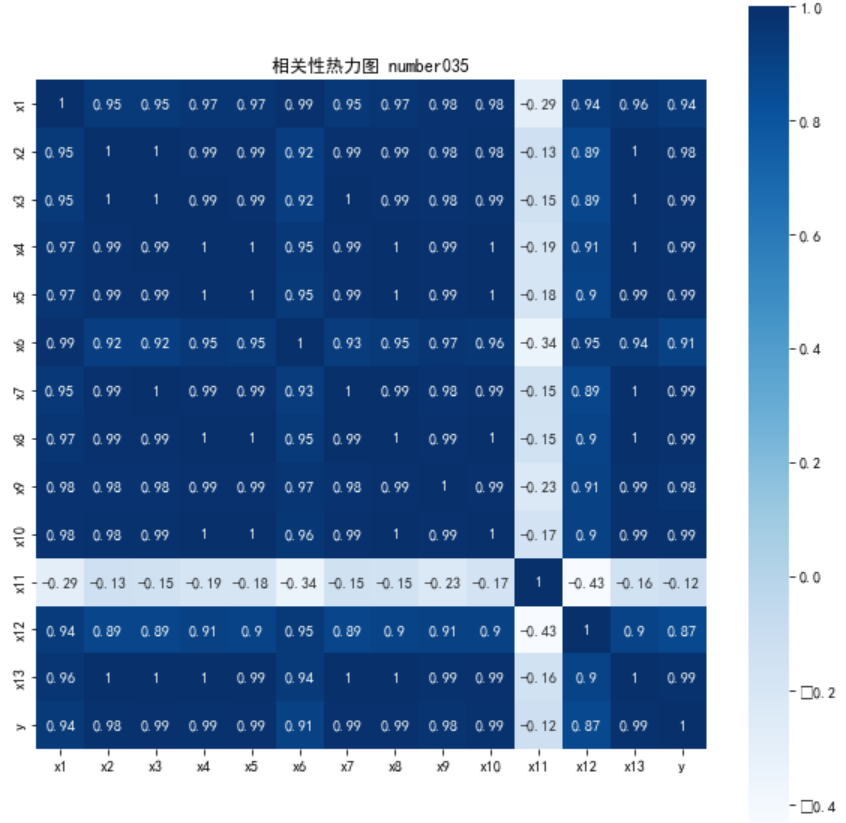
注：

sns.heatmap(glue, annot=True, linewidth=.5)

annot：格子中是否有数字标记
linewidth：各个格子间的缝隙

第三步变量选择

Lasso的优化目标：

(1 / (2 * n_samples)) * ||y - Xw||^2_2 + alpha * ||w||_1

官网：sklearn.linear_model.Lasso — scikit-learn 1.2.1 documentation

目标：求出w

处理数据的思路：通过Lasso()函数，计算相关系数非零的个数，只考虑True的类型，把非零的留下，把零的（非主要因素）去掉

import numpy as np
import pandas as pd
from sklearn.linear_model import Lasso

inputfile = '../chap6/data.csv'  # 输入的数据文件
data = pd.read_csv(inputfile)  # 读取数据
lasso = Lasso(1000)  # 调用 Lasso()函数，设置 λ的值为1000
lasso.fit(data.iloc[:,0:13],data['y'])
print('相关系数为：',np.round(lasso.coef_,5))  # 输出结果，保留五位小数

print('相关系数非零个数为：',np.sum(lasso.coef_ != 0))  # 计算相关系数非零的个数

mask = lasso.coef_ != 0  # 返回一个相关系数是否为零的布尔数组

# 通过分析发现，问题出在mask的元素个数上，mask = lasso.coef_!=0可以得到mask具有13个元素，但在new_reg_data = data.iloc[:, mask]中data具有14个column，元素个数不匹配，因此导致index error。
# 解决方案：添加一行mask = np.append(mask,True)，将mask的元素补齐到14个。
mask = np.append(mask,True)
print('相关系数是否为零：',mask)

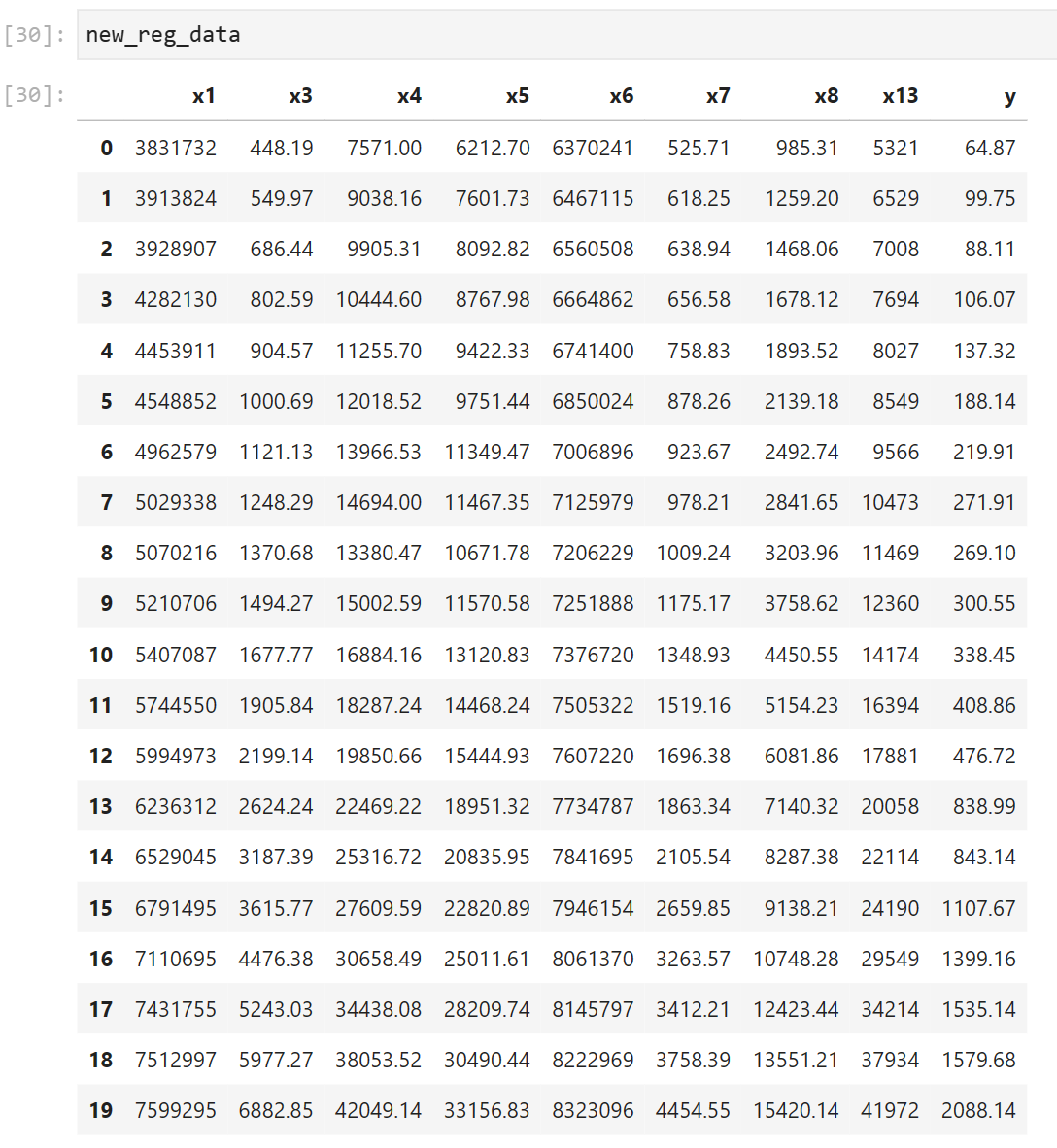
outputfile ='../new_reg_data.csv'  # 输出的数据文件
new_reg_data = data.iloc[:, mask]  # 返回相关系数非零的数据
new_reg_data.to_csv(outputfile)  # 存储数据
print('输出数据的维度为：',new_reg_data.shape)  # 查看输出数据的维度

并且也输出了new_reg_data.csv 数据文件，见下：

将lambda设为1万时，最后的维数更少了

lasso = Lasso(10000)  # 调用 Lasso()函数，设置 λ的值为10000
lasso.fit(data.iloc[:,0:13],data['y'])
print('相关系数为：',np.round(lasso.coef_,5))  # 输出结果，保留五位小数

print('相关系数非零个数为：',np.sum(lasso.coef_ != 0))  # 计算相关系数非零的个数

mask = lasso.coef_ != 0  # 返回一个相关系数是否为零的布尔数组

# 通过分析发现，问题出在mask的元素个数上，mask = lasso.coef_!=0可以得到mask具有13个元素，但在new_reg_data = data.iloc[:, mask]中data具有14个column，元素个数不匹配，因此导致index error。
# 解决方案：添加一行mask = np.append(mask,True)，将mask的元素补齐到14个。
mask = np.append(mask,True)
print('相关系数是否为零：',mask)
outputfile ='../new_reg_data10000.csv'  # 输出的数据文件
new_reg_data = data.iloc[:, mask]  # 返回相关系数非零的数据
new_reg_data.to_csv(outputfile)  # 存储数据
print('输出数据的维度为：',new_reg_data.shape)  # 查看输出数据的维度

View Code

财政收入及各类别收入预测模型

　　实验要求：用多种预测模型预测2014-2016年的数据

灰色预测算法

　GM(1,1)函数

def GM11(x0): #自定义灰色预测函数
  import numpy as np
  x1 = x0.cumsum() #1-AGO序列
  z1 = (x1[:len(x1)-1] + x1[1:])/2.0 #紧邻均值（MEAN）生成序列
  z1 = z1.reshape((len(z1),1))
  B = np.append(-z1, np.ones_like(z1), axis = 1)
  Yn = x0[1:].reshape((len(x0)-1, 1))
  [[a],[b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Yn) #计算参数
  f = lambda k: (x0[0]-b/a)*np.exp(-a*(k-1))-(x0[0]-b/a)*np.exp(-a*(k-2)) #还原值
  delta = np.abs(x0 - np.array([f(i) for i in range(1,len(x0)+1)]))
  C = delta.std()/x0.std()
  P = 1.0*(np.abs(delta - delta.mean()) < 0.6745*x0.std()).sum()/len(x0)
  return f, a, b, x0[0], C, P #返回灰色预测函数、a、b、首项、方差比、小残差概率

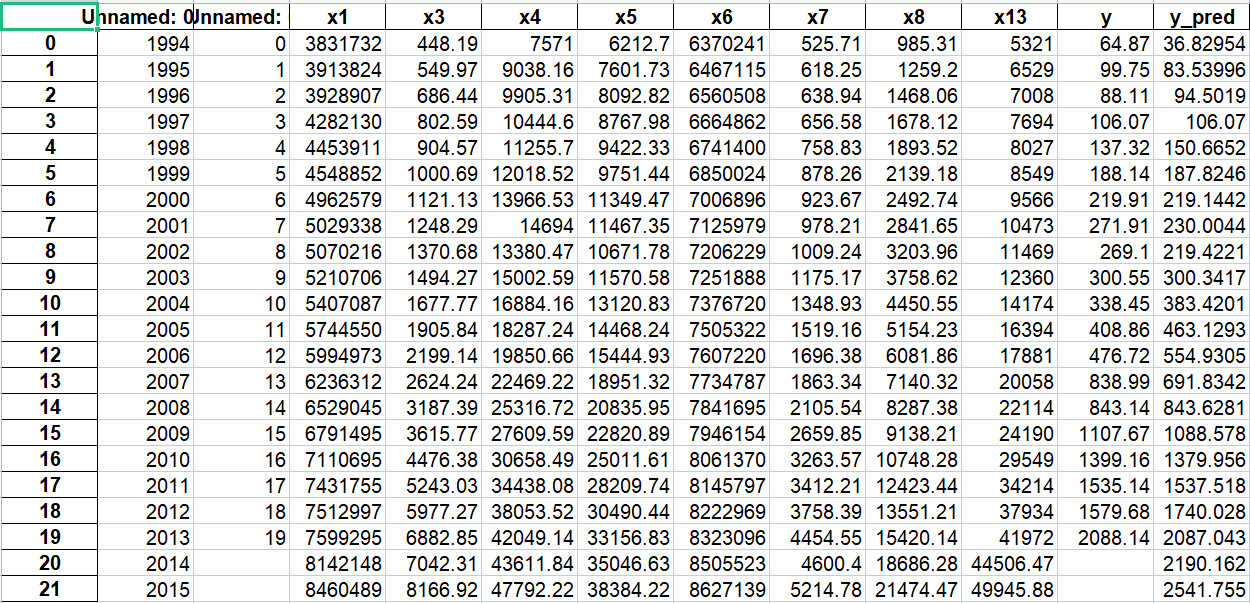
import sys
sys.path.append('../chap6')  # 设置路径
import numpy as np
import pandas as pd
from GM11 import GM11  # 引入自编的灰色预测函数

inputfile1 = '../chap6/new_reg_data.csv'  # 输入的数据文件
inputfile2 = '../chap6/data.csv'  # 输入的数据文件
new_reg_data = pd.read_csv(inputfile1)  # 读取经过特征选择后的数据
data = pd.read_csv(inputfile2)  # 读取总的数据
new_reg_data.index = range(1994, 2014)  # 作用：给数据打上标签（对应年份）

new_reg_data.loc[2014] = None
new_reg_data.loc[2015] = None
new_reg_data.loc[2016] = None

l = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']
for i in l:
  f = GM11(new_reg_data.loc[range(1994, 2014),i].values)[0]  # 取0，即只取预测值#rx_注意：正确的写法应该为.values，它是dataframe类对象的一个属性，不是方法。
  new_reg_data.loc[2014,i] = f(len(new_reg_data)-1)  # 2014年预测结果
  new_reg_data.loc[2015,i] = f(len(new_reg_data))  # 2015年预测结果
  new_reg_data.loc[2016,i] = f(len(new_reg_data)+1)  # 2016年预测结果
  new_reg_data[i] = new_reg_data[i].round(2)  # 保留两位小数
outputfile = '../chap6/new_reg_data_GM11_2016.xls'  # 灰色预测后保存的路径
y = list(data['y'].values)  # 提取财政收入列，合并至新数据框中
y.extend([np.nan,np.nan,np.nan])

生成文件

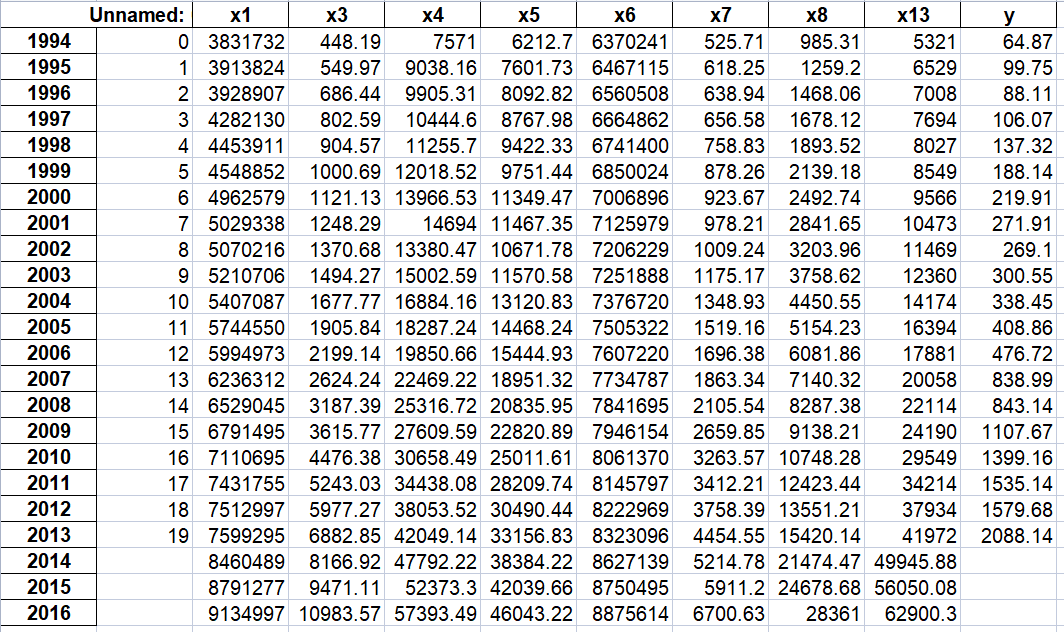
查看此时的y：

注意

y.extend([np.nan,np.nan,np.nan])

此句很重要！本人就因为没有检查到这句而一直报错！（ValueError: Length of values (22) does not match length of index (23)）

new_reg_data['y'] = y
new_reg_data.to_excel(outputfile)  # 结果输出
print('number_035预测结果为：\n',new_reg_data.loc[2014:2016,:])  # 预测结果展示

支持向量机

import matplotlib.pyplot as plt
from sklearn.svm import LinearSVR
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

inputfile = '../chap6/new_reg_data_GM11_2016.xls'  # 灰色预测后保存的路径
data = pd.read_excel(inputfile)  # 读取数据
feature = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']  # 属性所在列
data_train = new_reg_data.loc[range(1994,2014)].copy()  # 取2014年前的数据建模

data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean)/data_std  # 数据标准化
x_train = data_train[feature].values  # 属性数据
y_train = data_train['y'].values  # 标签数据

linearsvr = LinearSVR()  # 调用LinearSVR()函数
linearsvr.fit(x_train,y_train)
x = ((data[feature] - data_mean[feature])/data_std[feature]).values  # 预测，并还原结果。
data['y_pred'] = linearsvr.predict(x) * data_std['y'] + data_mean['y']
outputfile = '../chap6/new_reg_data_GM11_revenue(1).xls'  # SVR预测后保存的结果
data.to_excel(outputfile)

print('_number 035真实值与预测值分别为：\n',data[['y','y_pred']])


fig = data[['y','y_pred']].plot(subplots = True, style=['b-o','r-*'],title= 'Forecast chart of fiscal revenue influencing factors from 2014 to 2016  _number 035')  # 画出预测结果图
# plt.title('财政收入影响因素预测图（2014-2016年） _number 035',fontsize=20)
plt.show()

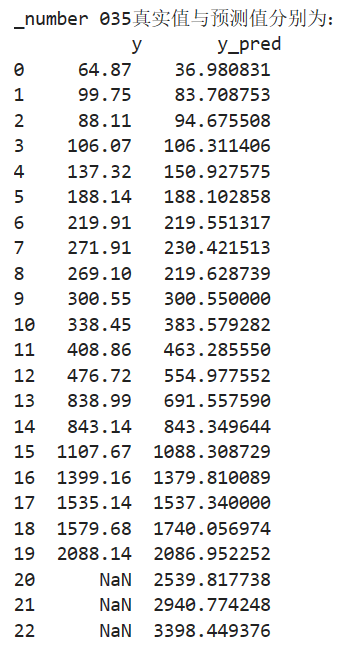
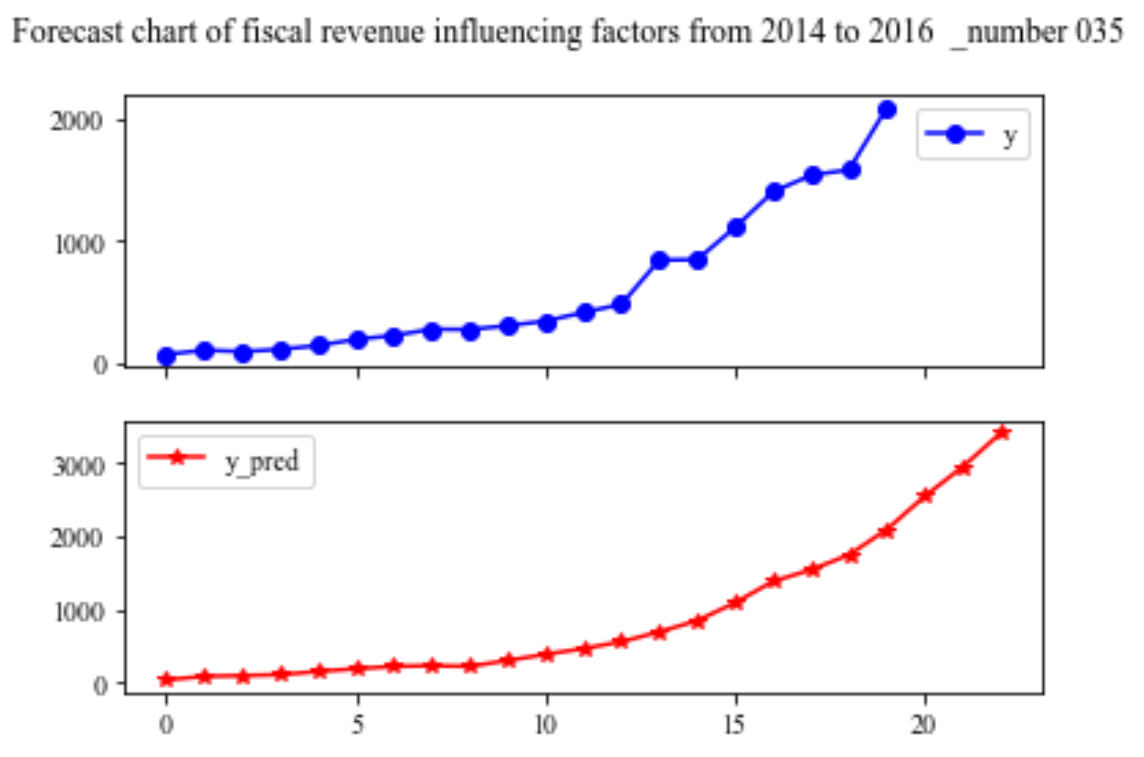
查看exel表，可获得2014~2016的财政收入预测值：

附：书中的代码及书中原题的解答

　　（1）灰色预测算法

　　GM(1,1)函数

def GM11(x0): #自定义灰色预测函数
  import numpy as np
  x1 = x0.cumsum() #1-AGO序列
  z1 = (x1[:len(x1)-1] + x1[1:])/2.0 #紧邻均值（MEAN）生成序列
  z1 = z1.reshape((len(z1),1))
  B = np.append(-z1, np.ones_like(z1), axis = 1)
  Yn = x0[1:].reshape((len(x0)-1, 1))
  [[a],[b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Yn) #计算参数
  f = lambda k: (x0[0]-b/a)*np.exp(-a*(k-1))-(x0[0]-b/a)*np.exp(-a*(k-2)) #还原值
  delta = np.abs(x0 - np.array([f(i) for i in range(1,len(x0)+1)]))
  C = delta.std()/x0.std()
  P = 1.0*(np.abs(delta - delta.mean()) < 0.6745*x0.std()).sum()/len(x0)
  return f, a, b, x0[0], C, P #返回灰色预测函数、a、b、首项、方差比、小残差概率

import sys
sys.path.append('../chap6')  # 设置路径
import numpy as np
import pandas as pd
from GM11 import GM11  # 引入自编的灰色预测函数

inputfile1 = '../chap6/new_reg_data.csv'  # 输入的数据文件
inputfile2 = '../chap6/data.csv'  # 输入的数据文件
new_reg_data = pd.read_csv(inputfile1)  # 读取经过特征选择后的数据
data = pd.read_csv(inputfile2)  # 读取总的数据
new_reg_data.index = range(1994, 2014)  # 作用：给数据打上标签（对应年份）
new_reg_data.loc[2014] = None
new_reg_data.loc[2015] = None
l = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']
for i in l:
  f = GM11(new_reg_data.loc[range(1994, 2014),i].values)[0]  # 取0，即只取预测值
    #rx_注意：正确的写法应该为.values，它是dataframe类对象的一个属性，不是方法。
  new_reg_data.loc[2014,i] = f(len(new_reg_data)-1)  # 2014年预测结果
  new_reg_data.loc[2015,i] = f(len(new_reg_data))  # 2015年预测结果
  new_reg_data[i] = new_reg_data[i].round(2)  # 保留两位小数
outputfile = '../chap6/new_reg_data_GM11.xls'  # 灰色预测后保存的路径
y = list(data['y'].values)  # 提取财政收入列，合并至新数据框中
y.extend([np.nan,np.nan])
new_reg_data['y'] = y
new_reg_data.to_excel(outputfile)  # 结果输出
print('预测结果为：\n',new_reg_data.loc[2014:2015,:])  # 预测结果展示

　　（2）SVR算法之 LinearSVR

　　注意：横向对比之后发现各个数据的量纲不同，因此必须做正则化

import matplotlib.pyplot as plt
from sklearn.svm import LinearSVR

inputfile = '../chap6/new_reg_data_GM11.xls'  # 灰色预测后保存的路径
data = pd.read_excel(inputfile)  # 读取数据
feature = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']  # 属性所在列
data_train = new_reg_data.loc[range(1994,2014)].copy()  # 取2014年前的数据建模

data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean)/data_std  # 数据标准化
x_train = data_train[feature].values  # 属性数据
y_train = data_train['y'].values  # 标签数据

linearsvr = LinearSVR()  # 调用LinearSVR()函数
linearsvr.fit(x_train,y_train)
x = ((data[feature] - data_mean[feature])/data_std[feature]).values  # 预测，并还原结果。
data['y_pred'] = linearsvr.predict(x) * data_std['y'] + data_mean['y']
outputfile = '../chap6/new_reg_data_GM11_revenue.xls'  # SVR预测后保存的结果
data.to_excel(outputfile)

print('真实值与预测值分别为：\n',data[['y','y_pred']])

fig = data[['y','y_pred']].plot(subplots = True, style=['b-o','r-*'])  # 画出预测结果图
plt.show()

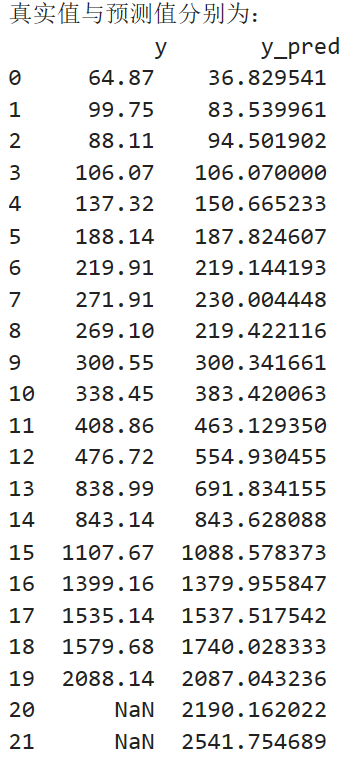
　　（3）GM(2,1) 算法

　　（4）ARIMA算法

4、拓展思考

posted @ 2023-03-01 10:42 乘着风·轻舟过阅读(3235) 评论(0) 收藏举报

刷新页面返回顶部

Carpe diem

Seize the day

第6章财政收入影响因素分析及预测模型

1、背景与挖掘目标

1.1 原始数据情况

1.2 挖掘目标

2、分析方法与过程

2.1 初步分析

2.2 基于数据挖掘技术的财政收入分析预测模型流程步骤如下

2.3 总体流程

2.4 数据探索分析

第一步：描述分析

第二步：相关分析

第三步：变量选择

财政收入及各类别收入预测模型:

3、上机实验

第一步描述分析

第二步相关分析

散点图

热力图

第三步变量选择

财政收入及各类别收入预测模型

（1）灰色预测算法

（2）SVR算法之 LinearSVR

（3）GM(2,1) 算法

（4）ARIMA算法

4、拓展思考

公告

Carpe diem

Seize the day

第6章 财政收入影响因素分析及预测模型

1、背景与挖掘目标

1.1 原始数据情况

1.2 挖掘目标

2、分析方法与过程

2.1 初步分析

2.2 基于数据挖掘技术的财政收入分析预测模型流程步骤如下

2.3 总体流程

2.4 数据探索分析

第一步：描述分析

第二步：相关分析

第三步：变量选择

财政收入及各类别收入预测模型:

3、上机实验

第一步 描述分析

第二步 相关分析

散点图

热力图

第三步 变量选择

财政收入及各类别收入预测模型

（1）灰色预测算法

（2）SVR算法 之 LinearSVR

（3）GM(2,1) 算法

（4）ARIMA算法

4、拓展思考

公告

第6章财政收入影响因素分析及预测模型

第一步描述分析

第二步相关分析

第三步变量选择

　　（1）灰色预测算法

　　（2）SVR算法之 LinearSVR

　　（3）GM(2,1) 算法

　　（4）ARIMA算法