树形DP 树的重心

树形DP 树的重心

给定一颗树，树中包含 \(n\) 个结点（编号 \(1 \sim n\)）和 \(n-1\) 条无向边。

请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式

第一行包含整数 \(n\)，表示树的结点数。

接下来 \(n-1\) 行，每行包含两个整数 \(a\) 和 \(b\)，表示点 \(a\) 和点 \(b\) 之间存在一条边。

输出格式

输出一个整数 \(m\)，表示将重心删除后，剩余各个连通块中点数的最大值。

数据范围

\(1 \le n \le 10^5\)

输入样例

9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6

输出样例：

4

参考：【E32 树形DP 树的重心】

如何判断出 “剩余各个连通块中点数的最大值最小” ？

只需要判断，假设删除结点 \(u\)，则遍历 \(u\) 的所有子树找到最大子树，记为 \(size\)。

那么 \(u\) 上面的子树怎么算呢？

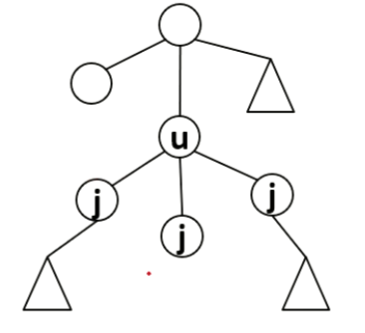
从该图可以看出，我们可以找到以 \(u\) 为根的子树全部结点数，其值为 \(sum\)，由于多了一个 \(u\)，\(sum\) 可以初始化为1，再遍历加上 \(u\) 所有子树结点数之和。

\(u\) 上面的结点数即为 \(n-sum\)。

最后来一手 ans = min(ans, max(size, n - sum)) 收工。

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 5;
const int M = 2e5 + 5;
int n, ans = N;// ans为各个连通块中点数的最大值，初始为N最大
int idx, h[N];
struct edge {int v, ne;};
edge e[M];

void add(int a, int b)
{
	e[idx] = {b, h[a]};
	h[a] = idx++;
}

int dfs(int u, int fa)
{
	int size = 0;
	int sum = 1;// 记录以u为根的最大字数结点数，若sum=1，说明为叶子结点
	for (int i = h[u]; ~i; i = e[i].ne) {
		int v = e[i].v;
		if (v == fa) continue;// 避免向上查找
		int s = dfs(v, u);// s记录以v为根的子树的结点数
		size = max(size, s);// 记录u的最大子树的结点数
		sum += s;// 累加u的各个子树的结点数
	}
	ans = min(ans, max(size, n - sum));
	return sum;
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	
	memset(h, -1, sizeof(h));
	cin >> n;
	for (int i = 1; i < n; i++) {
		int a, b; cin >> a >> b;
		add(a, b);
		add(b, a);
	}
	dfs(1, 0);
	cout << ans << '\n';
	return 0;
}