数字逻辑 可编程阵列逻辑（PAL）

数字逻辑 可编程阵列逻辑（PAL）

参考书籍：数字逻辑基础与Verilog设计 原书第3版

P402

这里先给个可编程逻辑阵列（PLA）的例子。

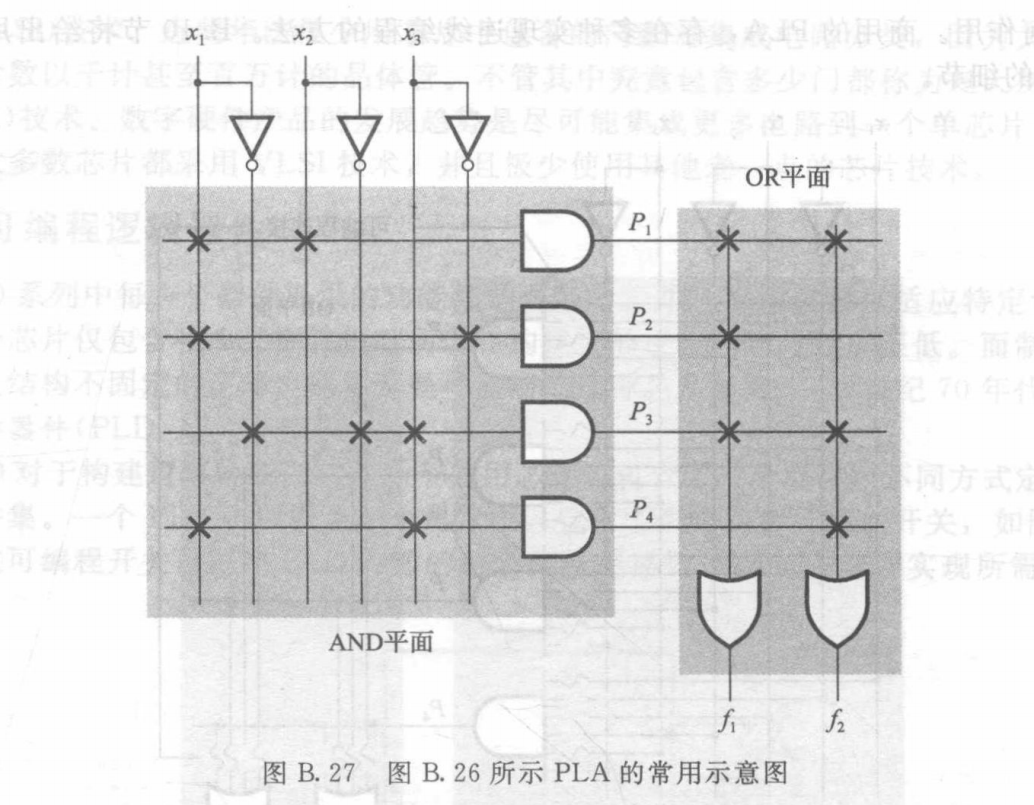
PLA的常用示意图中画X的就是选中的。

所以图 B.27 的计算过程为：

\[\begin{align} P_1=& \ x_1x_2\\[1mm] P_2=& \ x_1 \overline x_{3}\\[1mm] P_3=& \ \overline x_1 \overline x_2x_3\\[1mm] P_4=& \ x_1x_3\\[1mm] \end{align} \]

则， 对应的 \(f_1, f_2\) 为：

\[\begin{align} f_1 &=\ P_1+P_2+P_3\\[1mm] &=\ x_1x_2+x_1 \overline x_{3}+\overline x_1 \overline x_2x_3 \\[3mm] f_2 &=\ P_1+P_3+P_4\\[1mm] &= \ x_1x_2+\overline x_1 \overline x_2\ x_3+x_1x_3\\[1mm] \end{align} \]

下面讲PAL。

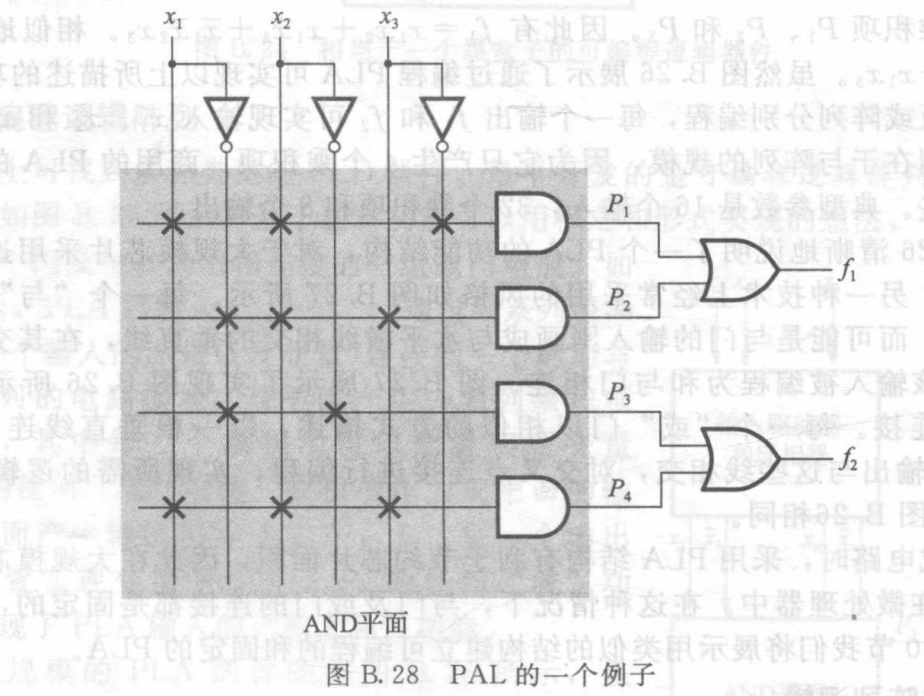
同样，PAL中画X的就是选中的。

所以图 B.28 的计算过程为：

\[\begin{align} P_1=& \ x_1x_2\overline x_{3}\\[1mm] P_2=& \ \overline x_1 x_2x_3\\[1mm] P_3=& \ \overline x_1 \overline x_2\\[1mm] P_4=& \ x_1x_2x_3\\[1mm] \end{align} \]

则， 对应的 \(f_1, f_2\) 为：

\[\begin{align} f_1 &=\ P_1+P_2\\[1mm] &=\ x_1x_2\overline x_{3}+\overline x_1 x_2x_3\\[3mm] f_2 &=\ P_3+P_4\\[1mm] &= \ \overline x_1 \overline x_2+x_1x_2x_3\\[1mm] \end{align} \]

重点是会看会列式子，不用非常熟悉。