树状数组 修改及查询操作
树状数组 修改及查询操作
常见问题:高效率地查询和维护前缀和(或区间和)。
如果数列为静态的,预处理前缀和即可。
如果数列为动态的,改变任意一个元素 \(a_k\) 的值,都会影响后续前缀和的值。
树状数组可以有效解决此类问题。
lowbit操作
lowbit就是对于十进制数 \(x\) ,有
int lowbit(x) {
return x & -x;
}
比如 lowbit(20)
1 0 1 0 0 <- 20
& 0 1 1 0 0 <- -20 = 20各位取反 + 1
------------------
0 0 1 0 0 <- lowbit(20) = 4
可以发现,lowbit操作就是找到 \(x\) 的二进制数的最后一个1,其余全抹成0。
该操作是为了爬链,下面的图展示了树状数组修改和查询。

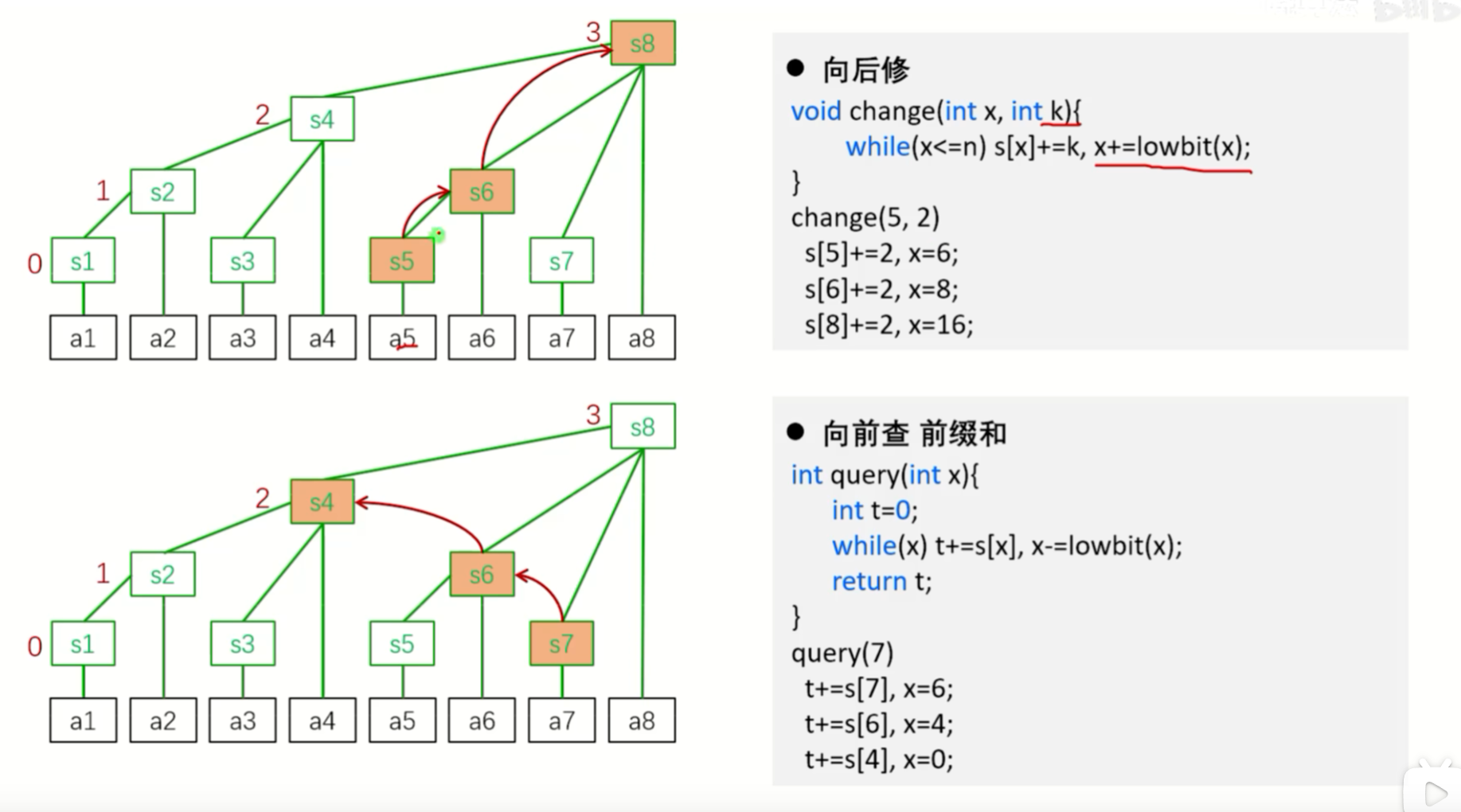
参考:【董晓算法 C81【模板】树状数组 点修+区查 区修+点查】https://www.bilibili.com/video/BV17N4y1x7c6?vd_source=d99da713618691ba36ec8e0d718ce6e7
单点修改 + 区间查询
P3374 【模板】树状数组 1
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某一个数加上 \(x\)
-
求出某区间每一个数的和
输入格式
第一行包含两个正整数 \(n,m\),分别表示该数列数字的个数和操作的总个数。
第二行包含 \(n\) 个用空格分隔的整数,其中第 \(i\) 个数字表示数列第 \(i\) 项的初始值。
接下来 \(m\) 行每行包含 \(3\) 个整数,表示一个操作,具体如下:
-
1 x k含义:将第 \(x\) 个数加上 \(k\) -
2 x y含义:输出区间 \([x,y]\) 内每个数的和
输出格式
输出包含若干行整数,即为所有操作 \(2\) 的结果。
输入输出样例 #1
输入 #1
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4
输出 #1
14
16
说明/提示
【数据范围】
对于 \(30\%\) 的数据,\(1 \le n \le 8\),\(1\le m \le 10\);
对于 \(70\%\) 的数据,\(1\le n,m \le 10^4\);
对于 \(100\%\) 的数据,\(1\le n,m \le 5\times 10^5\)。
数据保证对于任意时刻,\(a\) 的任意子区间(包括长度为 \(1\) 和 \(n\) 的子区间)和均在 \([-2^{31}, 2^{31})\) 范围内。
样例说明:
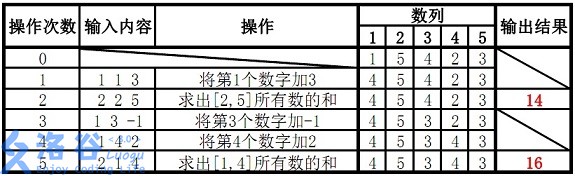
故输出结果14、16
代码
// 树状数组单点修改
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int n, m;
const int N = 5e5 + 5;
int a[N];
int s[N];
int lowbit(int x) {
return x & -x;
}
void update(int x, int k)// 更新单点
{
while (x <= n) {s[x] += k; x += lowbit(x);}
}
int sum(int x)// 输出前缀和
{
int t = 0;
while (x) {t += s[x], x -= lowbit(x);}
return t;
}
int main()
{
cin >> n >> m;
int op, x, y;
// 初始化
for (int i = 1; i <= n; i++) {
int a; cin >> a;
update(i, a);
}
// m次操作
for (int i = 1; i <= m; i++) {
cin >> op >> x >> y;;
if (op == 1) update(x, y);
else cout << sum(y) - sum(x - 1) << endl;
}
return 0;
}
区间修改 + 单点查询
[242 AcWing] 一个简单的整数问题
题目描述
给定长度为 \(N\) 的数列 \(A\),然后输入 \(M\) 行操作指令。
第一类指令形如 C l r d,表示把数列中第 \(l \sim r\) 个数都加 \(d\)。
第二类指令形如 Q x,表示询问数列中第 \(x\) 个数的值。
对于每个询问,输出一个整数表示答案。
输入格式
第一行包含两个整数 \(N\) 和 \(M\)。
第二行包含 \(N\) 个整数 \(A[i]\)。
接下来 \(M\) 行表示 \(M\) 条指令,每条指令的格式如题目描述所示。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
数据范围
\(1 \le N,M \le 10^5\),
\(|d| \le 10000\),
\(|A[i]| \le 10^9\)
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
Q 4
Q 1
Q 2
C 1 6 3
Q 2
输出样例:
4
1
2
5
思路
我们知道直接对数组 \(a[i]\) 求前缀和是求区间和,那么对差分数组 \(D[i]\) 求前缀和就是求 \(a[i]\) 本身。
比如说给定区间 $[l, r] $,在区间内每个数加上 \(d\),那么就直接把差分数组 \(D[l]\) 加上 \(d\) ,\(D[r+1]\) 减去 \(d\)。
这样既保证了区间内的修改,有保证了区间外的稳定性。
但可以发现,没有用到差分数组,直接修改这一个区间的前缀和,实际一样的效果。
最后单点查询,直接输出该点所对应差分数组的前缀和就行。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int a[N], s[N];
int n, m;
int lowbit(int x)
{
return x & -x;
}
void update(int x, int d)
{
while (x <= n) s[x] += d, x += lowbit(x);
}
int sum(int x)
{
int t = a[x];// 注意这里t初始为a[x]
while (x) t += s[x], x -= lowbit(x);
return t;
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
while (m--) {
char c; cin >> c;
if (c == 'C') {
int l, r, d; cin >> l >> r >> d;
update(l, d);
update(r + 1, -d);
}
else {
int x; cin >> x;
cout << sum(x) << endl;
}
}
return 0;
}
区间修改 + 区间查询
[243 AcWing] 一个简单的整数问题2
题目描述
给定一个长度为 \(N\) 的数列 \(A\),以及 \(M\) 条指令,每条指令可能是以下两种之一:
C l r d,表示把 \(A[l],A[l+1],…,A[r]\) 都加上 \(d\)。Q l r,表示询问数列中第 \(l \sim r\) 个数的和。
对于每个询问,输出一个整数表示答案。
输入格式
第一行两个整数 \(N,M\)。
第二行 \(N\) 个整数 \(A[i]\)。
接下来 \(M\) 行表示 \(M\) 条指令,每条指令的格式如题目描述所示。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
数据范围
\(1 \le N,M \le 10^5\),
\(|d| \le 10000\),
\(|A[i]| \le 10^9\)
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4
输出样例:
4
55
9
15
思路
这里需要公式推导。
给定一个数 \(k\) ,要求计算 \(a_1 \sim a_k\) 所有数之和。
这里我们需要两个树状数组维护,称为二阶树状数组。
\(k\sum_{i=1}^{k}D_i\) 称为 \(s_1\) 数组,\(\sum_{i=1}^{k}(i-1)D_i\) 成为 \(s_2\) 数组。
在更改区间时,两个树状数组同时更新。
注意 \(s_2\) 的更新,更新左端点 \(l\) 时,加上 \((l-1)\times d\);更新右端点 \(r\) 时,减去 \((r+1-1)\times d=r\times d\) 。
同时注意维护的单点是 \(l\) 和 \(r+1\)。
查询时输出 \(a_1 \sim a_r\) 所有数之和 \(-\) \(a_1 \sim a_{l-1}\) 所有数之和。
!!!(更新区间是 \(l\) 和 \(r+1\) ,最后输出是 \(l-1\) 和 \(r\),一定注意)
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
typedef long long ll;
#define lowbit(x) (x & -x)
int n, m;
ll s1[N], s2[N]; // 二阶树状数组
void update1(ll x, ll d) {while (x <= n) {s1[x] += d, x += lowbit(x);}}
void update2(ll x, ll d) {while (x <= n) {s2[x] += d, x += lowbit(x);}}
ll sum1(ll x) {auto t = 0ll; while (x) {t += s1[x], x -= lowbit(x);} return t;}
ll sum2(ll x) {auto t = 0ll; while (x) {t += s2[x], x -= lowbit(x);} return t;}
int main()
{
cin >> n >> m;
ll old = 0, a;
for (int i = 1; i <= n; i++) {
cin >> a;
update1(i, a - old); // 差分1
update2(i, (i - 1) * (a - old));
old = a;
}
while (m--) {
char op; cin >> op;
if (op == 'C') {
int l, r, d; cin >> l >> r >> d;
update1(l, d);
update1(r + 1, -d);
update2(l, d * (l - 1));
update2(r + 1, -d * r); // d * r = d * (r + 1 - 1)
}
else {
int l, r; cin >> l >> r;
cout << r * sum1(r) - (l - 1) * sum1(l - 1) - (sum2(r) - sum2(l - 1)) << endl;
}
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号