绪论&第一章

内容简介

全书共分 18 章，主要内容有：电路模型和电路定律、电阻电路的等效变换、电阻电路的一般分析、电路定理、含有运算放大器的电阻电路、储能元件、一阶电路和二阶电路的时域分析、相量法、正弦稳态电路的分析、含有耦合电感的电路、电路的频率响应、三相电路、非正弦周期电流电路和信号的频谱、线性动态电路的复频域分析、电路方程的矩阵形式、二端口网络、非线性电路、均匀传输线，另有磁路和铁心线圈、PSpice 简介和 MATLAB 简介三个附录。

绪论

一、课程定位

"电路" 课程是高等学校电子与电气信息类专业的重要的基础课，是所有强电专业和弱电专业的必修课。学习本课程要求学生具备必要的电磁学和数学基础知识。

"电路" 课程以分析电路中的电磁现象，研究电路的基本规律及电路的分析方法为主要内容。

通过本课程的学习，使学生掌握电路的基本理论知识、电路的基本分析方法和初步的实验技能，为进一步学习电路理论打下初步的基础，为学习电子与电气信息类专业的后续课程准备必要的电路知识。因此，"电路" 课程在整个电子与电气信息类专业的人才培养方案和课程体系中起着承前启后的重要作用。

二、电路理论及相关科学技术的发展简史

人类对电磁现象的认识始于对静电、静磁现象的观察。1729 年，英国人S.格雷将材料分为两类 — 导体和绝缘体。美国科学家富兰克林（B.Franklin，1706 — 1790）于 1749 年提出了正电和负电的概念。1785 — 1789 年，法国人库仑（C.A.Coulomb）定量地研究了两个带电体间的相互作用，得出了历史上最早的静电学定律 — 库仑定律。

1800 年，意大利物理学家伏特（A.Vlota，1745 — 1827）发明了伏打电池，它能够把化学能不断地转变为电能，维持单一方向的持续电流。这一发明为人们深入研究电化学、电磁学以及它们的应用打下了物质基础。以后很快发现了电流的化学效应、热效应以及利用电来照明等。

1820 年，丹麦物理学家奥斯特（H.C.Oersted，1777 — 1851）通过实验发现了电流的磁效应，在电与磁之间架起了一座桥梁，打开了近代电磁学的突破口。

1825 年，法国科学家安培（A.M.Ampere，1775 — 1836）提出了著名的安培环路定律。他从 1820 年开始在测量电流的磁效应中，发现两个载流导线可以互相吸引，又可以相互排斥。这一发现成为研究电学的基本定律，为电动机的发明作了理论上的准备。

1826 年，德国人欧姆（G.S.Ohm，1787 — 1854）在多年实验基础上，提出了著名的欧姆定律：在恒定温度下，导线回路中的电流等于回路中的电动势与电阻之比。欧姆又将这一定律推广于任意一段导线上，并得出导线中的电流等于这段导线上的电压与电阻之比。

1831 年，英国物理学家法拉第（M.Faraday，1791 — 1867）发现了电磁感应现象。当他继续奥斯特的实验时，他坚信，既然电能产生磁，那么磁也能产生电。他终于发现在磁场中运动的导体会产生感生电动势，并能在闭合导体回路中产生电流。这一发现成为发电机和变压器的基本原理，从而使机械能变为电能成为可能。

1832 年，亨利提出了表征线圈中自感应作用的自感系数L。

1834 年，俄国人楞次提出感应电流方向的定律，即著名的楞次定律。

1838 年，画家出身的美国人莫尔斯（S.F.Morse，1791 — 1872）发明了电报。

1845 年，德国科学家基尔霍夫（G.R.Kirchhoff，1824 — 1887）在深入研究了欧姆的工作成果之后，提出了电路的两个基本定律 — 基尔霍夫电流定律（简称 KCL）和基尔霍夫电压定律（简称 KVL）。它是集总参数电路中电压、电流必须服从的规律。

1853 年，汤姆逊（W.Thomson，1824 — 1907，即开尔文勋爵）采用电阻、电感和电容的电路模型，分析了莱顿瓶的放电过程，得出电振荡的频率。

同年，亥姆霍兹提出电路中的等效发电机定理。

1854 年，汤姆逊发表了电缆传输理论，分析了信号的衰减、延迟、失真等现象。

1857 年，基尔霍夫考虑到架空传输线与电缆不同，得出了包括自感系数在内的完整的传输线上电压及电流方程式，称之为电报员方程或基尔霍夫方程。至此，包括传输线在内的电路理论就基本建立起来了。

1864 年，英国物理学家麦克斯韦（J.C.Maxwell，1831 — 1879）总结了当时所发现的种种电磁现象的规律，将它表达为麦克斯韦方程组，预言了电磁波的存在，为电路理论奠定了坚实的基础。

1887 年，德国物理学家赫兹（H.R.Hertz，1857 — 1894）经过艰苦的反复实验，证明麦克斯韦所预言的电磁波确实存在。

1866 年，德国工程师西门子（E.W.Siemens，1823 — 1883）发现了电动机原理并用在了发电机的改进上。

1881 年，直流高压输电试验成功。但由于直流高压不便于用户直接使用，同年在发明变压器的基础上又实现了远距离交流高压输电。从此，电气化时代开始了。

1876 年，美国科学家贝尔（A.G.Bell，1847 — — 1922）发明了电话。当时电报已很发达，贝尔在多路电报通信实验中，萌发了在电报线上通话的设想。在T.A.沃森的协助下，经过不懈的努力终于试验成功。

1879 年，美国人爱迪生（T.A.Edison，1847 — 1931）发明了炭丝灯泡。1912 年美国人W.D.库利奇发明了钨丝灯泡，成为最普及的照明用具。

1880 年，英国人J.霍普金森提出了形式上与欧姆定律相似的计算磁路用的定律。

19 世纪末，交流电技术的迅速发展，促进交流电路理论的建立。1893 年，C.P.施泰因梅茨提出分析交流电路的复数符号法（相量法），采用复数表示正弦式的交流电，简化了交流电路的计算。

瑞士数学家J.R.阿尔甘提出的矢量图，也成为分析交流电路的有力工具。

1894 年，意大利人马可尼（G.Marconi，1874 — 1937）和俄国的波波夫分别发明了无线电。从此开始了无线电通信的时代。

电真空器件的发明使电子工程的发展推进了一大步。英国科学家汤姆逊（J.J.Thomson，1856 — 1940）在 1895~1897 年间反复测试，证明了电子确实存在。

随后，英国科学家弗莱明（J.A.Fleming）在爱迪生发明的热二极管的基础上发明了实用的真空二极管。它具有单向导电特性，能用来整流或检波。

1906 年，美国人德福雷斯特（L.DeForest）发明了真空三极管，它对微弱电信号有放大作用。

1914 年，德福雷斯特用真空三极管又构成了振荡电路，使无线电通信系统更加先进。

应用的需要导致了大规模发电及输配电的出现和发展。在 19 世纪末还发生过一场 "交、直流之争"。以爱迪生为代表的一方主张应用直流电，而另一方以G.威斯汀豪斯及其创建的西屋公司为代表，主张应用交流电。直到交流发电机、感应电动机、变压器等发明之后，充分显示了交流制的优点，交流制才得到广泛的应用。

进入 20 世纪，1911 年英国工程师O.亥维赛提出阻抗的概念，还提出了求解电路瞬态过程的运算法。1918 年，福台克提出的对称分量法，简化了不对称三相电路的分析。这一方法至今仍为分析三相交流电机、电力系统不对称运行的常用方法。1920 年，G.A.坎贝尔、K.瓦格纳研究了梯形结构的滤波电路。1924 年，R.M.福斯特提出电感电容二端网络的电抗定理。此后便建立了由给定频率特性设计电路的网络综合理论。

1925 年，英国人贝尔德（J.L.Baird）首先发明电视。几乎在同时，美国无线电公司（R.C.A）的工程师兹沃雷金（V.K.Zworykin）发明了电视显像管。1933 年，他利用真空二极管、真空三极管和显像管，最早发明了电视机。1936 年，黑白电视机正式问世了。

在电子管被发明后，电子电路的技术迅速发展。1932 年瑞典人H.奈奎斯特提出了由反馈电路的开环传递函数的频率特性判断闭环系统稳定性的判据。1945 年美国人H.W.伯德出版了《网络分析和反馈放大器》一书，总结了负反馈放大器的原理，由此形成了分析线性电路和控制系统的频域分析方法，并得到广泛的应用。

1947 年 12 月 24 日，贝尔实验室的布拉顿（W.H. Brattain）、巴丁（J.Bardeen）和肖克利（W.B.Shockley）发明了一种点接触晶体管。这项发明自从 1948 年公布于世起，很快就应用于通信、电视、计算机等领域，电子技术进入了半导体时代。

1958 年发明了集成电路，它将构成电子电路的电阻、电容、二极管、晶体管和导线都制造在一块几平方毫米的半导体芯片上，从而使体积大大缩小。现在集成电路已从含几十个晶体管的小规模集成电路发展到含上下百万个晶体管的超大规模集成电路，电子技术进入了集成电路时代。

从 20 世纪 30 年代开始，电路理论已形成为一门独立的学科。建立了各种元器件的电路模型。成功地运用电阻、电容、电感、电压源、电流源等几种理想元件，近似地表征成千上万种实际电气装置。到 20 世纪 50 年代末，电路理论在学术体系上基本完善，这一发展阶段称为经典电路理论阶段。

在 20 世纪 60 年代以后，电路理论又经历了一次重大的变革，这一变革的主要起源是新型电路元件的出现和计算机的冲击，电路理论无论在深度和广度方面均得到巨大的发展。因此又称 20 世纪 60 年代以后的电路理论为近代电路理论。

近代电路理论的主要特点之一是吉尔曼（Guillemin）将图论引入电路理论之中。它为应用计算机进行电路分析和集成电路布线与板图设计等研究提供了有力的工具。特点之二是出现大量新的电路元件、有源器件，如使用低电压的MOS电路，摒弃电感元件的电路，进一步摒弃电阻的开关电容电路等。当前，有源电路的综合设计正在迅速发展之中。特点之三是在电路分析和设计中应用计算机后，使得对电路的优化设计和故障诊断成为可能，大大地提高了电子产品的质量并降低了成本。

三、电路理论的应用

电路理论是高等学校电子与电气信息类专业的技术基础课，为该类专业的后续许多课程提供理论支持，例如模拟电子技术、数字电子技术、信号与系统、电机学、电力系统分析、集成电路设计、自动控制、电力电子技术等课程都用到电路理论。

四、电路理论和 "电路" 课程

电路理论是电气工程和电子科学技术的主要理论基础，是一门研究电路分析和网络综合与设计基本规律的基础工程学科。所谓电路分析是在电路给定、参数已知的条件下，通过求解电路中的电压、电流而了解电网络具有的特性；而网络综合是在给定电路技术指标的情况下，设计出电路并确定元件参数，使电路的性能符合设计要求。因此电路分析是电路理论中最基本的部分，是学习电路理论的人门课程，被列为电类各专业共同需要的技术基础课。

第一章 电路模型和电路定律

本草介绍电路模型、电路元件的概念，电压、电流参考方向的概念，元件、电路吸收或发出功率的表达式和计算；还介绍电阻、独立电源和受控电源等电路元件。

电路中的电压、电流之间具有两种约束，一种是由电路元件决定的元件约束；另一种是元件间连接而引入的几何约束（又称拓扑约束），后者由基尔霍夫定律来表达。基尔霍夫定律是集总参数电路的基本定律。

1.1 电路和电路模型

实际电路是为完成某种预期目的而设计、安装、运行（也可以是在非预期情况，例如短路、漏电等），由电路部件（例如电阻器、蓄电池等）和电路器件（例如晶体管、集成电路等）相互连接而成的电流通路装置。实际电路常借助于电压、电流而完成传输电能或信号、处理信号、测量、控制、计算等功能。其中，电能或电信号的发生器称为电源，用电设备称为负载。由于电路中的电压、电流是在电源的作用下产生的为，因此电源又称为激励源或激励；由激励而在电路中产生的电压、电流称为响应。有时，根据激励与响应之间的因果关系，把激励称为输入，响应称为输出。

术语：

集总参数电路和分布参数电路。

部件、器件、元件、零件

电路部件、电路器件

直流：电流的大小和方向都不变。

交流：除了直流。

强电通常用来传递能量（电能）。

弱电通常用来传递信息。

同义词：

电能或电信号的发生器，电源，激励源，激励，输入。

用电设备，负载。

电压、电流，响应，输出。

本书的主要内容是介绍电路理论的入门知识并为后续课程的学习准备必要的基础。电路理论研究电路中发生的电磁现象，并用电流、电压、电荷、磁通等物理量来描述其中的过程。电路理论主要是计算电路中各部件、器件的端子电流和端子间的电压，一般不涉及内部发生的物理过程。本书讨论的对象不是实际电路而是实际电路的电路模型。实际电路的电路模型由理想电路元件相互连接而成，理想元件是组成电路模型的最小单元，是具有某种确定电磁性质并有精确数学定义的基本结构。在一定的工作条件下，理想电路元件及它们的组合足以模拟实际电路中部件、器件中发生的物理过程。在电路模型中各理想元件的端子是用 "理想导线" 连接起来的。根据元件对外端子的数目，理想电路元件可分为二端、三端、四端元件等。

理想导线的电阻为零，且假设当导线中有电流时，导线内、外均无电场和磁场。理想导线在电路模型中表现为线段。

5 种基本的理想电路元件：

电阻元件：用来表示消耗电能的元件。

电感元件：用来表示产生磁场，储存磁场能量的元件。

电容元件：用来表示产生电场，储存电场能量的元件。

电流源：用来表示将其它形式的能量转变成电能的元件。

电压源：同上。

其中，电感和电容是对偶关系。

电感和电容只储存或转移电能，不会消耗电能。

5 种基本理想电路元件有三个特征：

1. 只有两个端子；
2. 可以用电压或电流按数学方式描述，即表述为 f(u,i)；
3. 不能被分解为其他元件。

每一种理想电路元件都有其标准画法。

由电路理论的研究内容可知，在将实际部件、器件抽象为理想元件时，只关心实际部件、器件的电磁性质。电磁性质相同的不同实际器件、部件，在一定的条件下可以抽象为相同的理想元件。同一个实际部件、器件，在不同情况下，可能需要抽象为不同的理想元件。

用理想电路元件或它们的组合模拟实际器件就是建立其模型，简称建模。建模时必须考虑工作条件，并按不同准确度的要求把给定工作情况下的主要物理现象和功能反映出来。例如，一个线圈的建模：在直流情况下，它在电路中仅反映为导线内电流引起的能量消耗，因此，它的模型就是一个电阻元件；在电流变化的情况下（包括交变电流），线圈电流产生的磁场会引起感应电压，故电路模型除电阻元件还应包含一个与之串联的电感元件；当电流变化甚快时（包括高频交流），则还应计及线圈导体表面的电荷作用，即电容效应。所以其模型中还需要包含电容元件。可见，在不同的工作条件下，同一实际器件可能采用不同的模型。模型取得恰当，对电路进行分析计算的结果就与实际情况接近；模型取得不恰当，则会造成很大误差甚至导致错误的结果。如果模型取得太复杂则会造成分析困难，取得太简单则可能无法反映真实的物理现象。建模问题需要专门进行研究。

今后本书所涉及电路均指由理想电路元件构成的电路模型。同时将把理想电路元件简称为电路元件。有时把实际电路器件也称为 "电路元件"。但本书中凡涉及 "电路元件" 均指理想化模型。

通常，电路又称网络，本书中将不加区分地引用。

电路理论（或电网络理论）是一门研究网络分析和网络综合或设计的基础工程学科，它与近代系统理论有密切的关系。

本书的主要内容是电路分析，探讨电路的基本定律和定理，并讨论各种分析方法，为学习电气工程技术、电子和信息工程技术等建立必要的理论基础。

网络分析（Analysis）问题，指给定电路结构、参数求解电路性能；网络综合（Synthesis）问题，指给定电路性能要求，求电路结构、参数，是网络分析的逆问题；如果在综合过程中还考虑其他诸如灵敏度、优化、成本、工艺等因素则成为电路设计。

1.2 电流和电压的参考方向

物理量的表示：

电流：I

电压：U

电荷：Q

磁通：\(\Phi\)

磁通链：\(\Psi\)

电功率：P

电能：W

一般情况，用大写字母表示常量，用小写字母表示随时间变化的变量。即将 u(t)，i(t) 等简写为 u，i 等。

电流：带电粒子的定向运动。

电流强度：单位时间内通过导体横截面的电荷量。

电流的定义：

\[i(t) \overset{\rm def}{=} \lim_{\Delta t \to 0} \frac{\Delta q}{\Delta t} =\frac{dq}{dt} \]

电流的实际方向：正电荷的运动方向。

电势 \(\Phi\)：单位正电荷 q 在电路中，从一点移至参考点（参考点的电势为 0）时，电场力所做的功。

电压 U：单位正电荷 q 在电路中，从一点移至另一点时，电场力所做的功。

\[U \overset{\rm def}{=} \frac{dW}{dq} \]

电压的实际方向：电位真正降低的方向。

有些地方将电势记为 v，但 v 容易和 u 混淆，因此不建议。

某一点的电势和选择哪一点为参考点有关。

某两点之间的电压和选择哪一点作为参考点无关。

电压，也叫电压降，也叫两点之间的电势差。

电路中电位参考点可任意选择；参考点一经选定，电路中各点的电位值就唯一确定；当选择不同的电位参考点时，电路中各点电位值将改变，但任意两点间电压保持不变。

在电路分析中，当涉及某个元件或部分电路的电流或电压时，有必要指定电流或电压的参考方向。这是因为电流或电压的实际方向可能是未知的，也可能是随时间变动的。

下图表示电流的参考方向：

导线上标识的箭头表示电流的参考方向，参考方向是人为指定的，参考方向可以任意指定，方向是随意的，指定一个参考方向的目的就是让电流值变为代数量。

电流的参考方向有两种表示方式：

1. 可以在导线上用箭头来表达。
2. 也可以用双下标来表示，例如，\(i_{AB}\) 表示参考方向是从 A 到 B 的。

一般都只用第一种方法，第二种方法要避免使用。

只有规定了参考方向，才能写出随时间变化的电流的函数式。

虚线表示电流的实际方向。实际方向可能是从 A 到 B 的，也可能是从 B 到 A 的。

当实际方向和参考方向相同时，电流值为正；当电流的实际方向和参考方向相反时，电流值为负。于是，在指定了参考方向后，电流的正负就反映了电流的实际方向。

作为代数量的电流可以表达电流大小和电流真实方向两个信息，电流值的绝对值表达电流值的大小，电流值的正负号结合指定的电流的参考方向可以判断电流的真实方向。

同理，对电路两点之间的电压也可以指定参考方向或者参考极性。

在表示两点之间的电压时，用正极性（+）表示高电位，用负极性（-）表示低电位。正极指向负极的方向就是电压的参考方向。指定了电压的参考方向后，电压就是一个代数量。如果实际电压方向和电压的参考方向相同，则电压值为正；如果实际电压方向和电压的参考方向相反，则电压值为负。

电压的参考方向有三种表示方式：

1. 用正（+）负（-）极性表示。
2. 在电路旁边用一个带箭头的线表示。
3. 用双下标表示，例如，\(u_{AB}\) 表示 A 点和 B 点两点之间的电压，且参考方向是从 A 到 B 的。

注意：一般只用第一种方法。

一个元件的电流或电压的参考方向可以独立地任意指定。如果指定流过元件的电流的参考方向是从标以电压正极性的一端指向负极性的一端，即两者的参考方向一致，则把电流和电压的这种参考方向称为关联参考方向；当两者不一致时，称为非关联参考方向。

下图中，a 和 b 是关联参考方向，c 是非关联参考方向。

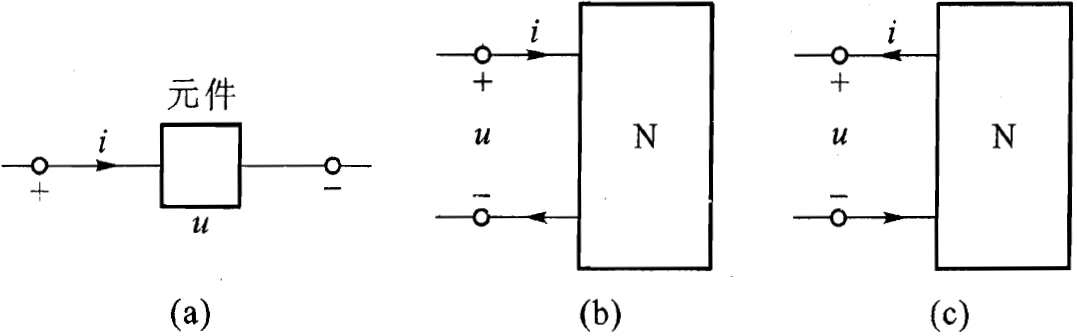
分析电路前必须选定电压和电流的参考方向。参考方向一经选定，必须在图中相应位置标注（包括方向和符号），在计算过程中不得任意改变。参考方向不同时，其表达式相差一负号，但电压、电流的实际方向不变。

关于电路中的做功：

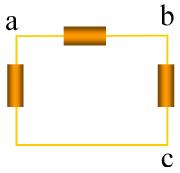
上图中，若单位正电荷从 a 到 b 电场力做功为 W1，单位正电荷从 b 到 c 电场力做功为 W2，则单位正电荷从 a 到 c 电场力做功为 W1+W2。做功可正可负，此处用代数值直接相加即可。

在国际单位制（SI）中，电流的单位为 A（安培，简称安），电荷的为单位为 C（库仑，简称库），电压的单位为 V（伏特，简称伏）。

1.3 电功率和能量

电路在工作状态下一定会发生电能和其他形式能量的转换。

电气设备、电路部件本身都有功率的限制，在使用时要注意其电流值或电压值是否超过额定值，过载会使设备或部件损坏，或是不能正常工作。

电功率与电压和电流密切相关。当正电荷从元件上电压的 "+" 极经元件运动到电压的 "-" 极时，与此电压相应的电场力要对电荷作正功，这时，元件吸收能量；反之，正电荷从电压的 "-" 极经元件运动到电压 "+" 极时，与此电压相应的电场力作负功，元件向外释放电能。

电场力做正功，元件吸收电能；电场力做负功，元件释放电能。

电功率即单位时间电场力所做的功。

如果在 dt 时间内，有 dq 电荷自元件上电压的 "+" 极经历电压 u 到达电压的 "-" 极，根据电压的定义（A、B 两点的电压 u 等于电场力将单位正电荷自 A 点移动至 B 点时所作的功），电场力所作功，也即元件吸收的的能量为

\[dW=udq \]

现在假设 i 在元件上与 u 成关联方向，由 i 的定义 i=dq/dt，有 dW= uidt，功率是能量的导数，故元件的吸收功率为：

\[p=\frac{dW}{dt} =ui \]

在 \(t_{0}\) 到 t 的时间内，元件吸收的能量为：

\[W(t)=\int dW=\int_{q(t_{0})}^{q(t)} udq=\int_{t_{0}}^{t} u(\xi )i(\xi )d\xi \]

由于 u、i 都是代数量，因此，功率 p 和吸收的能量 W 也都是代数量。当 p>0，W>0，元件确实吸收功率与能量；当 p<0，W<0 时，元件实际释放电能或发出功率。

当电流单位为 A，电压的单位为 V，时间的单位为 s（秒）时，能量的单位为 J（焦耳，简称焦），功率的单位为 W（瓦特，简称瓦）。

Watt 瓦特

Joule 焦耳

在指定电压和电流的参考方向后，应用式 \(p=ui\) 求功率 p 时应当注意：当电压和电流的参考方向为关联参考方向时，乘积 ui 表示元件吸收的功率；当 p 为正值时，表示该元件确实吸收功率。如果电压和电流的参考方向为非关联参考方向时，乘积 ui 表示元件发出的功率，此时，当 p 为正值时，该元件确实发出功率。

一个元件若吸收功率 100W，也可以认为它发出功率 -100W，同理，一个元件若发出功率 100W，也可以认为它吸收功率 -100W。这两种说法是一致的。

求功率的方法：先写出公式 ui，再在前面加两次正负号，第一次看 u 和 i 是否是关联参考方向，若是关联参考方向，则加 +，若是非关联参考方向，则加 -。再看若求的是吸收的功率，则加 +，若求的是释放的功率，则加 -。

全部按吸收的功率求解时，吸收的功率有正有负，正表示实际确实吸收功率，负表示实际是释放功率。此时全按吸收求出来的功率的和为零。全按释放的功率求解的结果之和也为零，原因同上。

恒定量的除法在变量中变为求导，是求导函数而不是求导函数在某一点的值。恒定量的乘法在变量中变为积分，且是求变上限积分。

求导函数和求变上限积分是对偶关系。

由于能量守恒，而功率是能量对时间的导数，则某一时刻的功率也守恒。

功率和能量的正负号一定是一致的，要么都是正，要么都是负。

1.4 电路元件

电路元件是电路中最基本的组成单元。电路元件通过其端子与外部连接。元件的特性通过与端子有关的电路物理量描述。每种元件通过端子的两种物理量反映一种确定的电磁性质。元件的两个端子的电路物理量之间的代数函数关系称为元件的端子特性（亦称元件特性）。集总（参数）元件假定：在任何时刻流入二端元件的一个端子的电流一定等于从另一端子流出的电流，且两个端子之间的电压为单值量。由集总元件构成的电路称为集总电路，或称具有集总参数的电路。用有限个集总元件及其组合模拟实际的部件和器件以及用集总电路作为实际电路的电路模型是有条件的。

集总参数电路和分布参数电路成对偶关系。

视为集中元件（电路）的条件：d <<λ

d 为电路或元件的尺寸。

λ 为电磁波的波长。

集总电路中的 u 和 i 可以是时间的函数，但是和空间坐标无关。即 u 和 i 可以和时间有关，但一定和空间无关。

电路物理量有电压 u、电流 i、电荷 q 以及磁通 \(\Phi\)（或磁通链 \(\Psi\)）等。电阻元件的元件特性是电压 u 与电流 i 的代数关系 u=f(i)；电容元件的元件特性是电荷 q 与电压 u 的代数关系 q=h(u)；电感元件的元件特性是磁通链 \(\Psi\) 与电流 i 的代数关系 \(\Psi=g(i)\)。

如果表征元件特性的代数关系是一个线性关系，则该元件称为线性元件。如果表征元件特性的代数关系是一个非线性关系，则该元件称为非线性元件。

电路元件按与外部连接的端子数目可分为二端、三端、四端元件等。电路元件还可分为线性元件和非线性元件，时不变元件和时变元件，无源元件和有源元件等。

集总参数（Lumped Parameter）元件是指有关电、磁场物理现象都由元件来 "集总" 表征。在元件外部不存在任何电场与磁场。如果元件外部有电场，进、出端子的电流就有可能不同；如果元件外部有磁场，两个端子之间的电压就可能不是单值的。

集总参数元件假定元件所发生的所有电磁过程全部集中在元件内部进行，在元件外部不存在任何电场和磁场。

1.5 电阻元件

线性电阻元件是这样的理想元件：在电压和电流取关联参考方向时，在任何时刻其两端的电压和电流服从欧姆定律：

\[u=Ri \]

R 为电阻元件的参数，称为元件的电阻。R 是一个正实常数。

当电压单位用 V，电流单位用 A 时，电阻的单位为 Ω（欧姆，简称欧）。

令 \(G=\frac{1}{R}\)，则有 \(i=Gu\)。

G 称为电阻元件的电导，单位是 S（西门子，简称西）。

R 和 G 都是电阻元件的参数。

电流和电压取非关联参考方向时，有 u=-Ri，i=-Gu。

欧姆定律只适用于线性电阻，即 R 和 G 都是常数。

欧姆定律说明线性电阻是无记忆的、双向性的元件。这一点区别于电感和电容。

Ohm：欧姆
Siemens：西门子

电阻可认为是对电流的阻碍，电导可认为是对电流的导通。R 越大则阻碍越大，则 G 越小，即导通能力越小。

由于电压和电流的单位是伏和安，因此电阻元件的特性称为伏安特性。

不存在阻值小于等于零的电阻。存在相当于阻值小于等于零的电阻的东西，比如电源。一个电路中有一个或多个电源，至少有一个电源的电流和电压取非关联参考方向，因为只有这样这个电源才是释放电能。对于非关联参考方向的电源，根据欧姆定律可知电阻为负。这里只是 "相当于"，因为欧姆定律不适用于电源。

线性电阻元件的伏安特性曲线是通过原点的一条线。直线的斜率与元件的电阻 R 有关。

电阻元件及其伏安特性曲线：

当一个线性电阻元件的端电压不论为何值时，流过它的电流恒为零值，就把它称为 "开路"。开路的伏安特性曲线在 u-i 平面上与电压轴重合，它相当于 R=∞ 或 G=0。当流过一个线性电阻元件的电流不论为何值时，它的端电压恒为零值，就把它称为 "短路"。短路的伏安特性曲线在 u-i 平面上与电流轴重合，它相当于 R=0 或 G=∞。如果电路中的一对端子之间呈断开状态，这相当于两个端子之间接有 R=∞ 的电阻，此时称两个端子处于 "开路"。如果把两个端子用理想导线（电阻为零）连接起来，称这对端子被短路。

开路和短路的伏安特性曲线：

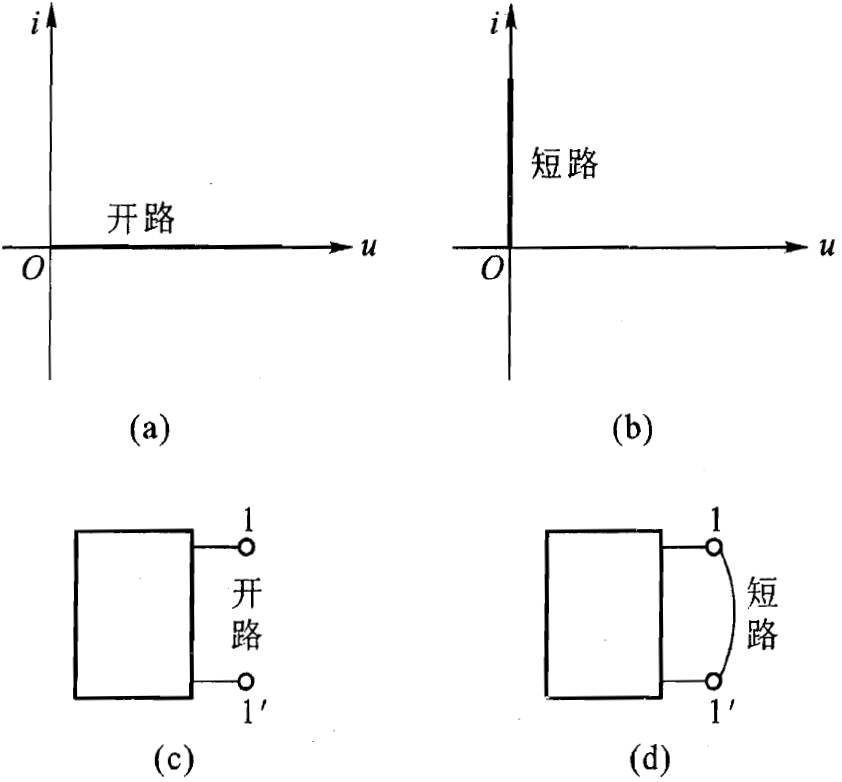
当电压 u 和电流 i 取关联参考方向时，电阻元件消耗的功率为：

\[p=ui=Ri^{2}=\frac{u^{2}}{R}=Gu^{2}=\frac{i^{2}}{G} \]

如果 u 和 i 为非关联参考方向，则电阻吸收的功率为 $p=-ui=(-)(-)Rii=Ri $，公式不变。

R 和 G 是正实常数，故功率 p 恒为非负值。所以线性电阻元件是一种无源元件。

电阻元件从 \(t_{0}\) 到 t 的时间内吸收的电能为：

\[W=\int_{t_{0}}^{t} Ri^{2}(\xi )d\xi \]

电阻元件一般把吸收的电能转换成热能或其他能量。

由于制作材料的电阻率与温度有关，（实际）电阻器通过电流后因发热会使温度改变，因此，严格说，电阻器带有非线性因素。但是在正常工作条件下，温度变化有限，许多实际部件如金属膜电阻器、线绕电阻器等，它们的伏安特性曲线近似为一条直线。所以用线性电阻元件作为它们的理想模型是合适的。

一点通识：通常情况，白炽灯温度升高则电阻上升，光敏电阻接受光照后电阻下降。

非线性电阻元件的伏安特性曲线不是一条通过原点的直线。非线性电阻元件的电压电流关系一般可写为 \(u=f(i)\) 或 \(i=h(u)\)。

如果一个电阻元件具有以下的电压电流关系：u(t)=R(t)i(t) 或 i(t)=G(t)u(t) 这里 u 与 i 仍是比例关系，但比例系数 R 是随时间变化的，故称为时变电阻元件。

线性电阻元件的伏安特性曲线位于第一、三象限。如果一个电阻元件的伏安特性曲线位于第二、四象限，则此元件的电阻为负值，即 R<0。负电阻元件实际上是一个发出电能的元件。如果要获得这种元件，一般需要专门设计。

今后，为了叙述方便，把线性电阻元件简称为电阻。

热量 \(Q=I^{2}Rt\)

表达式 \(\frac{U^{2}}{R}t\) 无意义。

对于线性电阻，能量全用来发热，则有 W=Q。

而线性电阻满足欧姆定律，即 U=IR，带入得 \(W=Q=\frac{U^{2}}{R}t\)，即便相等但表达式 \(\frac{U^{2}}{R}t\) 仍无物理意义。

对于其他元件，如电机，总功除了发热还有机械能。则 W>Q，则 \(UIt>I^{2}Rt\)，即 U>IR，也验证了不满足欧姆定律。

此时表达式 \(\frac{U^{2}}{R}t\) 无意义，即表达式 \(\frac{U^{2}}{R}t\) 是根据欧姆定律推出的，本身无意义，也只有在欧姆定律满足时才成立。

1.6 电压源和电流源

实际电源有电池、发电机、信号源等。电压源和电流源是从实际电源抽象得到的电路模型，它们是二端有源元件。理想电源无内阻。

理想电压源的定义：其两端电压总能保持定值或一定的时间函数，其值与流过它的电流i无关的元件叫理想电压源。

理想电压源简称为电压源，因为本书只考虑电路模型，而电路模型是由理想电路元件构成的。

电压源的端电压由元件本身决定，流过它的电流由其电压和外电路共同决定。

电压源是一个理想电路元件，它的端电压u(t)为 \(u(t)=u_{S}(t)\)。

式中 \(u_{S}(t)\) 为给定的时间函数，称为电压源的激励电压。电压源电压 u(t) 与通过元件的电流无关，总保持为给定的时间函数，而电流的大小则由外电路决定。

当 \(u_{S}(t)\) 为恒定值时，这种电压源称为恒定电压源或直流电压源，用 \(U_{S}\) 表示。

电压源的图形符号：

有时也可以用蓄电池的图形符号表示直流电压源，其中长线表示电源的 "+" 端：

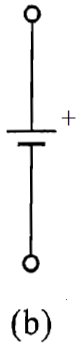
下图是电压源接外电路的情况：

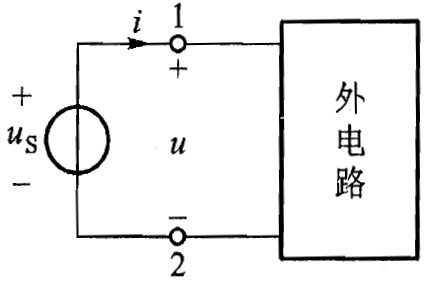
端子 1、2 之间的电压 u(t) 等于 \(u_{s}(t)\)，不受外电路的影响。

上图中，电压源的电压和通过电压源的电流的参考方向取为非关联参考方向，此时，电压源发出的功率为 \(p(t)=u_{s}(t)i(t)\)。这也是外电路吸收的功率。因为整个电路功率平衡。

电流（正电荷）从低电位运动到高电位，电场力做负功，电压源释放电能。

非关联参考方向要加一个负号，又因为求的是释放的功率，则需要再加一个负号，于是就相当于不加正负号。

下图示出电压源在 \(t_{1}\) 时刻的伏安特性曲线，它是一条不通过原点且与电流轴平行的直线。当 \(u_{s}(t)\) 随时间改变时，这条平行于电流轴的直线也将随之平移其位置。

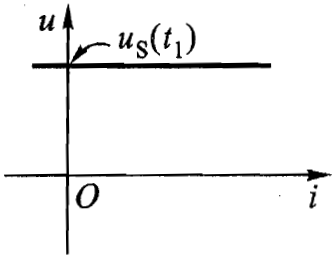
下图是直流电压源的伏安特性曲线，它不随时间改变。

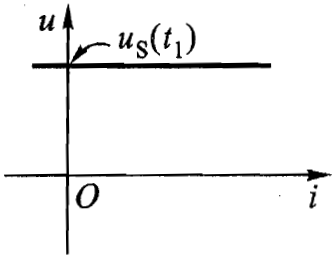
电压源不接外电路时，电流 i 总为零值，这种情况称为 "电压源处于开路"。如果一个电压源的电压 \(u_{s}=0\)，则此电压源的伏安特性曲线为 i-u 平面上的电流轴，它相当于短路。把 \(u_{s}≠0\) 的电压源短路是没有意义的，因为短路时端电压 u=0，这与电压源的特性不相容。

电压源不允许被短路。如果短路，因为导线没有电势差，导线是等势线，就要求电压源两端电势相等，显然不可能。

其输出电流总能保持定值或一定的时间函数，其值与它的两端电压 u 无关的元件叫理想电流源。

电流源是一个理想电路元件。电流源发出的电流 i(t) 为 \(i(t)=i_{S}(t)\)。\(i_{S}(t)\) 为给定时间函数，称为电流源的激励电流。因而电流源的电流与元件的端电压无关，并总保持为给定的时间函数。电流源的端电压由外电路决定。

电流源的电流由元件本身决定。电流源两端的电压由元件本身和外电路共同决定。

电流源的图形符号：

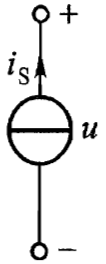
电流源接外电路的情况：

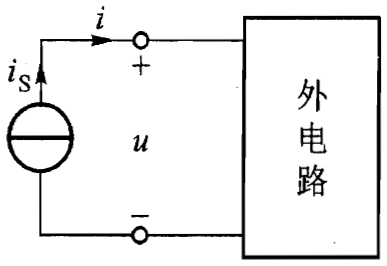
上图中，电流源电流和电压的参考方向为非关联参考方向，所以电流源发出的功率为 \(p(t)=u(t)i_{S}(t)\)。它也是外电路吸收的功率。

电流源在 \(t_{1}\) 时刻的伏安特性曲线：

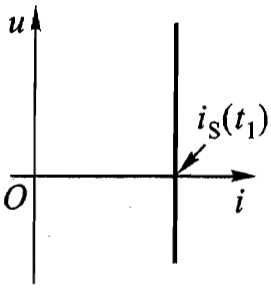
这是一条不通过原点且与电压轴平行的直线。当 \(i_{s}(t)\) 随时间改变时，这条平行于电压轴的直线将随之平移其位置。

下图示出直流电流源的伏安特性曲线，它不随时间改变。

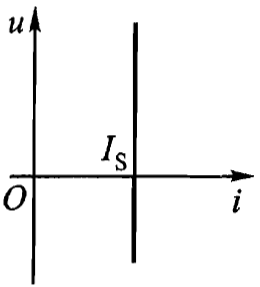
电流源两端短路时，其端电压 u=0，而 \(i=i_{S}\)，短路电流就是激励电流。如果一个电流源的 \(i_{S}=0\)，则此电流源的伏安特性曲线为 u-i 平面上的电压轴，它相当于开路。把 \(i_{S}\ne 0 的\) 电流源开路是没有意义的，因为开路时的电流 i 必须为零，这与电流源的特性不相容。

电流源不允许被开路。如果开路，从电流源出来的电流将无处可去。

电压源不允许短路。

电流源不允许开路。

当电压源的电压 \(u_{s}(t)\) 或电流源的电流 \(i_{s}(t)\) 随时间作正弦规律变化时，则称为正弦电压源或正弦电流源。以正弦电压源为例，有：

\[\begin{align} u_{s}(t)&=U_{m}cos(\frac{2\pi }{T} t + \phi ) \\ &=U_{m}cos({2\pi }{f} t + \phi )\\ &=U_{m}cos(\omega t + \phi ) \end{align} \]

式中 \(U_{m}\) 为正弦电压的最大值，T 为正弦函数的周期，f 为其频率，单位为 Hz（赫兹，简称赫），ω=2πf 为角频率，Φ 为正弦函数的初相角。正弦电压也可以用 sine 函数表示。

常见实际电源（如发电机、蓄电池等）的工作机理比较接近电压源，其电路模型是电压源与电阻的串联组合。像光电池一类器件，工作时的的特性比较接近电流源，其电路模型是电流源与电阻的并联组合。另外，专门设计的电子电路可作为电流源而广泛应用于集成电路之中。

光电池的采光极板接受一定的光通量时，在一定的电压范围内，其电流几乎不变。相当于一个电流源。

上述电压源和电流源常常被称为 "独立" 电源，"独立" 二字是相对于 "受控" 电源来说的。

实际电流源的产生：可由稳流电子设备产生，如晶体管的集电极电流与负载无关；光电池在一定光线照射下光电子被激发产生一定值的电流等。

电源的电压和电流为非关联参考方向时，电源释放能量，发出功率，起电源作用。电源的电压和电流为关联参考方向时，电源吸收能量，吸收功率，充当负载。此时电源没有得到充分利用。

通常，电源都是取非关联参考方向。

1.7 受控电源

受控（电）源又称 "非独立" 电源。受控电压源的激励电压或受控电流源的激励电流与独立电压源的激励电压或独立电流源的激励电流有所不同，后者是独立量，前者则受电路中某部分电压或电流控制。

电压或电流的大小和方向不是给定的时间函数，而是受电路中某个地方的电压（或电流）控制的电源，称受控源。

双极晶体管的集电极电流受基极电流控制，运算放大器的输出电压受输入电压控制，所以这类器件的电路模型中要用到受控源。

受控电压源或受控电流源视控制量是电压或电流可分为电压控制电压源（VCVS）、电压控制电流源（VCCS）、电流控制电压源（CCVS）和电流控制电流源（CCCS）。这 4 种受控源的图形符号如下图所示。

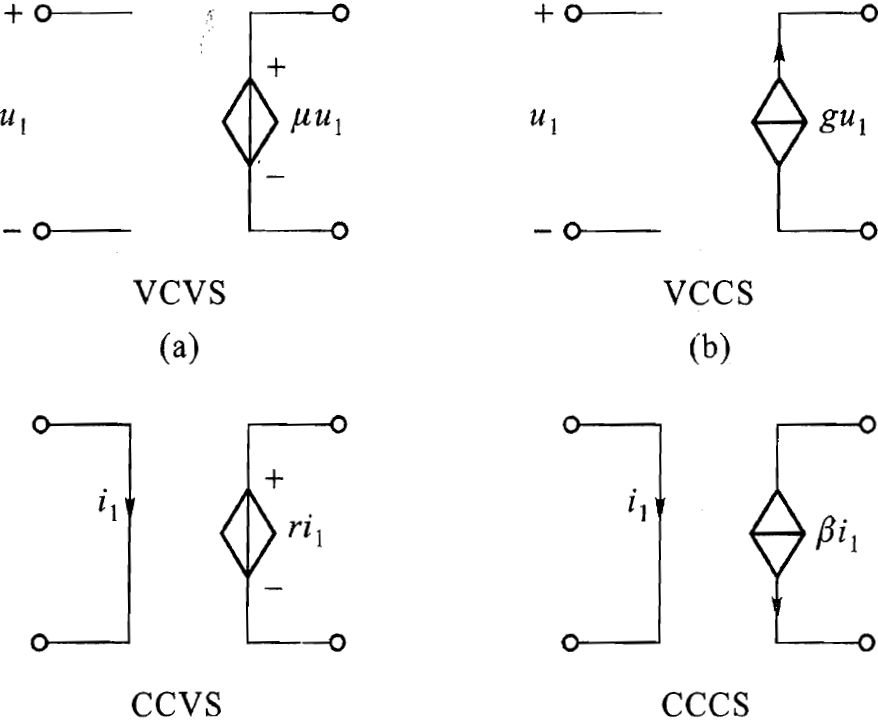
此处只是画得很近，但实际在电路里控制量和受控量可以离得很远。

控制量

受控量

控制端子

受控端子

上图中把受控源表示为具有 4 个端子的电路模型，其中受控电压源或受控电流源具有一对端子，另一对控制端子则或为开路，或为短路，分别对应于控制量是开路电压或短路电流。这样处理有时会带来方便。所以可以把受控源看作是一种四端元件，但在一般情况下，不一定要在图中专门标出控制量所在处的端子。

VCVS — Voltage Controlled Voltage Source

VCCS — Voltage Controlled Current Source

CCVS — Current Controlled Voltage Source

CCCS — Current Controlled Current Source

为了与独立电源相区别，用菱形符号表示其电源部分。图中 \(u_{1}\)、和 \(i_{1}\) 分别表示控制电压和控制电流，μ、r、g 和 β 分别是有关的控制系数，其中 μ 和 β 是量纲一的量，r 和 g 分别具有电阻和电导的量纲。这些系数为常数时，被控制量和控制量成正比，这种受控源称为线性受控源。

受控源的输入即控制部分，输出即受控部分。

μ：电压放大倍数。

g：转移电导。

r：转移电阻。

β：电流放大倍数。

受控源：受控电压源，受控电流源。

受控电压源：受控量是电压。

受控电流源：受控量是电流。

独立电源是电路中的 "输入"，它表示外界对电路的作用，电路中电压或电流是由于独立电源起的 "激励" 作用产生的。受控源则不同，它是用来反映电路中某处的电压或电流能控制另一处的电压或电流的现象，或表示一处的电路变量与另一处电路变量之间的一种耦合关系。在求解具有受控源的电路时，可以把受控电压（电流）源作为电压（电流）源处理，但必须注意其激励电压（电流）是取决于控制量的。

独立源在电路中起 "激励" 作用，在电路中产生电压、电流，而受控源是反映电路中某处的电压或电流对另一处的电压或电流的控制关系，在电路中不能作为 "激励"。

1.8 基尔霍夫定律

集总电路由集总元件相互连接而成。基尔霍夫定律是集总电路的基本定律。

把组成电路的每一个二端元件称为一条支路，把支路的连接点称为结点。

一个二端元件即一个支路，有多少个二端元件就有多少个支路。多个支路构成一个闭合路径则为一个回路。

路径：两结点之间的一条通路。由一条或多条支路构成。

回路是由支路构成的闭合路径。

回路只考虑个数，不必考虑方向。

网孔：对平面电路，其内部不含有任何支路的回路称为网孔。

如果将电路中各个支路的电流和支路的电压（简称支路电流与支路电压）作为变量来看，这些变量受到两类约束。一类是元件的特性造成的约束。例如，线性电阻元件的电压与电流必须满足 u=Ri 的关系。这种关系称为元件的组成关系或电压电流关系（VCR - Voltage Current Relation），即 VCR 构成了变量的元件约束。另一类约束是由于元件的相互连接给支路电流之间或支路电压之间带来的约束关系，有时称为 "几何" 约束或 "拓扑" 约束，这类约束由基尔霍夫定律来体现。

元件约束是元件自身的电流电压约束，基尔霍夫定律是元件之间连接引起的支路电流和支路电压之间的约束。

基尔霍夫定律与元件特性一起构成了电路分析的基础。

基尔霍夫定律包括电流定律和电压定律。

基尔霍夫电流定律（KCL - Kirchhoff's Current Law）指出："在集总电路中，任何时刻，对任一结点，所有流出结点的支路电流的代数和恒等于零"。

此处，电流的 "代数和" 是根据电流是流出结点还是流入结点判断的。若流出结点的电流前面取 "+" 号，则流入结点的电流前面取 "-" 号；电流是流出结点还是流入结点，均根据电流的参考方向判断。

所以对任一结点有 KCL 两种定义方式：

（1）第一种定义方式：

\[\sum i=0 \]

上式取和是对连接于该结点的所有支路电流进行的。

（2）第二种定义方式：

\[\sum i_{入}=\sum i_{出} \]

方法一列出来的式子的 i 前面有正有负，方法二列出来的式子的 i 前面全是正号。

在代入 i 的具体值时由于 i 是代数量又会引入正负号。

因此，KCL 也可理解为，任何时刻，流出任一结点的支路电流等于流入该结点的支路电流。

KCL 通常用于结点，但对包围几个结点的闭合面也是适用的。

通过一个闭合面的支路电流的代数和总是等于零；或者说，流出闭合面的电流等于流入同一闭合面的电流。这称为电流连续性。KCL 是电荷守恒和电流连续性原理在电路中任意结点处的反映。

KCL 是对结点处支路电流加的约束，与支路上接的是什么元件无关，与电路是线性还是非线性无关。

对于下图，应用基尔霍夫定律时，有多少个元件就有多少个支路，所以这里有 5 条支路。另一种定义支路的方法是电路中通过同一电流的分支，即多个元件若电流一样则为同一支路。这样定义的话这里有 3 条支路。这两种定义分别用在不同的地方。

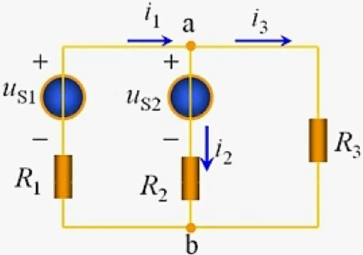
该图有回路 3 个，网孔 2 个。

对应两种支路的定义方法，结点也有两种定义方法。对应于第一种支路定义，可以定义元件的连接点为结点，于是这张图中的最上面和最下面两条线分别视为一个结点，两个电压源和电阻之间各自有一个结点，共 4 个结点。对应于第二种支路定义，可以定义结点为三条支路的连接点。

基尔霍夫电压定律（KVL - Kirchhoff's Voltage Law） 指出："在集总电路中，任何时刻，沿任一回路，所有支路电压的代数和恒等于零"。

定义 KVL 的两种方法：

（1）第一种方法：

\[\sum u=0 \]

（2）第二种方法：

\[\sum u_{降}=\sum u_{升} \]

上式取和时，需要任意指定一个回路的绕行方向，凡支路电压的参考方向与回路的绕行方向一致者，该电压前面取 "+" 号，支路电压参考方向与回路绕行方向相反者，前面取 "-" 号。

不管哪种方法，第一步都是想象出一个回路，并指明回路的方向。第一种方法中，把回路方向假想为电流方向，若电压的参考方向和这个方向为参考方向，则取正号，为非关联参考方向则取负号。

方法一列出来的式子的 u 前面有正有负，方法二列出来的式子的 u 前面全是正号，在代入 u 的具体值时由于 u 是代数量又会引入正负号。

KVL 是对回路中的支路电压加的约束，与回路各支路上接的是什么元件无关，与电路是线性还是非线性无关。KVL 方程是按电压参考方向列写，与电压实际方向无关。

KVL 和 KCL 的方法一对应。KVL 和 KCL 的方法二对应。

KVL 可适用于任一假想回路，尤其是回路本身断开时将其假想为闭合。

KVL 的实质反映了电路遵守能量守恒定律。KVL 是电压与路径无关这一性质的反映。实质上，也是能量守恒和转换定律的反映。

KCL 在支路电流之间施加线性约束关系；KVL 则对支路电压施加线性约束关系。这两个定律仅与元件的相互连接有关，而与元件的性质无关。不论元件是线性的还是非线性的，时变的还是时不变的，KCL 和 KVL 总是成立的。KCL 和 KVL 是集总电路的两个公设。

对一个电路应用 KCL 和 KVL 时，应对各结点和支路编号，并指定有关回路的绕行方向，同时指定各支路电流和支路电压的参考方向，一般两者取关联参考方向。

例题：

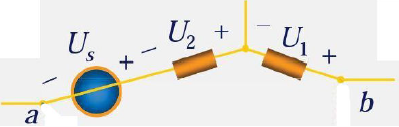
假想 a 点和 b 点之间有电压，由图可以看出 b 到 a 一直是降压，故 b 点电压高于 a 点，设电压为 \(U_{ba}\)，则有：\(U_{ba}=U_{1}+U_{2}+U_{s}\)。