代码随想录Day15_二叉树

1.平衡二叉树

题目理解：

左子树和右子树的高度差不超过1。
求左子树高度，求右子树高度，如果差1或者0就返回true.至于高度.
不能用求最大深度做,因为最大深度中高度的相加是通过最后1+max() 实现的.

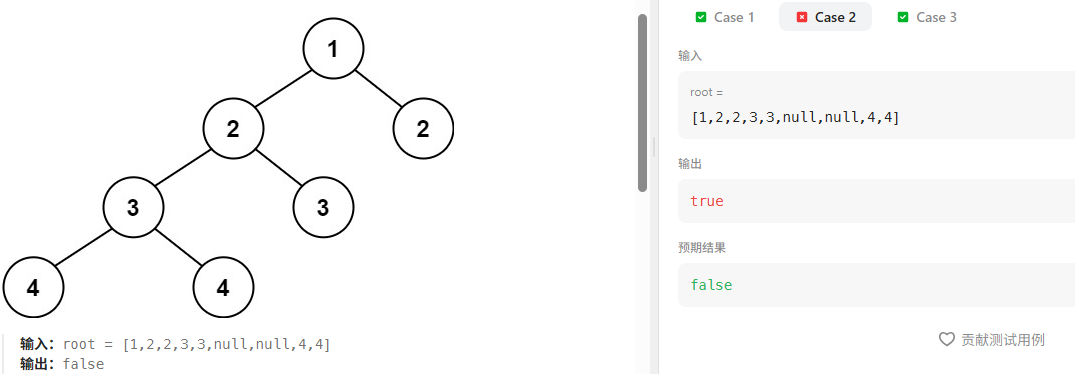
题目理解错了，平衡二叉树，说的是所有节点的左子树和右子树的高度差，并非是根节点。在看对称二叉树时，判断的是根节点的左右子树的情况。因此参数一定是节点。

题目思路

不懂为什么要引出高度和深度以及遍历方式？
先三部曲：
1.参数是节点，返回值是高度，int;
2.终止条件：节点空
3.单层循环的逻辑：左右子树的差值。

代码实现

class Solution {
public:
    bool isBalanced(TreeNode* root) {
        return GetHi(root)==-1? false:true;
    }
    int GetHi(TreeNode* node){
        if(node==NULL)   return 0;
        int leftH = GetHi(node->left);
        int rightH = GetHi(node->right);
        if(leftH == -1)  return -1;
        if(rightH == -1)  return -1;
        return abs(rightH-leftH)>1? -1:1+max(rightH,leftH);
    }

2.二叉树的所有路径

题目理解

根节点到叶子经过的所有节点。

思路

对于一个节点，要是有左节点，就输出来，要是有右节点就输出来，直到没有左节点，也没有右节点。用动态数组存。

代码

class Solution {
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<int>path;
        vector<string>result;
        if(root ==NULL) return result;
        Tranverse(root,path,result);
        return result;
    }
private:
    void Tranverse(TreeNode* node,vector<int>&path,vector<string> &result){
        path.push_back(node->val);
        if(node->left==NULL&&node->right==NULL){
            string spath;
        for(int i=0;i<path.size()-1;i++){
            spath += to_string(path[i]); 
            spath +="->";
        }
        spath+=to_string(path[path.size()-1]);
        result.push_back(spath);
        //return ;
        }
        if(node->left){
            Tranverse(node->left,path,result);
            path.pop_back();
        }
        if(node->right){
            Tranverse(node->right,path,result);
            path.pop_back();
        }
    }
};

3.左叶子之和

题目理解

是左叶子！是没有孩子的节点，不是左节点！
叶子节点：如果已经遍历到了叶子节点，那么就不知道它是否是左节点，因此参数是叶子节点的上一个节点。

思路

1.参数 TreeNode node 返回值 int;
2.终止条件：root==NULL;
3.单层循环：遇见左叶子，记录左叶子；

• 递归求左子树叶子和；
• 递归求右子树叶子和；
• 返回和。

代码

class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        return tranverse(root);
    }
    int tranverse(TreeNode* node){
        if(node == NULL) return 0;
        int leftNum =tranverse(node->left);
        if(node->left!=0&&node->left->left==NULL&&node->left->right==NULL)
        leftNum+=node->left->val;//左
        int rightNum =tranverse(node->right);//右
        int sum =leftNum+rightNum;//中
        return sum;
    }
    
};

3.完全二叉树节点的数量

题目理解

思路

这个递归真是完全不理解，为什么要确定一个终止条件后还要再写一个判断满二叉树，满二叉树是为了简化。

代码

class Solution {
public:
    int countNodes(TreeNode* root) { return GetNum(root); }
private:
    int GetNum(TreeNode* node) {
        if (node == NULL)
            return 0;
        int leftDepth = 0;
        int rightDepth = 0;
        TreeNode* LeftNode=node->left;
        while (LeftNode) {
            LeftNode = LeftNode->left;
            leftDepth++;
        }
        TreeNode* RightNode = node->right;
        while (RightNode) {
            RightNode = RightNode->right;
            rightDepth++;
        }
        if(leftDepth == rightDepth) {return (2<<leftDepth)-1;}
        int leftNum = GetNum(node->left);
        int rightNum = GetNum(node->right);
        int sum = leftNum + rightNum+1;
        return sum;
    }
};