[No0000100]正则表达式匹配解析过程分析(正则表达式匹配原理)&regexbuddy使用&正则优化
常见正则表达式引擎
引擎决定了正则表达式匹配方法及内部搜索过程,了解它至关重要的。目前主要流行引擎有:DFA,NFA两种引擎。
|
引擎 |
区别点 |
|
DFA |
DFA引擎它们不要求回溯(并因此它们永远不测试相同的字符两次),所以匹配速度快!DFA引擎还可以匹配最长的可能的字符串。 不过DFA引擎只包含有限的状态,所以它不能匹配具有反向引用的模式,还不可以捕获子表达式。 代表性有:awk,egrep,flex,lex,MySQL,Procmail |
|
NFA 非确定型有穷自动机 又分为传统NFA,Posix NFA |
传统的NFA引擎运行所谓的“贪婪的”匹配回溯算法(longest-leftmost), 以指定顺序测试正则表达式的所有可能的扩展并接受第一个匹配项。 传统的NFA回溯可以访问完全相同的状态多次,在最坏情况下,它的执行速度可能非常慢,但它支持子匹配。 代表性有:GNU Emacs,Java,ergp,less,more,.NET语言 ,PCRE library,Perl,PHP,Python,Ruby,sed,vi等, 一般高级语言都采用该模式。 |
DFA以字符串字符为主,逐个在正则表达式匹配查找,而NFA以正则表达式为主,在字符串中逐一查找。尽管速度慢,但是对操作者来说更简单,因此应用更广泛!下面所有以NFA引擎举例说明,解析过程!
解析引擎眼中的字符串组成
对于字符串“DEF”而言,包括D、E、F三个字符和 0、1、2、3 四个数字位置(零宽空间):0D1E2F3,对于正则表达式而言所有源字符串,都有字符和位置。正则表达式会从0号位置(可以匹配^),逐个去匹配的。
占有字符和零宽度
正则表达式匹配过程中,如果子表达式匹配到的是字符内容,而非位置,并被保存到最终的匹配结果中,那么就认为这个子表达式是占有字符的(IsMatch开始为true);如果子表达式匹配的仅仅是位置,或者匹配的内容并不保存到最终的匹配结果中,那么就认为这个子表达式是零宽度的(IsMatch不为true)。占有字符是互斥的,零宽度是非互斥的。也就是一个字符,同一时间只能由一个子表达式匹配,而一个位置,却可以同时由多个零宽度的子表达式匹配。常见零宽字符有:^,(?=)等
正则表达式匹配过程详解实例
我们掌握了上面几个概念,我们接下来分析下几个常见的解析过程。结合使用软件regexBuddy来分析。
regexbuddy正则表达式测试工具使用方法(图文)
1、安装完regexbuddy
该工具支持多种程序语言正则表达式,如:perl,pcre,javascript,python,ruby,c#,java等等,还能自动生成程序代码,并且内部带有大量的常用正则表达式。
2、一般切换到side by side:
3、匹配过程
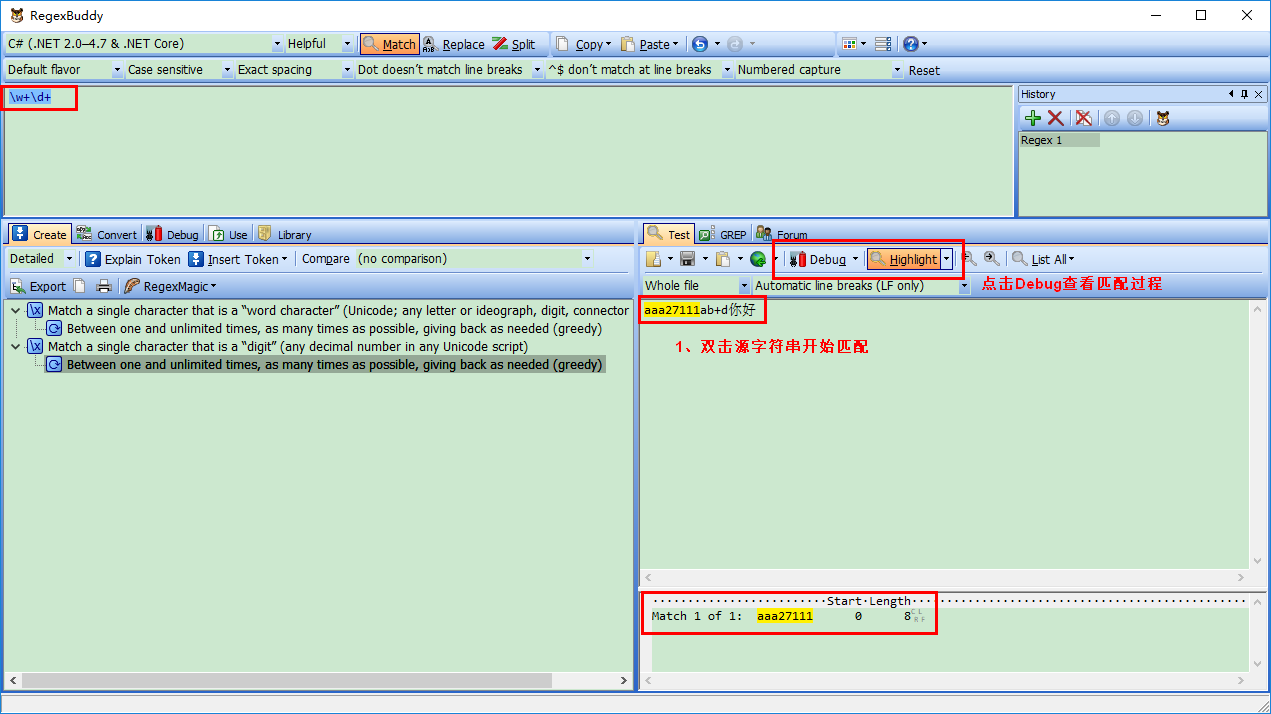
匹配完,点击“Test”里面Debug(Here),自动切换到Debug界面:
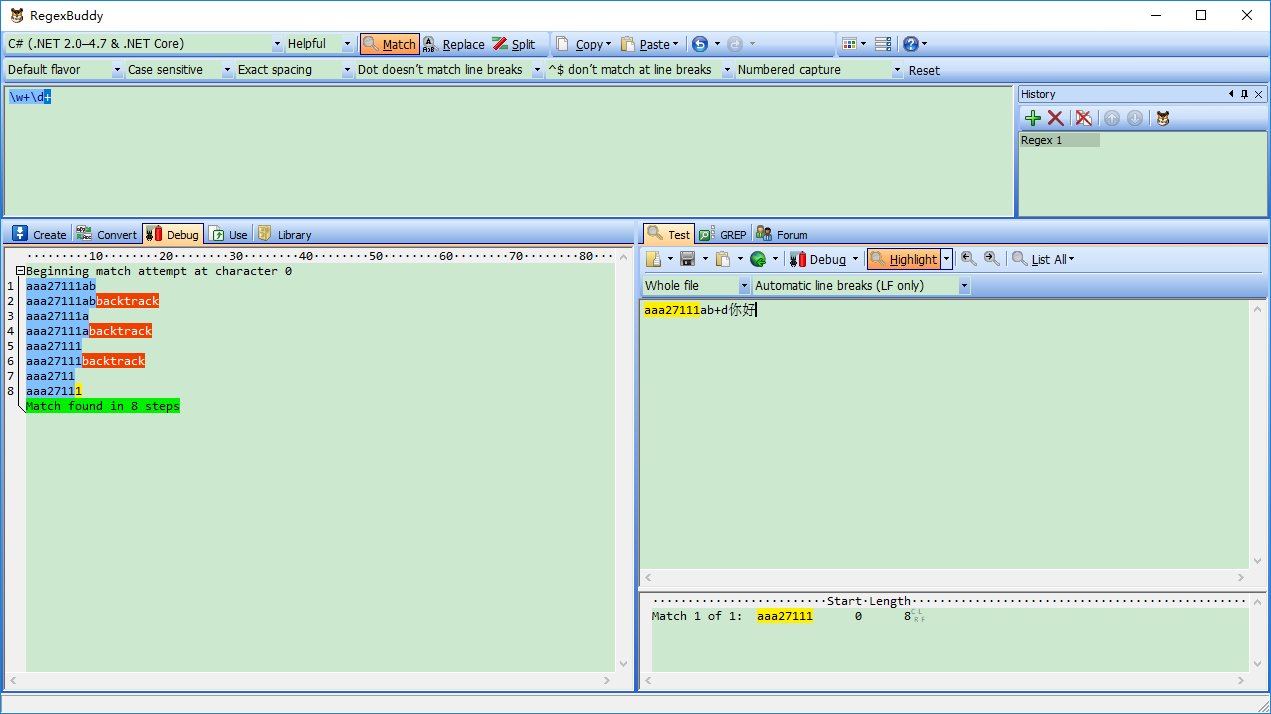
匹配过程:\w+一下子贪婪匹配aaa27111ab,然后\d+没有匹配字符串了。开始回逆了,逐个字符减少,直到发现最后一个字符“1”与\d+匹配为止。最终匹配到字符串是:“aaa27111”
从上面一个匹配看,这个简单一个匹配,搜索了8次,进行了不断查找。如果我们已经准确知道自己要匹配什么样字符,我们可以对源正则表达式修改下,减少匹配次数。就达到优化正则表达式目的,提高匹配效率!
如果我们知道源字符串只是a-z字符,进行修改发现,只要用2次搜索就匹配到所需字符。
为什么需要性能测试工具
我们都知道,正则表达式使用进行搜索查找,没有字符串直接查找快!而且性能是几何倍数下降。那么,为什么正则表达式速度会比字符串搜索慢呢。我们来看看,正则表达式查找字符串的匹配过程吧。正则表达式由一些元字符,普通字符,量词字符组合成。默认情况下,这些量词元字符(*,+,?)都是贪婪模式,会最大长度匹配字符串。我们知道,正则表达式往往搜索路径会有多个,我们看看,下面匹配过程。就知道,主要影响正则表达式执行性能有哪些了。
正则表达式匹配过程如:\d+abc,元字符是:”12345bdc”,查找会从左向右进行,\d+,贪婪模式,一下子匹配到12345,然后bdc与\d+不能匹配,”abc”中,”a”字符,开始匹配”bdc”,发现匹配失败。正则表达式开始回溯匹配(贪婪模式量词开始逐一减少匹配字符长度),\d+只匹配”1234”,”5bdc”与”abc”匹配,任然失败。\d+继续减少匹配长度为:”123”,”45bdc”与”abc”匹配,任然失败。继续回退,直到\d+匹配”1”,用”2345bdc”与”bdc”匹配,任然失败。整个匹配就失败了。
从上面过程中,我们发现,每次回溯,要重新操作匹配因此匹配搜索次数,直接影响正则表达式的性能。做正则表达式性能优化,一般就是优化查询的次数。这个是我们分析过程,如果有个工具能够实实在在看到每一步匹配过程,对于我们优化正则表达式将带来太多方便了。这里介绍工具是:regexbuddy软件,它就是一个实实在在看到匹配过程工具。
Demo1: 源字符DEF,对应标记是:0D1E2F3,匹配正则表达式是:“DEF”
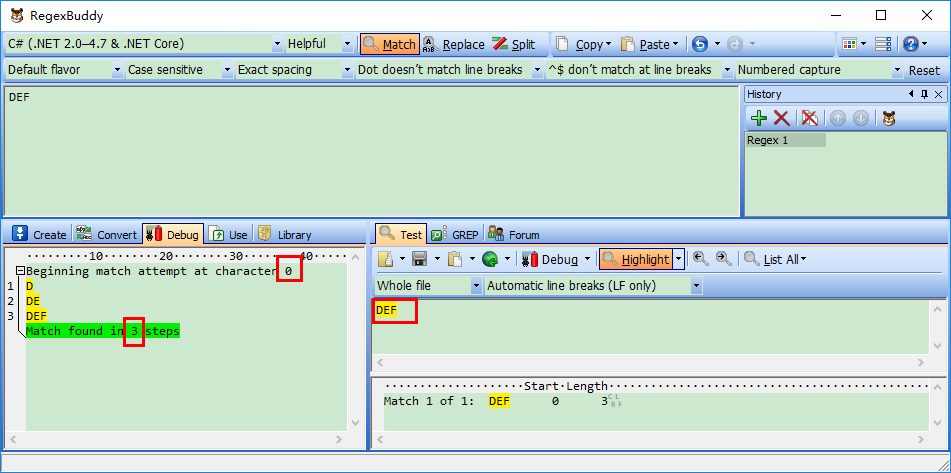
过程可以理解为:首先由正则表达式字符 “D” 取得控制权,从位置0开始匹配,由 “D” 来匹配“D”,匹配成功,控制权交给字符 “E” ;由于“D”已被 “D” 匹配,所以 “E” 从位置1开始尝试匹配,由“E” 来匹配“E”,匹配成功,控制权交给 “F”;由“F”来匹配“F”,匹配成功。
Demo2:源字符DEF,对应标记是:0D1E2F3,匹配正则表达式是:/D\w+F/

过程可以理解为:首先由正则表达式字符 /D/ 取得控制权,从位置0开始匹配,由 /D/ 来匹配“D”,匹配成功,控制权交给字符 /\w+/ ;由于“D”已被 /D/ 匹配,所以 /\w+/ 从位置1开始尝试匹配,\w+贪婪模式,会记录一个备选状态,默认会匹配最长字符,直接匹配到EF,并且匹配成功,当前位置3了。并且把控制权交给 /F/ ;由 /F/ 匹配失败,\w+匹配会回溯一位,当前位置变成2。并把控制权交个/F/,由/F/匹配字符F成功。因此\w+这里匹配E字符,匹配完成!
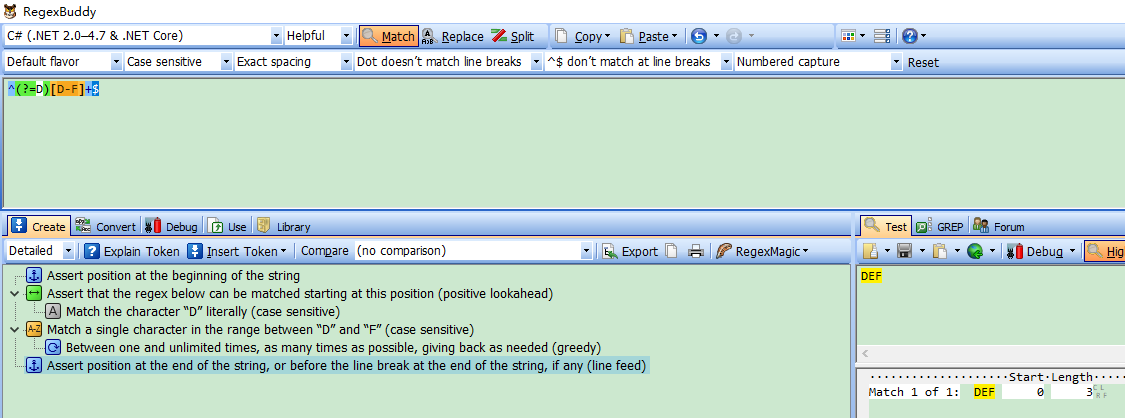
Demo3:源字符DEF,对应标记是:0D1E2F3,匹配正则表达式是:/^(?=D)[D-F]+$/
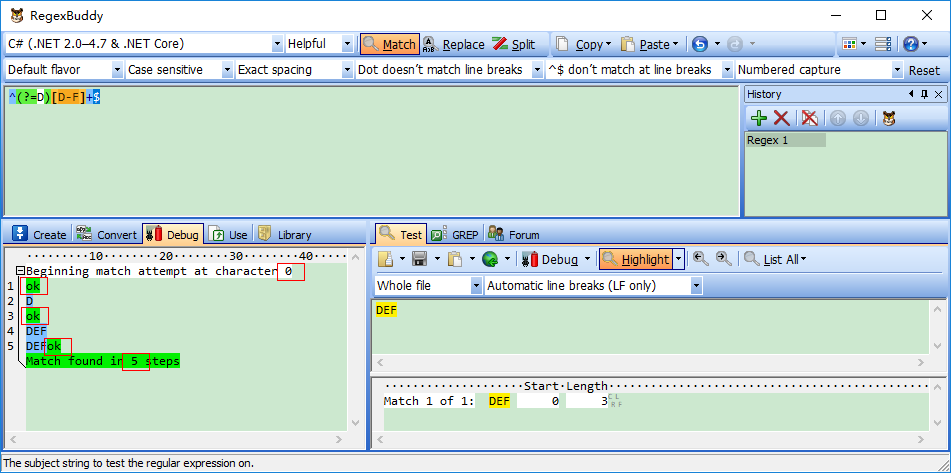
过程可以理解为:元字符 /^/ 和 /$/ 匹配的只是位置,顺序环视(匹配完开头,从左往右依次匹配) /(?=D)/ (匹配当前位置,右边是否有字符“D”字符出现)只进行匹配,并不占有字符,也不将匹配的内容保存到最终的匹配结果,所以都是零宽度的。 首先由元字符 /^/ 取得控制权,从位置0开始匹配, /^/ 匹配的就是开始位置“位置0”,匹配成功,控制权交给顺序环视 /(?=D)/;/(?=D])/ 要求它所在位置右侧必须是字母”D”才能匹配成功,零宽度的子表达式之间是不互斥的,即同一个位置可以同时由多个零宽度子表达式匹配,所以它也是从位置0尝试进行匹配,位置0的右侧是字符“D”,符合要求,匹配成功,控制权交给 /[D-F]+/ ;因为 /(?=D)/ 只进行匹配,并不将匹配到的内容保存到最后结果,并且 /(?=D)/ 匹配成功的位置是位置0,所以 /[D-F]+/ 也是从位置0开始尝试匹配的, /[D-F]+/ 首先尝试匹配“D”,匹配成功,继续尝试匹配,直到匹配完”EF”,这时已经匹配到位置3,位置3的右侧已没有字符,这时会把控制权交给 /$/,元字符 /$/ 从位置3开始尝试匹配,它匹配的是结束位置,也就是“位置3”,匹配成功。此时正则表达式匹配完成,报告匹配成功。匹配结果为“DEF”,开始位置为0,结束位置为3。其中 /^/ 匹配位置0, /(?=D)/ 匹配位置0, /[D-F]+/ 匹配字符串“DEF”, /$/ 匹配位置3。
匹配详解
- 用“(\$)”匹配“$1.30”
匹配结果:
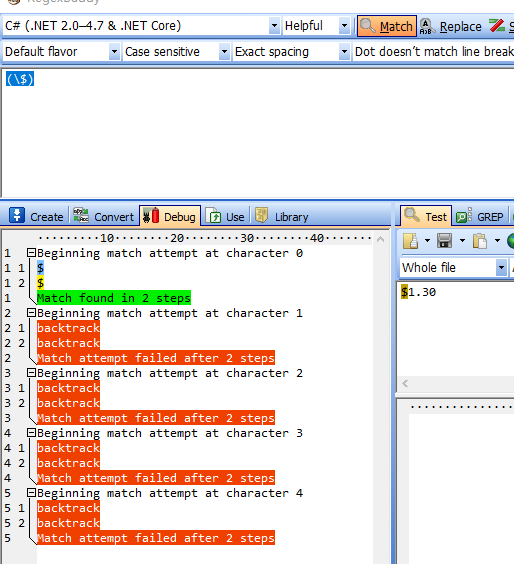
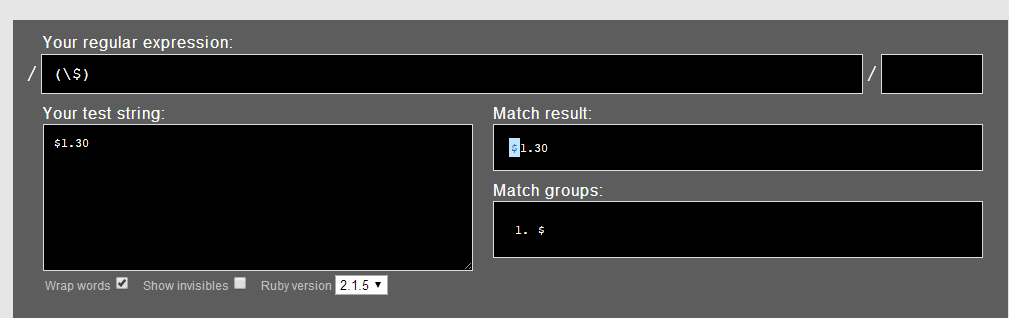
1.1.尝试从“ $ 1 . 3 0 ”的第一个“零宽空间”开始匹配“(\$)”: “ $ 1 . 3 0 ”匹配到,IsMatch=true。
1.2. 尝试从“ $ 1 . 3 0 ”的第二个“零宽空间”开始匹配“(\$)”:“1 . 3 0 ”依次均不匹配。
2. 用“(\$*)”匹配“$1.30”
匹配结果:
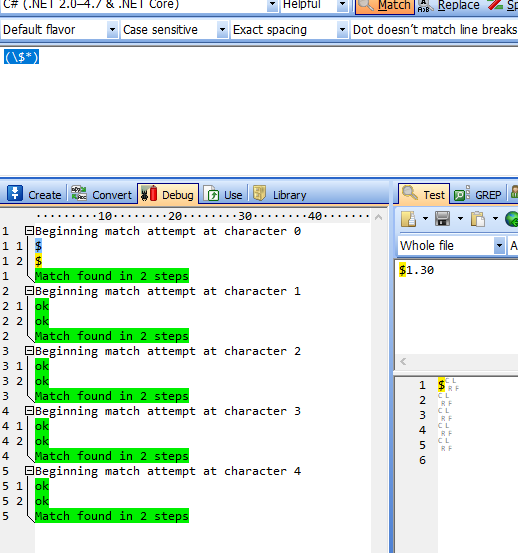

2.1.尝试从“ $ 1 . 3 0 ”的第一个“零宽位”开始匹配“(\$*)”: “ $ 1 . 3 0 ”匹配。(\$*是尽可能多的匹配$,此处匹配了1次$)
2.2尝试从“ $ 1 . 3 0 ”的第二个“零宽位”开始匹配“(\$*)”:由于1符合\$*(\$*是尽可能多的匹配$,此处匹配了0次$),所以“ 1”中的零宽空间被捕获,但1未被捕获。
2.3尝试从“ $ 1 . 3 0 ”的第三个“零宽位”开始匹配“(\$*)”:由于.符合\$*(\$*是尽可能多的匹配$,此处匹配了0次$),所以“ .”中的零宽空间被捕获,但.未被捕获。
2.4尝试从“ $ 1 . 3 0 ”的第四个“零宽位”开始匹配“(\$*)”:由于3符合\$*(\$*是尽可能多的匹配$,此处匹配了0次$),所以“ 3”中的零宽空间被捕获,但3未被捕获。
2.5尝试从“ $ 1 . 3 0 ”的第五个“零宽位”开始匹配“(\$*)”:由于0符合\$*(\$*是尽可能多的匹配$,此处匹配了0次$),所以“ 0”中的零宽空间被捕获,但0未被捕获。
2.6尝试从“ $ 1 . 3 0 ”的第六个“零宽位”开始匹配“(\$*)”:由于$(结尾)符合\$*(\$*是尽可能多的匹配$,此处匹配了0次$),所以“ $”(结尾)中的零宽空间被捕获,但结尾未被捕获。
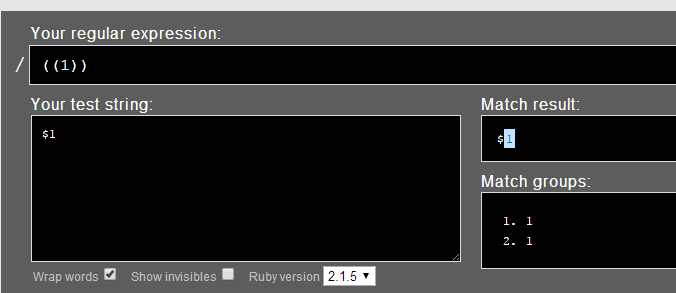
3. 用“((1))”匹配“$1”
匹配结果:

正则表达式,将数据库字段转换为驼峰式
使用:_([\W]) 查找
使用:\U\1\E 替换

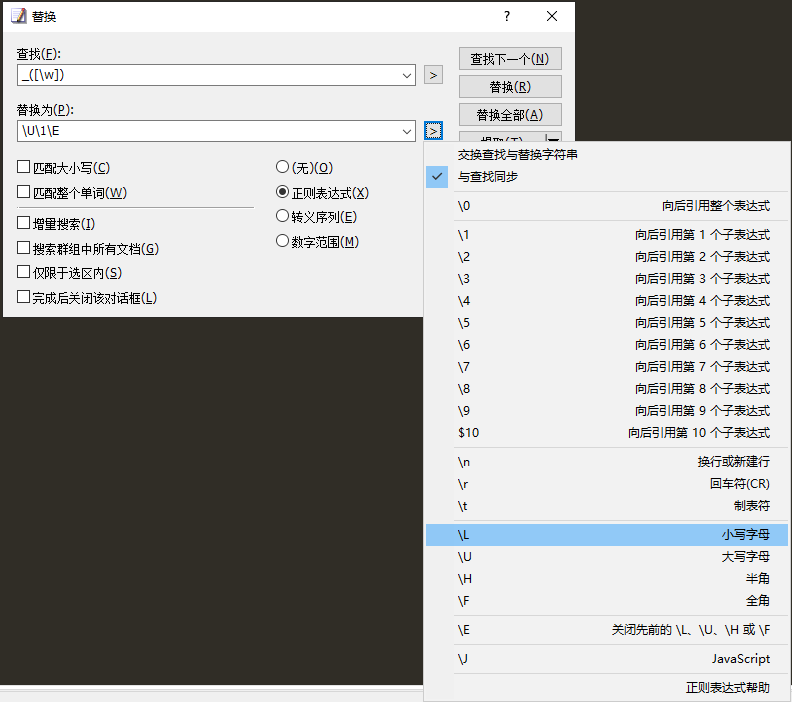
|
\L |
强制所有后续替换字符要小写。 |
|
\U |
强制所有后续替换字符要大写。 |
|
\H |
强制所有后续替换字符要是半角字符。 |
|
\F |
强制所有后续替换字符要是全角字符。 |
|
\E |
关闭之前的 \L,\U,\F 或 \H。 |
为部分替换表达式的扩展。
参见:http://www.emeditor.org/zh-cn/howto_search_replacement_expression_syntax.html;
正则表达式匹配原理
本文不会介绍正则表达式的语法,重点介绍正则表达式匹配原理,算法实现。相信大家也都知道正则表达式应用强大之处,这里也不再介绍其应用范围。
1. 正则引擎
我们可以将前面KMP算法,看作一台由模式字符串构造的能够扫描文本的有限状态自动机。对于正则表达式,我们要将这个思想推而广之。
KMP的有限状态自动机会根据文本中的字符改变自身的状态。当且仅当自动机达到停止状态时它找到一个匹配。算法本身就是模拟这种自动机,这种自动机的运行很容易模拟的原因是因为它是确定性的:每种状态的转换都完全由文本中的字符所确定。
而正则表达式需要一种更加抽象的自动机(引擎),非确定有限状态自动机(NFA)。正则引擎大体上可分为不同的两类:DFA和NFA,而NFA又基本上可以分为传统型NFA和POSIX NFA。
DFA–Deterministic finite automaton 确定型有穷自动机
NFA–Non-deterministic finite automaton 非确定型有穷自动机
- Traditional NFA
- POSIX NFA
2. 引擎区别
- DFA:
DFA 引擎在线性时状态下执行,因为它们不要求回溯(并因此它们永远不测试相同的字符两次)。DFA 引擎还可以确保匹配最长的可能的字符串。但是,因为 DFA 引擎只包含有限的状态,所以它不能匹配具有反向引用的模式;并且因为它不构造显示扩展,所以它不可以捕获子表达式。
- NFA:
传统的 NFA 引擎运行所谓的“贪婪的”匹配回溯算法,以指定顺序测试正则表达式的所有可能的扩展并接受第一个匹配项。因为传统的 NFA 构造正则表达式的特定扩展以获得成功的匹配,所以它可以捕获子表达式匹配和匹配的反向引用。但是,因为传统的 NFA 回溯,所以它可以访问完全相同的状态多次(如果通过不同的路径到达该状态)。
因此,在最坏情况下,它的执行速度可能非常慢。因为传统的 NFA 接受它找到的第一个匹配,所以它还可能会导致其他(可能更长)匹配未被发现。
NFA最重要的部分:回溯(backtracking)。回溯就像是在道路的每个分岔口留下一小堆面包屑。如果走了死路,就可以照原路返回,直到遇见面包屑标示的尚未尝试过的道路。如果那条路也走不通,你可以继续返回,找到下一堆面包屑,如此重复,直到找到出路,或者走完所有没有尝试过的路。
- POSIX NFA:
POSIX NFA 引擎与传统的 NFA 引擎类似,不同的一点在于:在它们可以确保已找到了可能的最长的匹配之前,它们将继续回溯。因此,POSIX NFA 引擎的速度慢于传统的 NFA 引擎;并且在使用 POSIX NFA 时,您恐怕不会愿意在更改回溯搜索的顺序的情况下来支持较短的匹配搜索,而非较长的匹配搜索。
DFA与NFA对比:
- DFA对于文本串里的每一个字符只需扫描一次,比较快,但特性较少。
NFA要翻来覆去吃字符、吐字符,速度慢,但是特性丰富,所以反而应用广泛。
当今主要的正则表达式引擎,如Perl、Ruby、Python的re模块、Java和.NET的regex库,都是NFA的。
- 只有NFA支持lazy、backtracking、backreference,NFA缺省应用greedy模式,NFA可能会陷入递归险境导致性能极差。
DFA只包含有穷状态,匹对相配过程中无法捕获子表达式(分组)的匹对相配结果,因此也无法支持backreference。
DFA不能支持捕获括号和反向引用。
POSIX NFA会继续尝试backtracking,以试图像DFA相同找到最长左子正则式。因此POSIX NFA速度更慢。
-
NFA是最左子式匹配,而DFA是最长左子式匹配。
-
NFA的编译过程通常要快一些,需要的内存也更少一些。
对于“正常”情况下的简单文本匹配测试,两种引擎的速度差不多。一般来说,DFA的速度与正则表达式无关,而NFA中两者直接相关。
- 对正则表达式依赖性较量强的操作系统(大量应用正则做搜索匹对相配),最好完全把握NFA->DFA算法,充分理解所应用的正则表达式引擎的思想和特性。
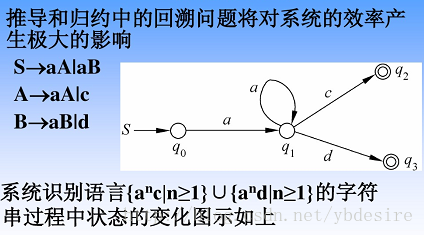
3. 匹配过程
首先构造NFA,如下图:

它是一个有向图,边表示了引擎匹配时的运行轨迹。从起始状态0开始,到达1的位置(也就是“((”后),它有两种选择,可以走2,也可以走6,…直到最后的接受状态。
得到有向图后,匹配实现就简单多了。这里用到了有向图的多点可达性问题–DirectedDFS算法。
-
首先我们查找所有从状态0通过ε-转换可达的顶点(状态)来初始化集合。对于集合的每个顶点,检查它是否可能与第一个输入字符相匹配。检查之后,就得到了NFA在匹配第一个字符之后可能到达的其他顶点。这里还需要向该集合中加入所有从该集合中的任意状态通过ε-转换可以到达的顶点。
-
有了这个匹配第一个字符之后可能到达的所有顶点的集合,ε-转换有向图中的多点可达性问题的答案就是可能匹配第二个输入字符的顶点集合。
-
重复这个过程直到文本结束,得到两种结果:最后的集合含有可接受的顶点;不含有。
注释,什么是ε-转换。

4. NFA的构造
将正则表达式转化为NFA的过程在某种程度上类似于Dijkstra的双栈算法对表达式求值的过程。
构造规则:

逻辑很容易理解,请参考如下代码和轨迹图:


5. 代码实现
附上DirectedDFS和Digraph类.
public class NFA { private Digraph graph; // digraph of epsilon transitions private String regexp; // regular expression private int m; // number of characters in regular expression /** * Initializes the NFA from the specified regular expression. * * @param regexp the regular expression */ public NFA(String regexp) { this.regexp = regexp; m = regexp.length(); Stack<Integer> ops = new Stack<Integer>(); graph = new Digraph(m+1); for (int i = 0; i < m; i++) { int lp = i; if (regexp.charAt(i) == '(' || regexp.charAt(i) == '|') { ops.push(i); } else if (regexp.charAt(i) == ')') { int or = ops.pop(); // 2-way or operator if (regexp.charAt(or) == '|') { lp = ops.pop(); graph.addEdge(lp, or+1); graph.addEdge(or, i); } else if (regexp.charAt(or) == '(') { lp = or; } else assert false; } // closure operator (uses 1-character lookahead) if (i < m-1 && regexp.charAt(i+1) == '*') { graph.addEdge(lp, i+1); graph.addEdge(i+1, lp); } if (regexp.charAt(i) == '(' || regexp.charAt(i) == '*' || regexp.charAt(i) == ')') { graph.addEdge(i, i+1); } } if (ops.size() != 0) { throw new IllegalArgumentException("Invalid regular expression"); } } /** * Returns true if the text is matched by the regular expression. * * @param txt the text * @return {@code true} if the text is matched by the regular expression, * {@code false} otherwise */ public boolean recognizes(String txt) { DirectedDFS dfs = new DirectedDFS(graph, 0); Bag<Integer> pc = new Bag<Integer>(); for (int v = 0; v < graph.V(); v++) { if (dfs.marked(v)) pc.add(v); } // Compute possible NFA states for txt[i+1] for (int i = 0; i < txt.length(); i++) { if (txt.charAt(i) == '*' || txt.charAt(i) == '|' || txt.charAt(i) == '(' || txt.charAt(i) == ')') { throw new IllegalArgumentException("text contains the metacharacter '" + txt.charAt(i) + "'"); } Bag<Integer> match = new Bag<Integer>(); for (int v : pc) { if (v == m) { continue; } if ((regexp.charAt(v) == txt.charAt(i)) || regexp.charAt(v) == '.') { match.add(v+1); } } dfs = new DirectedDFS(graph, match); pc = new Bag<Integer>(); for (int v = 0; v < graph.V(); v++) { if (dfs.marked(v)) pc.add(v); } // optimization if no states reachable if (pc.size() == 0) { return false; } } // check for accept state for (int v : pc) { if (v == m) return true; } return false; } /** * Unit tests the {@code NFA} data type. * * @param args the command-line arguments */ public static void main(String[] args) { String regexp = "(" + "(A*B|AC)D" + ")"; String txt = "AABD"; NFA nfa = new NFA(regexp); System.out.println(nfa.recognizes(txt)); } }
详解正则表达式匹配算法原理
注意:关于正则表达式的规则,网上内容已经很多了。所以本文不讲述正则表达式的规则,只讲其背后的算法原理。
1. 引入
正则表达式,Regular Expression,使用单个字符串来描述、匹配一系列满足某种句法规则的字符串。
在很多文本编辑器里,正则表达式通常被用来检索、替换那些匹配某个模式的文本。
最常见的,比如“.”,其中“.”表示匹配除“\n”之外的任何单个字符,“”表示匹配前面的子表达式零次或多次。
在python中,正则表达式的使用也很简单:
import re
regexObject = re.compile(r".*abc.*", flags=0) # 匹配含有abc的字符串
s1 = 'asd abc sd abc'
s2 = 'sdfsabcsdffa'
s3 = 'fsadf'
match1 = re.search(regexObject, s1) # <_sre.SRE_Match at 0x66473d8>
match2 = re.search(regexObject, s2) # <_sre.SRE_Match at 0x6647b90>
match3 = re.search(regexObject, s3) # None但是,正则表达式的内部原理是怎么样的呢? 它是按照什么算法来进行字符串匹配? 这就是本文要解释的内容。
2. 状态机
2.1 有限状态系统
下面直接给出几个有限状态系统的实例,从直观上就能理解有限状态系统:
- 例1:指针式钟表,一共有12*60*60个状态,每过一秒,钟表就从一种状态转换到另一种状态
- 例2:围棋共有3**361个状态,每走一步棋,就从一个状态转换到另一个状态
- 例3:语言的识别
2.2 有限状态机
有限状态机(英语:finite-state machine,缩写:FSM)又称有限状态自动机,简称状态机,是表示有限个状态以及在这些状态之间的转移和动作等行为的数学模型。
有些地方也叫“自动机”,指的都是同一个东西。
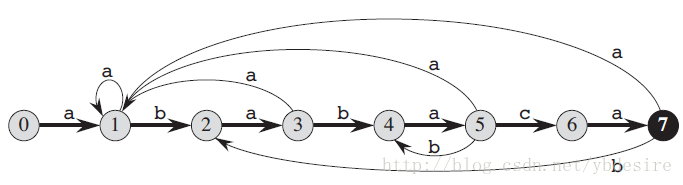
FSM的表示,我们常用状态转移图。下图就是一个模式字符串的FSM状态转移图:
给定待匹配的字符串”abababaca”,就能通过模式串的FSM进行匹配,这就是正则表达式的匹配思想。
3. 正则表达式匹配实例
给定正则表达式a(bb)+a,其中+表示匹配前面的子表达式一次或多次,所以字符串abba或abbbba都能被这个模式所匹配。
下图是该正则表达式对应的FSM状态转移图。
该FSM中,圈代表不同的状态。读入字符串时,就从一个状态进入另一个状态。FSM有开始和匹配(匹配)两种特殊状态,分别位于头部和尾部。
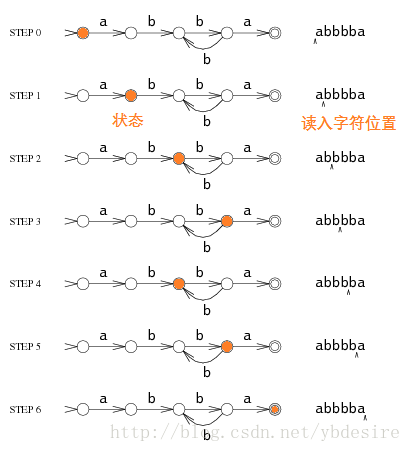
下面是匹配的过程示例图:
该状态机结束于最后一个状态,这是一个匹配成功的状态。若状态机结束于非匹配成功状态,那么匹配失败。如果在运行过程中,没有办法到达其他状态,那么状态机提前结束。
4. 多路径匹配
正则表达式等效于有限状态机,每一个正则表达式都有一个对应的有限状态机。反之,有限状态机也对应一个正则表达式。具体的对应关系可以参见这篇文章(https://sine-x.com/regexp-1/)。
下面是多路径的算法匹配过程:
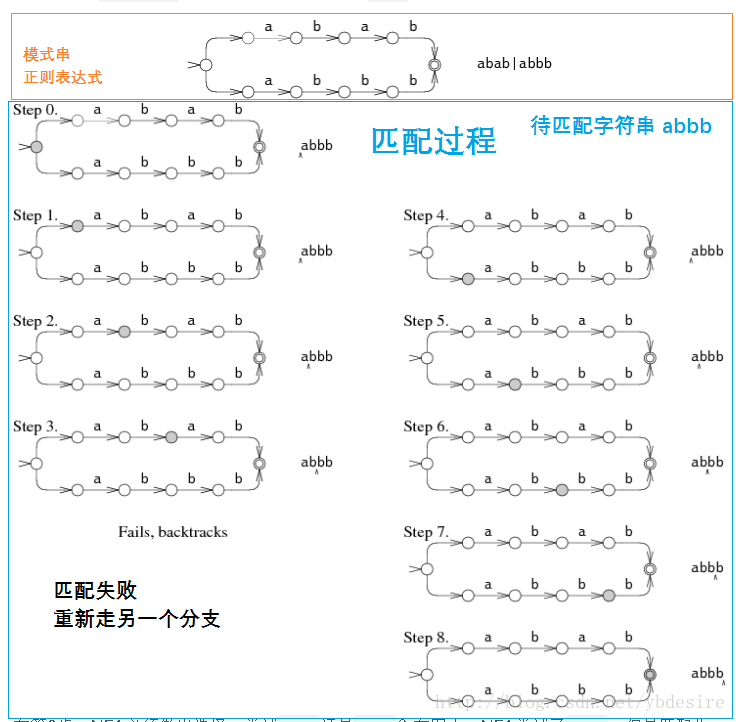
匹配时,可能有多条路径,遇到分支时,可以采用试错法,一条走不通,再尝试另一条。但这种做法效率较低。
所以另一种更优的做法,是在分支处同时匹配多条分支,同时保持多个状态,这样避免了很多不必要的尝试。
参考
本文中的图是直接从下文中截取出来再编辑的,在此感谢原图作者!


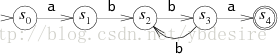

 浙公网安备 33010602011771号
浙公网安备 33010602011771号