一直迷糊的浮点数
之前写了 进制转换,也写了计算机怎么 存整数,那么问题来了,计算机中小数怎么存呢?比如2019.725怎么放到计算机里呢?-2019.725又该怎么办呢?
我们有什么
首先想一下我们有什么,计算机怎么存数。假如我们的计算机是存 32 位的,那么它就长下边的样子。

由于我们写数字,习惯于先写高位,所以把最低位画到了最右边。
我们需要做的就是把0和1放到上边的方框中,来表示2019.725。换言之,我们就是需要制定一个规则,把2019.725转成01字符串存进去。然后读取的时候,再把01字符串转成2019.725显示出来。
思路一
简单粗暴些,我们人为的把32个位置分成三部分,最高位0表示正数,1表示负数,然后是整数部分,再然后是小数部分。

低 10 位存小数部分,接下来的 21 位存整数部分,最高 1位存符号位。所以我们只需要把2019和725分别转成二进制,放进去就可以了。二进制位数不足的,高位补零就可以。
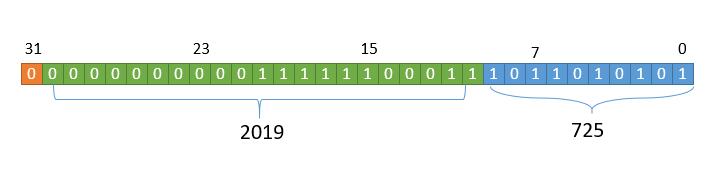
仔细想想,规则还不够完善,如果存10.3和10.03,小数部分怎么存呢?肯定不能都存3,这样两个数就不能区分了。这里我想到两种方案:
倒序
小数部分我们逆转以后去存,10.3小数部分存3,10.03小数部分存30。
补零
我们的小数部分是10个比特位,所以最多存 210210 个数,十进制的话就是0 - 1023。为了方便,把1000以上的数省略掉,范围变成000-999,也就意味着我们能精确的表示小数点后三位的数,如果一个数小数位数不足3位,我们就用零补齐。
10.3的话,可以看成10.300,小数部分存300,10.03的话可以看成10.030,小数部分就存30。
能表示的数字范围
整数部分我们有21个比特位,能表示的数是 221221 个,十进制的话就是 0 - 2097152。
小数部分如果用的倒序方案,那么我们的范围就是0 - 1023。
综上,数字范围就是 -2097152.1023 ~ 2097152.1023。
应用
MySQL 中的定点数DECIMAL就是采取的上边的思想,将整数部分和小数部分分别存储。不同之处是MySQL采用了变字长存储,根据十进制的大小,利用不同的字节去存储,所以理论上它能存的范围是无限的。
详细的介绍可以参考 你可能不知道的MySQL中的定点数类型。
思路二
上边的方案有一个问题,表示的数字的范围有些小,最大也才两百多万。限制范围的原因就是,上边的方案整数部分只用了21个比特位去存。
换一种思路,我们通过移动小数点把小数转成整数,然后再记录小数点移动的位数。
我们用3个比特位来记录移动的位数,这样我们就可以把小数点移动7位。此外,整数部分就可以有28个比特位来表示了,范围大大增加。

其实可以看做是科学计数法的形式,比如2019.725,可以看做是 2019725×10−32019725×10−3,我们只需要把 2019725和指数3存起来就可以了。

能表示的数字范围
28个比特位来表示整数部分,能表示的数的个数就是 228228,对应的十进制范围就是0 - 268435455。
又因为最多可以移动 7 位的小数,所以数字范围就是下边的
-268435455.0000000 ~ 268435455.0000000。
可以看到比之前的方案扩大了两个数量级,精度也提高了。但是我们要意识到一件事情,两种方案都用了32个比特位,所以最多就是表示 232232 个数。思路二表示的范围虽然扩大了,并不是这个范围内的所有数都能精确表示,能表示的数的范围是0 - 268435455,也就是能表示的有效数字最多只有九位。
对于思路一的最大数2097152.1023,如果用思路二,虽然它在-268435455.0000000 ~ 268435455.0000000之内,但是由于它的有效数字位数是11位,但我们最多存储9位的,所以我们只好把小数点后的最后两位舍去,存储2097152.10。
应用
对于C#中的System.Decimal是用的类似于思路二的思想,具体的话参考 没有神话,聊聊decimal的“障眼法”。
思路三
上边的思路一和思路二都是站在十进制数的角度上先考虑对数字的分割、转换,然后将十进制的整数转为二进制进行存储的。再换一种思路,先把十进数转成二进制数,再去存呗。
对于2019.725转成二进制就是11111100011.1011100110...,为啥出现了省略号?进制转换中已经讨论过这个问题了,那就是大部分十进制数并不能精确的转到二进制,这是一个固有的事实,我们也没啥办法,假装没有省略号,继续讨论吧。
尾数部分
这里存储的话,可以借鉴思路二,我们可以把二进制小数转换成科学计数法的形式,统一规格再去存储。这里用个小技巧,我们知道所有的数字除了0之外,一定会含有一个1,所以我们把数字转成下边的形式。
为什么要用上边的形式呢,这样做的一个好处就是存的时候,我们只需要存xxxxxxxxx...的部分,显示数字的时候再考虑它的最高位还有一个1。这样如果用23个比特位来存数字,相等于存储了24位。
指数
区别于思路二的指数,思路二我们是把原来的小数转为整数,所以指数一定是个负数,直接存它的绝对值就行。但在这里如果之前的数字是 0.000001这样的,那么指数E是负数,但如果是1110011.1这样的,指数E就是正数了。
如果指数E是用8个比特位来存储,那么总共就是 2828 个数,范围就是0 - 255,那么怎么存负数呢?最简单的方案,人为规定呗,将一部分正数映射到负数上,就对半分吧。
1
|
0 1 125 126 127 128 129 254 255
|
要表示的指数加上127映射到0 - 255。反过来显示指数真正值的时候,需要减去127。
综上所述,我们就用 1 个比特位来存符号位,8个比特位来存指数,存的时候记得加上偏移,剩下的23个比特位来存有效数字,而事实上我们其实可以看做存了24位。

这样的话,求出2019.725的二进制是 11111100011.1011100110011。把它规格化,小数点需要向左移动10位,也就代表指数是 10,存的话还需要加上127,也就是137了,二进制表示是10001001。所以规格化就是下边的数了:
所以计算机中就是下边这样存的了。

特殊数字
我们还有个问题没有解决,上边规格化的时候我们默认了所有数字至少有一个1,但是0怎么办呢?规则是我们自己定的,继续定呗。
当指数是-127时,一个很小很小的数了,此时对应的指数加上127,也就是0。我们规定当E为0并且M全为0,我们就说这个数字是0。
-127用了以后,负指数最小就是-126了。
让我们再规定几个特殊的数字。
当指数是128时,一个很大很大的数,也就是当 E 全为1。分几种情况。
-
有效数字
M每一位全为0,-
S为0,就代表正无穷。 -
S为1,就代表负无穷。
-
-
有效数字 M 每一位不全为 0,代表
NaN,表示不是一个数字。
所以此时正指数最大就是127了。
能表示数的范围
最大数和最小数
最大的数,指数最大取1111 1110,也就是254,减去127,代表指数是127。有效数字全部取1,也就是1.111...1,小数点后边23个1。然后把它转成十进制的话,用一个技巧,先给它加 2−232−23,这样所有的1都产生进位,变成了10.0000000,这样的话转成十进制就是2了,当然我们还要减去 2−232−23。
综上,最大的数字用十进制表示就是 (2−2−23)×2127(2−2−23)×2127,也就是 3.4028234663852886×10383.4028234663852886×1038。
所以能表示的范围就是 −3.4028234663852886×1038−3.4028234663852886×1038 到 3.4028234663852886×10383.4028234663852886×1038。
再看一下能表示的最小正数。指数取最小为 0000 0001,减去127,代表指数是-126。有效数字全部取0,其实也就代表1.000...0000,总共有23个0,转成十进制的话就是1×2−1261×2−126,也就是 1.1754943508222875×10−381.1754943508222875×10−38。
有没有发现一个问题,我们要找最小的数,但因为之前的规定,最高位却能是1。但理论上我们找一个0.000...1这样的数才代表最小的正数。怎么得到这样的数呢?
再加个规则吧。当时我们规定当E为0的并且M每一位全为0,我们就说这个数字是0。那M不全为零呢?
之前是假设省略了最高位1,我们加一个新规则,当E全为0时,我们就说最高位不再省略1。所以最小的尾数就可以是0.00...1了,小数点后22个零,转成十进制就是 2−232−23。指数还是之前的-126,所以比之前更小的正数就是 2−23×2−126=2−1492−23×2−126=2−149,也就是 1.401298464324817×10−451.401298464324817×10−45。
精度
我们用23个比特位表示尾数部分,最多能表示 223223 个数,也就是8388607,从十进制的角度,所以它的有效数字最多有7位。
应用
上边介绍的其实就是IEEE 754标准了,计算机中存储32位浮点数基本上都是这个规则。比如java中的float类型,可以看一下jdk源码中的一些定义。
1
|
/**
|
可以看到float的最大值,和正数的两个最小值和我们分析的完全一致。
当然,上边的我们分析的是32位的情况,64位的话和32位基本是一样的,对应于java中的double类型。

除了位数变多以外,其它的分析和32位都是一样的,此时指数不再加127,而是加1023。
一些问题
1
|
0.1 + 0.2 == 0.3 //false
|
这样就可以理解上边的经典问题了,之所以两边不相等,第一个原因就是大部分十进制并不能精确的转为二进制,第二个原因就是存储的位数有限,会进行一些舍去。
如果对于一些能精确表示的浮点数,判断相等就不会出问题了。
1
|
0.125 + 0.125 == 0.25 //true
|
另一个问题,当我定义一个变量
1
|
float a = 0.1;
|
既然不能精确表示0.1,那么我们把它输出的时候为什么显示的是0.1。
在 进制转换 中我们算过,0.1 转成二进制的话是0.0 0011 0011 0011...,因为我们只能存23位有效数字,所以我们只能存0.000 1 1001 1001 1001 1001 1001 101。
因为我们最高位可以省略个 1,所以就是第一个1后边有23位。
此外,最后 3 位本来是100,因为100后边一位是1,所以相当于产生进位变成101。
这个二进制数还原为10进制的话就是0.10000000149011612。
让我们来验证一下
1
|
System.out.println(String.format("%.18f", 0.1f));
|
和我们预想的完全一样,而如果不加限制直接输出0.1,显示0.1只是因为默认的有效位数比较少,其实只是输出了近似值0.1。
结束
浮点数的探究到此结束了,回顾一下,前两种方法我们先从十进制的角度来考虑,通过存整数来存小数,从而保证了我们可以精确存数。思路三,我们先把十进制转成二进制去存,这就产生了不能精确的存储数的问题。同时有两个技巧也值得注意,第一个就是用存储指数的时候,我们用正数表示负数。第二个就是,默认规定最高位是1,从而用23个比特位存了24位的数据。
理解进制转换的原理
准备写一篇关于浮点数存储的,然后先写了进制转换,越写越多,就单独作为一篇文章吧。
2019.723,这个数的二进制形式是什么样呢?让我们慢慢考虑。
数字的概念
首先思考一下数字是什么?为什么要有数字。
我有一个苹果,你脑海中会出现一个苹果。
我有五个苹果,你脑海中会出现五个苹果。
我有三十个苹果,你脑海中会出现三十个苹果。
我有一千个苹果,你可能想象不出来了。
数字的作用,就是让我们对一个东西的数量有一个更精确的认识。如果没有数字,我可能只能说我有一桌子苹果,我有一堆苹果,我有一大堆苹果,我有一大大堆苹果,这些都是感性的认知,每个人的认知可能是不一样的,而数字统一了我们对「量」的概念。
此外,另一个神奇的地方在于数字仅仅是「量」的概念,他没有限制去描述什么。
比如说五个苹果,五只小狗,五头牛,五粒大米,数量都是五,但他们的体积、质量、形状都和他们本身有关了。
数字的记录
后来人类发明了纸笔,如果把这个「量」的概念写下来该怎么办呢?
最简单的想法就是画竖线,每增加一个,就加一条竖线。
1 -> I
2 -> II
3 -> III
4 -> IIII
5 -> IIIII
20 -> ???
如果数字大了,一直画竖线显然是不现实的,在出土的甲骨文中发现了当时人们对数字的认识。
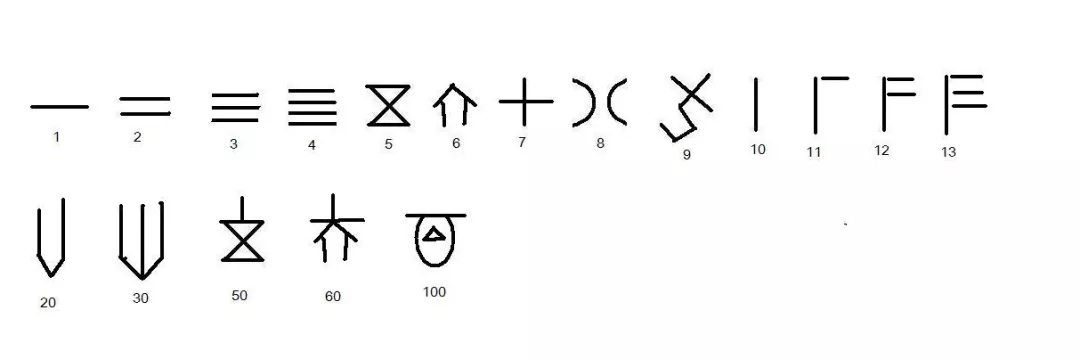
一些大的数字用一些特定的符号来表示,这样如果表示 108 的话,我们只需要画出这两个图形就可以了。
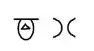
顺序无所谓,另一个人可能画出的是下边的
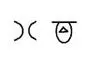
即使顺序不一样,但他们表示的数字都是 108。
进制的概念
上边的依旧不是很方便,比如我要是想表示 1000,如果我们只有 100 对应的符号,我还是需要画 10 个才行。接下来,人们用了一个更伟大的发明,进位制,也许因为人有 10 根手指,所以采用了 10 进制,其实就是我们现在的计数法。用0 - 9 十个符号就可以表示任意数字了。
这里边最伟大的发明就是0的概念了,它除了表示数量上的 0,也可以用来占位。从而数字在不同的位置有了不同的含义。拿十进制来举例,就是逢十进一。
得到一个苹果,写个 1,得到六个苹果,写个6,得到十个苹果了,怎么表达十这个数量呢,低位用0占位,高位写1就可以了。也就是10。此时的1不再是一,而是一个十。同理100,就表明有十个十的数量。此外再发明一个小数点,0.1,小数点右边的一表明是十分之一。
每个位置就有了不同的含义,可以看作下边的公式。e 是小数点后开始的数位。
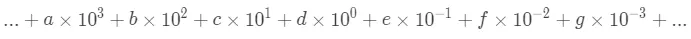
a,b,c … 代表0 - 9中的任意一个符号,现在的数量是a个1000,b 个 100,c 个 10……
比如2019.723就可以看成下边的样子
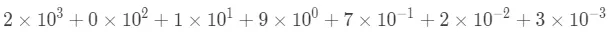
上边是十进制,让我们想一下 2 进制。
2 进制只有两个符号可以用,那就是0和 1,规则是满2 就要进 1。
如果有一个苹果那么就记做1,如果有两个苹果要利用0来占位,高位写1,也就是10,如果有四个苹果,那就用100来表示。
因为我们对十进制太熟悉了,如果我说「我考了100分」。大家第一反应就是我考的不错,但如果是在二进制的世界,100其实是一个蛮小的数字。
如果把二进制换两个符号,比如>来表示一个苹果,<来表示零的概念,用来占位。我如果说我考了><<分,这样大家就没有条件反射觉得我考的很高了。
所以我们要明确一个概念,不同进制下,可能用了同一个符号,但对于同一个数量,那么表示法是不一样的。

看到这么多苹果,
商朝人可能会写下,我有| 二个苹果。
十进制的人们会写下,我有 12 个苹果。
二进制的人们会写下,我有 1100 个苹果。
可以看到对于同一个数量,大家的表示是不一样的,即使十进制和二进制的人们用了相同的符号0和1,但由于进制不同,他们写出来是不一样的。
有一天二进制的人和十进制的人相遇了,二进制的人说,我买了1100个苹果,然后对于十进制的人第一反应,哇,一千多个苹果,也太多了吧。
二进制的人们,看到1100立马脑海中联想到了上图的数量,但是对于十进制人们必须把这个数量转换成自己熟悉的十进制表示,才可以在脑海里想象1100个苹果的数量是多少。那么怎么转换呢?
二进制转十进制
让我们从十进制的角度去看一下二进制,二进制是满二进一,所以他的每一位的权重其实是以 2 为权重的,就是下边的样子。
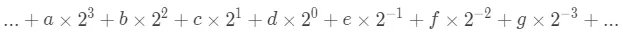
a,b,c … 代表0和 1中的一个,现在的数量是 a 个 8,b 个 4,c 个 2 ……
所以1100如果用十进制表示,就是 1 个 8 加上 1 个 4,也就是12了。这样的话,我们就可以理解他买了多少苹果了。
十进制转二进制
那么十进制怎么转换成二进制呢?最开始的问题,怎么用二进制去表示 2019.723。
整数的转换
其实这就是数学上的问题了,首先我们考虑整数部分2019。根据前边二进制转十进制的公式,我们知道可以有下边的等式。
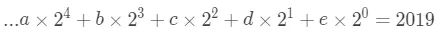
两边如果同时除以 2 会发生什么呢,
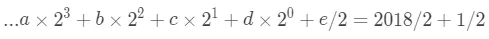
可以看到系数是 a,b,c,d的部分都整除了,只剩下 e/2。
右边的话,把2019分成两部分2018和1。然后就是 和
和 两部分。
两部分。
左边也看做 和
和 两部分。
两部分。
左右两部分对应相等。
右边的部分。
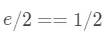
所以算出了  。
。
再看左边的部分。
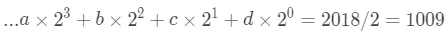
我们可以两边继续同时除以2,就可以求出d。同理就可以求出a,b,c以及更多的系数。
再来回想一下我们的方法,两边同时除以2,然后被分成 和
和 两部分,其实左边就是商,右边是余数。
两部分,其实左边就是商,右边是余数。2018/2=1009······1,对应等式左边的部分,e 其实就等于余数。
所以转换的方法就是用2019除以2,余数作为二进制的低位。商作为新的除数,继续除以2,余数作为二进制的低位…直到商为 0。

因为我们每次求出的都是二进制对应的低位,书写的话习惯于先写高位,所以倒着写过来 11111100011就是2019的二进制形式了。
写成代码的形式。
public static List<Integer> integerTrans(int n) {
ArrayList<Integer> list = new ArrayList<>();
while (n != 0) {
list.add(n % 2);
n /= 2;
}
for (int i = list.size() - 1; i >= 0; i--) {
System.out.print(list.get(i));
}
return list;
}
小数的转换
考虑完整数,再来想一下小数0.723怎么处理。同样的,利用二进制转十进制的公式,写出下边的等式。
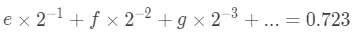
之前同时是利用两边同时除以2,对于上边的等式肯定不行了。换一下,两边同时乘以2呢?看看会发生什么。
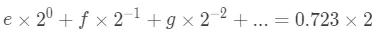
和之前一样,把两边分别分成两部分。
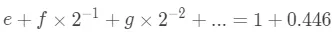
两部分分别对应相等,可以知道
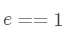
另外一部分的话
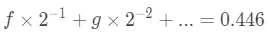
我们继续同时乘以2,变成下边的样子。
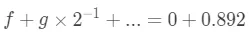
这样又可以求出 ,同样的一直不停的继续下去,直到得到的新的小数部分是
,同样的一直不停的继续下去,直到得到的新的小数部分是0。
所以我们的算法就是不停的乘2取整数部分,有可能得到的新的数永远不等于 0,这就取决于我们需要的精度了,可以随时停止。

小数的话正着写出来就可以了,0.1011就是十进制0.723的近似值了。
所以十进制小数转成二进制并不会像十进制整数那么顺利。原因的话,因为二进制小数它的权重依次是0.5,0.25,0.125…,所以只有这些数的任意相加才能被精确表示。大部分的十进制小数都不能精确的用二进制表示。
甚至看起来最简单的0.1如果转成二进制,会是什么样呢?

可以看到计算过程中,出现了循环,0.4,0.8,0.6,0.2会循环出现,所以0.1的二进制表示就是0.0 0011 0011 0011...是一个无限循环小数了。它就相当于我们十进制中的1/3,写成小数形式是0.3333333...。
用代码表示一下,我们只保留 10 位小数。
public static List<Integer> decimalTrans(double n) {
ArrayList<Integer> list = new ArrayList<>();
int count = 10;
while (count > 0) {
n = n * 2;
list.add((int) (n));
n = n - (int) (n);
count--;
}
for (int i = 0; i < list.size(); i++) {
System.out.print(list.get(i));
}
return list;
}
历史的发展
可以看一下现实生活中数字的发展,引自维基百科。
无位值十进制
古埃及十进制:以一个竖道代表1,二并排竖道代表2,三竖道代表3,一横道代表4,左二撇右竖道代表5,上三撇下三撇代表6,上下两道代表8,四个(并排代表9,一个“人”字形代表10,“人”上加一横代表20,20左加一点代表30,横道上加一点代表40,横道上加三竖道(如中国筹算的8)代表60,横道上加四竖道代表80(形同中国筹算中的9)代表80,两横道上加三竖代表90……。
古希腊十进制,1至9,10至90,100至900各有不同的单字母代表。
古印度Kharosshi十进制,以一个竖道代表1,二并排竖道代表2,三竖道代表3,一个X代表4,IX代表5,||X代表6,XX代表8,10,20个有单字符代表。
古印度和Brahmi十进制,和希腊十进制相似,1至9,10至90,100至900各有不同的单字母代表。符号很多。
非十进的进位制
巴比伦60进位制:以一个上大下小的楔形代表1,两个并列楔形代表2,三个并列楔形代表3,上二个楔形下二个楔形代表4,上三楔下二楔代表5,上三楔下三楔代表6,上四楔下三楔代表7,上四楔下四楔代表8,上五楔下四楔代表9;一个左小右大横楔代10,两个横楔并排代表20,三个横楔并排代表30,四个横楔并排代表40。
玛雅20进位制:以一个点代表1,两个点并列代表2,三点并列代表3,四点并列代表4,短横线代表5,横线上加一点代表6,横线上加二点代表7,横线上加三点代表8,横线上加四点代表9;上下两横线代表10,上下两横线之上加一点代表11,三重叠横线代表15,三横线上加一,二,三点代表16,17,18;小椭圆圈上加一点代表20。
十进位制
中国古代的十进制有书写式和算筹两种型式。
印度-阿拉伯十进位制。
结束
不得不感慨下人类的聪明,将量的概念抽象出来,不同地区的独立发展,最后又是那么的相像。所以数字,其实就是符号对数量的映射,并且人们达成了共识。
趣谈计算机负数表示:补码
小亮:小杨呀,考你个问题。
小杨:我不听,我不听,我不听。
小亮:非常有意思的,你听听。你说如果给你一个计算器,但只能算加法,那你减法该怎么办呀?
小杨:这么神奇的吗,你难道有方法?
小亮:其实原理很简单的,日常生活中我们其实一直都有用到的,你看一下现在闹钟几点了?

小杨:8 点!
小亮:那 3 小时前是几点呢?
小杨:8 - 3 = 5,5 点!
小亮:那 9 小时以后呢?
小杨:嗯嗯,你等等,一五得五,二五一十,五一劳动节,8 + 9 - 12 = 5,还是 5 点!
小亮:你为什么减去了一个 12 呀?
小杨:小学老师这样教我的呀,至于为什么?Emmmm,因为总共只有 12 个数呀!
小亮:就是这里,你完成了一个伟大的操作!模运算。你进行了模 12 操作,还有一个关键点,总共只有 12 个数!
小杨:我是不是很厉害,嘻嘻嘻,但是…然后呢?
小亮:你想一想,8 - 3 和 8 + 9 的结果是一样的,而最开始我给你的计算器只能进行加法操作,所以再进一步,把 8 - 3 当做 8 + (- 3),它和 8 + 9 的结果一致,所以…
小杨:所以我们用 9 去表示 -3,然后如果想计算减法 8 - 3,就直接在计算器上输 8 + 9,就可以得到正确结果了!
小亮:bingo!但你忘了一个前提,就是计算器必须只能存 12 个数,它会自动进行取模操作。还有一个事,现在是 8 点,4 小时后呢?
小杨:8 + 4 = 12,12 点!
小亮:咦?你为什么不进行取模了,你看之前还多减了一个 12 呢?为了统一操作,我们每次都进行取模吧,12 - 12 = 0,这样也比较符合取模的含义,这样对 12 取模,意味着我们数的范围就是 0 到 11 了。
小杨:好的,好的,我知道了,我现在只知道了 -3 可以用 9 表示,那我们想算 8 - 5 呢?-5 用多少表示呢?
小亮:你自己拨动下表针看看,5 小时前和几小时后是等价的呢?
小杨:我看看,7 点!算 8 - 5 的话,用 8 + 7 就可以了。好了,其他的我也知道了,来,我给你画张表。

小亮:哇,你是怎么把这个表列出来的?
小杨:因为是模 12 ,所以 1+ 11 = 0,1 - 1 = 0,所以 -1 用 11 代替,2 + 10 等于 0,2 - 2 = 0,-2 用 10 代替,其他也是这样的。
小亮:棒棒棒,那现在计算会有一个问题的,之前的 8 - 3,8 - 5,结果都是正的,没有问题。那如果,3 - 5 呢?
小杨:3 - 5,-5 对应 7,那就是 3 + 7 等于 10 ,看上边的表格,10 对应 -2,所以答案是 -2!骗子!明明没有问题!
小亮:那你 5 - 3 呢??? -3 对应 9,5 + 9 = 2,看下上边的表格,这时候你咋不进行 2 对应 -10 了。
小杨:因为我知道 5 - 3 是正的,3 - 5 是负的,嘻嘻嘻。
小亮:所以这就是问题所在了,既然要让计算器算,它肯定不知道是正的还是负的,所以这样肯定不行的。我们不能把每一个正数都对应一个负数,你看看下边这个表。

小杨:3 - 5 和之前一样,-5 对应 7,那就是 3 + 7 等于 10 ,10 对应 -2,然后的话,5 - 3 = 2,-3 对应 9,5 + 9 = 2,2 对应 2,哇!这次没有问题了。
小亮:是的,这次我们只是用一部分正数表示了负数,另一部分保持不变。每一个数都有了一个对应关系,9 不再是 9 了,它其实是 -3。但这有个缺点,给你一个数,你并不能立刻知道它代表几,只能去查表才会知道。
小杨:对呀,我用的计算机能算的数的范围非常大呀,它内部不会也有这样一个表格吧。
小亮:不不不,它实现了一种转换关系,给定一个数立马知道它代表的几。
小杨:那会不会很复杂呀,我想听听。
小亮:其实和那个钟表是一个意思的,计算机里寄存器存的位数是固定的,就像表盘的数是固定的。表盘里,11 点过 1 个小时后,就变成了 0 点,因为是进行的模 12 操作。如果寄存器只能存 4 位数字,那就总共可以表示 16 个数字,那么 15 再加 1 的话就变成了 0,那么怎么实现减法…
小杨:我懂了,一样的道理,用一部分数字来表示负数就可以了!
小亮:聪明!因为计算机里是都是用 2 进制存储的,我们来看看这些数字都长什么样子。
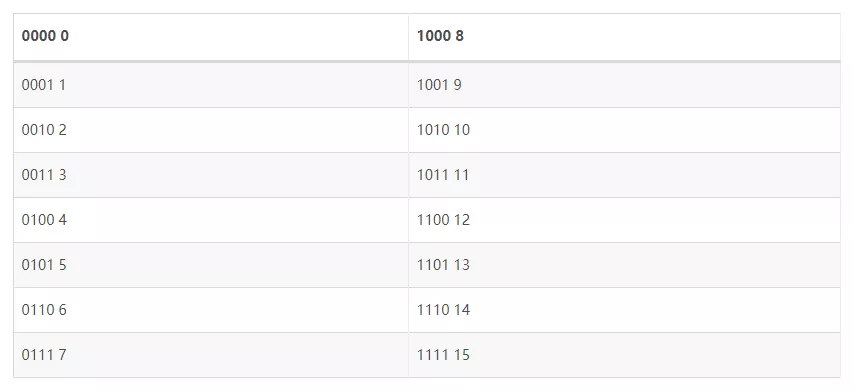
小杨:那我来分一下吧!
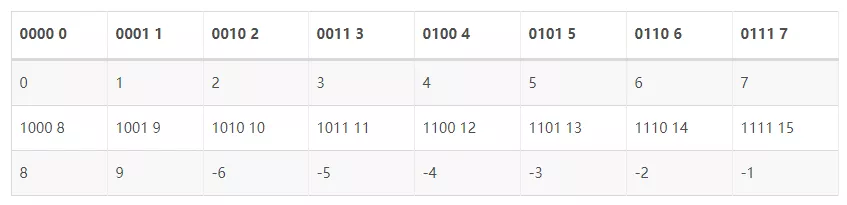
让我来算一个减法,7 - 4 = 7 + 12 模 16 = 3!哇,成功了!
小亮:等等,你为什么搞了 8 个正数,只搞了 6 个负数呀。
小杨:因为我喜欢!
小亮:那这样又回到之前的问题了,如果我问 8 代表的正数还是负数?你是不是还是只能查表呀。
小杨:对哦,那该怎么分呀。
小亮:很自然呀,你看上边表格的二进制部分,最高位是不是有的是 0 ,有的是 1,我们把最高位是 1 的正数来表示负数,最高位是 0 的数表示正数,是不是就可以了。
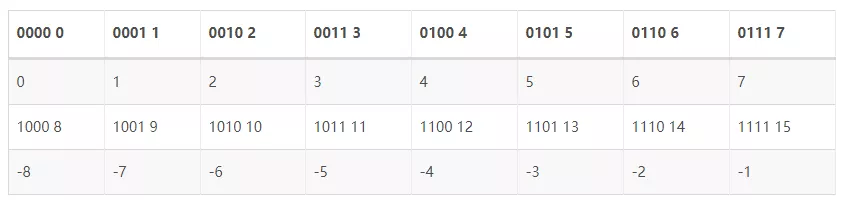
小杨:对呀,这样的话,给我一个数,我就知道它是负的还是正的了,比如 13,二进制是 1101,开头是 1,那它代表的一定是一个负数。那开始你说可以直接知道它代表的是几,该怎么算呢?
小亮:嗯嗯,你想一想,你得出表格的时候是怎么操作的呢?首先二进制开头是 0 的,它是几就代表几,就不讨论了。负数的话,你为什么用 12 表示 -4 呢?
小杨:因为现在是模 16 的,所以两数和如果是 16 的话,就会变成 0。12 + 4 = 16 = 0,-4 + 4 = 0,所以 12 可以代替 -4。
小亮:所以如果给你一个数,如果是二进制开头是 1,我们先确定它是一个负数,至于是负几,我们直接用 16 减它就够了!如果给你 13,我们看一下二进制是多少,1101,开头是 1 所以它是负数,负几呢?16 - 13 = 3,所以 13 代表 -3,看下上边的表格,是不是对的?
小杨:等等,这个我一直知道呀,之前表盘的时候我就是这样算的呀。16 - 13,我们是为了用加法表示减法,这怎么又出来减法了。
小亮:到了见证奇迹的时候了!让我们用二进制的形式看一下,16 - 13 = 1 0000 - 1101 = (1 + 1111) - 1101 = (1111 - 1101)+ 1 = 0010 + 1 = 0011 = 3。
小杨:哪里奇迹了,1111 - 1101,这不又出现减法了。
小亮:不不不,这步不用减法,只需要把 1101 按位取反就够了,也就是 0010!
小杨:神奇!所以我来总结下,给我们一个数,如果二进制开头是 0,那就不管了,它是几就是几。如果开头是 1,那它代表负数,负几呢?按位取反,再加一就够了!但还有个问题,现在给我一个数我只能它代表几,但反过来,给我一个数,我怎么知道用几去代表它呢?如果给我 -3,我们用多少代表它呢?
小亮:是同样的道理,13 + 3 = 16 = 0,-3 + 3 = 0,所以用 13 代表 -3。所以算的话,还是用 16 去减这个数,所以同样的推导,最后的结论是一样的,按位取反,末位加 1,-3 的话,根据推导我们是用 16 减去的 3,所以用 3 对应的 2 进制 0011,按位取反,1100,末位加一,1101,所以 -3 就用 1101 表示。
小杨:哇,懂了懂了,这样完美的把加法和减法统一了,只不过计算前进行数字的转换就够了。
小亮:对的,其实这就是补码,计算机中所有的整数都用补码存储,这样算减法用加法器就足够了。举个例子,3 的补码是 3 不变,也就是 0011,-4 的补码,4 的二进制按位取反末位加 1,也就是 0100 变成 1011,再加 1 变成 1100,所以算 3 - 4 = 3 + (-4)= 0011 + 1100 = 1111,1111 代表多少呢?首先肯定代表一个负数,然后按位取反末位加 1,就是 0001 了,所以结果就是 -1。
小杨:我明白了,只要学会把一个数转成补码,然后补码再还原就够了,而且两个转换的方法还一样,按位取反,末位加 1,很清晰了。
小亮:让我们回到真正的计算机里, 我们知道 int 一般情况是 4 个字节,也就是 32 位,一样的道理,我们把最高位是 0 的代表正数,最高位是 1 的代表负数,所以最大的正数就是 0111 1111 … 1111 1111,这个数代表多少呢?
小杨:这个我知道,为了方便计算,先把它加 1,变成 1000 0000 … 0000 0000,这个是 
小亮:那最大负数呢?
小杨:最大负数的话,因为 1 开头代表负数,然后其他部分当然越小越好,所以就是 1000 0000 … 0000 0000,那它代表多少呢?直接套用公式,按位取反,末位加一,变成 1000 0000 … 0000 0000,它竟然又变了回来,之前算了这个数是 
小亮:你想一下呀,0 开头的数和 1 开头的数,个数是不是一样的,但是 0 开头的数包括了 0,所以正数就少了一个咯。顺便再问你个问题,最小的负数是 -2147483648,那 -2147483648 - 1 是多少呢?
小杨:-2147483649!!哈哈,开个玩笑,我知道你是问我计算机里边的情况。我来算一下,-2147483648 的补码是 1000 0000 … 0000 0000,-1 的补码是把 1 按位取反末位加 1,就是 1111 1111 … 1111 1111,然后把这两个数加起来就是 0111 1111 … 1111 1111,这不是那个最大的正数吗,所以 -2147483648 - 1 是 2147483647!
小亮:感觉你出师了呀,竟然没中套。这其实也很好理解对不对
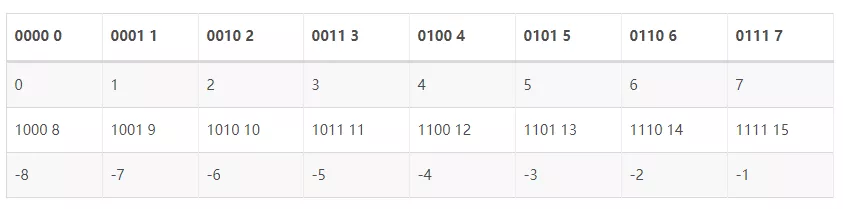
看上边的表格,这个只有 4 位,所以最大的数是 7,最小的数是 -8。上边的 7 后边是 -8 了,所以 -8 减 1,也就是 -8 前边那个数当然就是 7 了。
小杨:其实这个表格化成圆其实更好理解了,就像表盘一样,哈哈。
小亮:对的,总结一下,其实我们利用了寄存器存的位数是有限的,所以它到达最大的数以后会自动置零,相当于完成了取模操作,就像钟表一样,到了 11 点,之后又会从 0 点开始。然后我们再定义用哪些数表示正数,哪些数表示负数,从而完成了加法和减法的统一。并且做到了给一个数知道它的补码表示,知道补码,也可以算出它代表几。
小杨:那计算机设计补码的时候就是这样想的吗?
小亮:这我就不知道了,但可能和我想的一样?哈哈哈。最后留给你一个题,不用乘法除法也不用减法怎么求一个数的相反数呢? -2147483648 * (-1)等于多少呢?
追本溯源:字符串及编码
开始
先考虑下边的问题。
1
|
let s = "js"
|
我们知道 length 就是字符串的字符数,所以输出的依次是 2,1,1,对吗?
探索一
我们知道,计算机里只能存 0 和 1,换言之,只能存数字,而我们现在在屏幕上看到的文字只是将数字对应到图形而已。
早期的 ASCII 码就是典型的例子,如下图,为了书写方便我在数字前边加了 0x 代表是 16 进制。
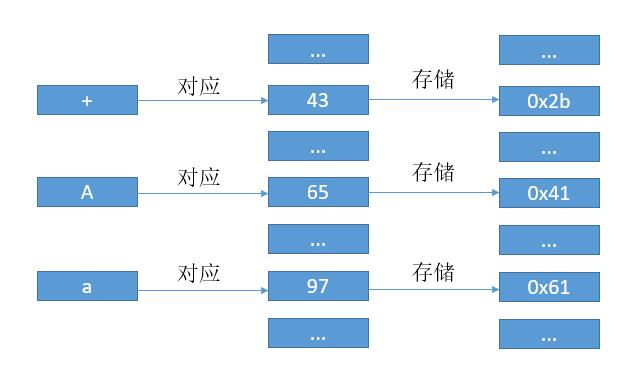
我们用 106 代表 ‘ j ‘,115 代表 ‘ s ‘。然后如果用 ASCII 码表示 “js” 的话,其实就是 0110101001110011 ,然后每 8 位也就是一个字节组成一个数字,根据对应关系电脑把本来的数字转换成了字符 “js” 展示到了我们面前。
有一个缺点就是 ASCII 码是 8 位,那么只能表示 2828 个数字,也就是 256 个数字,这对于英文字母已经足够了。但是对于汉字的话,还远远不够。
探索二
所以我们加 1 个字节,用两个字节的数字去对应汉字,216216 也就是 65536,肯定足够了。
当然,每个国家都会这样想,然后都制定了自己的语言相应的对应规则,这当然不方便大家在互联网上互通有无,如果本机不知道对应国家的编码对应关系,从而会造成乱码。所以后来有了 Unicode。
我们用 0x000000 - 0x10FFFF 这么多的数字去对应全世界所有的语言、公式、符号。然后把这些数字分成 17 部分,把常用的放到 0x0000 - 0xFFFF,也就是 2 个字节,叫做基本平面 (BMP)。从 0x010000 - 0x10FFFF 再划分为其他平面。

和 ASCII 码一样,我们可以把每个符号对应于一个数字,这个数字我们也把它叫做码点值。
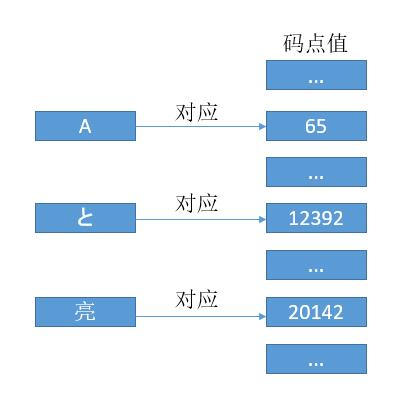
有了对应关系,我们可以像 ASCII 码那样去存了。当然这里的话因为每个字符都对应 24 比特位的数字,所以我们就用 3 个字节去存它吧。但是考虑到 CPU 的寄存器都是 8 位,16 位,32 位。。。翻倍来的,所以即使用 24 位,最终还得转到 32 位,所以我们直接用 32 位吧。
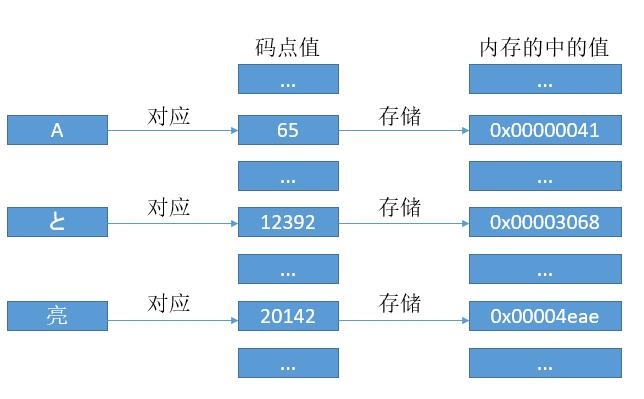
是的,这就是传说中的 UTF - 32 编码,简单明了,码点值是多少,内存中就存多少。
探索三
UTF - 32 缺点很明显了,字母 A 原本只需要 1 个字节去存储,而现在却用了 4 个字节去存,大部分位置都是 0。
我们为什么要多存那么多零呢?能不能 A 只存 0x41,亮只存 0x4eae。如果 A亮这个字符串放到内存中就是 0x414eae。问题来了,计算机怎么知道,几个字节代表一个字符呢?是 0x41呢?还是 0x414e 呢?还是 0x414eae?
于是,就有了 UTF - 8,将码点值进行一定的转换再去存储。
把阮一峰老师的讲解搬过来。
1
2
3
4
5
6
7
8> Unicode 符号范围 | UTF-8 编码方式
> (十六进制) | (二进制)
> ----------------------+---------------------------------------------
> 0000 0000 - 0000 007F | 0xxxxxxx
> 0000 0080 - 0000 07FF | 110xxxxx 10xxxxxx
> 0000 0800 - 0000 FFFF | 1110xxxx 10xxxxxx 10xxxxxx
> 0001 0000 - 0010 FFFF | 11110xxx 10xxxxxx 10xxxxxx 10xxxxxx
>
根据上表,解读 UTF-8 编码非常简单。如果一个字节的第一位是
0,则这个字节单独就是一个字符;如果第一位是1,则连续有多少个1,就表示当前字符占用多少个字节。下面,还是以汉字
严为例,演示如何实现 UTF-8 编码。
严的 Unicode 是4E25(100111000100101),根据上表,可以发现4E25处在第三行的范围内(0000 0800 - 0000 FFFF),因此严的 UTF-8 编码需要三个字节,即格式是1110xxxx 10xxxxxx 10xxxxxx。然后,从严的最右边二进制位开始,依次从右往左填入上边格式中的x,多出的位补0。这样就得到了,严的 UTF-8 编码是11100100 10111000 10100101,转换成十六进制就是E4 B8 A5。
让我们再看下「亮」,码点值是0x4eae,二进制就是 100111010101110,同样符合第三行,即格式是1110xxxx 10xxxxxx 10xxxxxx。从亮的最右边二进制位开始,依次从右往左填入上边格式中的x,多出的位补0。这样就得到了,亮的 UTF-8 编码是 1110(0100) 10(111010) 10(101110),16 进制就是 e4 ba ae。
所以现在的对应关系变成了下边的样子。
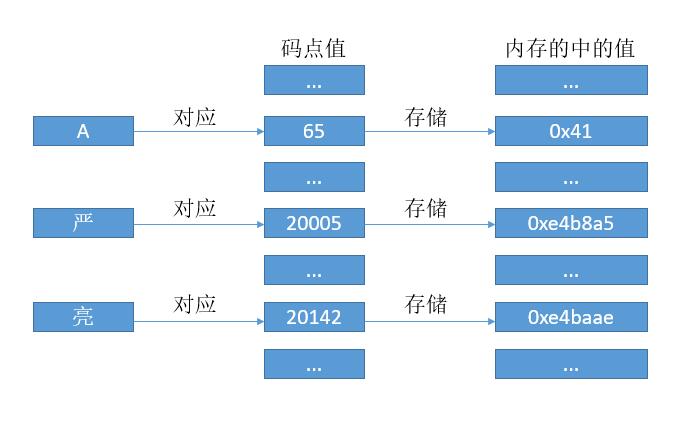
和 UTF - 32 不同之处在于,我们不再用 4 个字节存储码点值,而是通过规则转换后再存储,这样的好处就是之前的A的话就只需 1 个字节就够了,而其他的可能是 2 个或 3 个,4 个字节,所以 UTF - 8 也叫变字长编码。
由于 UTF - 8 的变字长,而对于大部分常用字符都是 1 或 2 个字节,所以对于 html、邮件的传输多用 UTF-8 进行编码后传输。
探索四
UTF - 8 有什么缺点吗?
对于一个字符串abc天气不错,如果我们知道它的总共大小是 19 字节,但是我们很难算出它有多少个字符。因为有的字符是 1 个字节,有的是 2 个字节,有的是 3 个。所以为了知道字符数,我们还需要遍历一遍所有字节,从而确定有多少个字符。此外如果我们想取第 3 个字符,我们还是得从第 0 个字节开始遍历,因为我们不知道每个字符有多少字节。
如果每个字符都用固定长度编码就好了,这不又回到 UTF - 32 了吗?不不不,我们折中一下。
对于 Unicode 字符集,基本平面是我们常用的一些字符,用两个字节就可以编码。所以对于亮字的话,码点值是0x4eae,那么我们内部就用 0x4eae 去存。而 ASCII 码只需要一个字节,那么我们把通过高位补零扩充至两个字节去存。例如A的码点值是 65,16 进制对应 0x41,用 U+41 表示。那么内部的话就用 0x0041 去存。
那么基本面以外的字符呢?比如𫠂这个字就属于基本面以外,它的 Unicode 码点值是 178178,也就是 0x2b802 ,显然用两个字节是存不下的,那怎么办呢?
用四个字节存呗,像 UTF - 32 那样直接存码点值,然后高位补零吗?显然不行了,因为第一平面我们是用的两个字节,如果第一平面外的直接用四个字节去存码点值的话,可能会导致前两个字节和基本面的两个字节重复,导致我们无法区分当前字符是两个字节还是四个字节。
UTF - 8 中,我们根据二进制开头的 1 的个数来表示当前字符是几个字节。这里的话,幸运的是在第一平面 U+D800..U+DFFF 的值不对应于任何字符。所以我们可以根据一些算法,把码点值转换为 4 个字节,前两个字节就用 U+D800..U+DFFF 中的值,这样如果前两个字节是 U+D800..U+DFFF 范围内的数,那就意味着该字符是 4 个字节编码的。否则就是两个字节。
这就是 UTF - 16 的编码方式了(具体的算法大家可以网上找一下),相对于 UTF - 8 的优势就是固定字节数,大部分字符都是两个字节。所以如果对于一个字符串abc天气不错如果采用 UTF - 16 编码,我们知道了它的总大小是 14 字节,那么字符数就很好知道了,它的大小除以 2 就是它的字符数了。而取第 4 个字符,如果知道了字符串开头的地址,也只需要加 2 * 4 就可以了(下标从 0 开始)。对于字符串的切割合并也都很好操作了。
所以对于一些语言 java,javascript 里的字符串也都用了 UTF - 16 编码。所以回到最开始的问题。
1
|
let s = "js"
|
那么就取决于这些字符是不是在第一平面内了,如果是的话,那么结果就会就是 2 1 1。遗憾的时 “𫠂” 并不在基本平面,所以它内部是用四个字节编码,而 js 为了方便简单,它简单粗暴的认为两个字节就是一个字符,所以输出的就是 2 了。
此外关于,Unicdoe 所有的字符的码点值可以在 这个 网站找到。
实验验证
接下来说一下文件的存储。
我们打开一个 .txt,看到很多文字、符号,而内部其实也是用 0、1 存储的。既然要存储,就需要把 Unicode 的码点值进行编码。
如果是 UTF - 8 编码,那么一个码点值会生成 1 个或多个字节,然后把这些字节按顺序存就可以了。
如果是 UTF - 16 编码呢?
我们知道一个 Unicode 的码点值会对应一个数字,对于基本平面的字符,我们直接把这个数字存到内存中。那么问题来了,我们知道亮的码点值是 20142,换成 16 进制就是 0x4eae,内存中是按字节进行编址的。所以我们是先存4e呢?还是ae?先存4e吧,这样就符合我们人类阅读顺序,先读4e,所以先存4e呗。所以在内存中就是下边的样子。
1
|
内存地址 内存值
|
那么问题又来了,计算机处理的话先读取的是低地址,也就是4e,而4e对应数字0x4eae的高位(如果是 10 进制,个十百千,千就叫做高位)。有时候我们希望从低位读(也就是十进制中的个位)数字,所以我们希望这样去存。
1
|
内存地址 内存值
|
这就是多个字节存储的时候的字节序问题,把数字的高位存到低地址,低位存到高地址,叫做大端序(big endian),存储顺序符合我们人类习惯。反之就叫小端序(little endian)。
如果把亮字存到一个 .txt 中。
如果用 UTF-8 编码,那么前边算过的,就是e4 ba ae。
如果用 UTF-16 编码,大端序的话就是4eae。
如果用 UTF-16 编码,小端序的话就是ae4e。
我们可以验证一下,可以用 notepad++,安装一个 HEXEditor 插件即可。或者其他的可以查看内部编码的也行。
写一个亮到 text.txt

以 UTF - 8 编码。
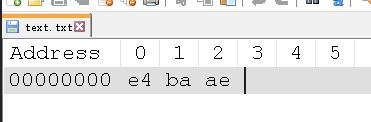
如果用 UTF - 16 编码,大端序
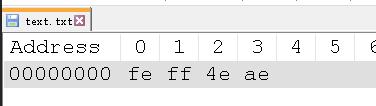
如果用 UTF - 16 编码,小端序
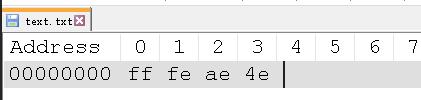
可以看到 UTF - 16 编码的时候,除了本身的字节,最开头还多了两个字节,ff和fe。原因很直接了,就是为了区分大端序和小端序。feff代表大端序,fffe代表小端序。
feff和fffe也叫做 BOM,它可以区分不同编码。我们也听过 UTF - 8 无 BOM 或者 UTF - 8 BOM。UTF - 8 的 BOM 是 EF BB BF,windows 记事本编写的 .txt ,如果以 UTF - 8 编码保存,它默认就是有 BOM 的,所以如果看他的内存存储就是下边的样子。

而 UTF - 8 并不存在字节序的问题,因为它的最小编码单位就是字节,而 UTF - 16 编码最小单位是两个字节,所以有字节序的问题,从而加了 BOM 来区分是大端序还是小端序。但是 UTF - 8 并不需要区分大端序还是小端序,所以可以不需要 BOM。如果加了 BOM,对于一些读取操作,它可能会把读取到的 BOM 认为是字符,从而造成一些错误。所以我们保存 UTF - 8 编码的文件时,最好选择无 BOM。
我们也可以在浏览器的控制台上直接验证,因为 js 允许我们直接给字符串赋 Unicode 的码点值。格式是 \u 加上 16 进制的码点值即可。对于超过 2 个字节的码点值,用大括号括起来。
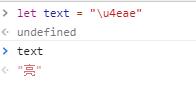
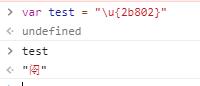
我们所熟知的 emoji 表情其实在 Unicode 字符集上也有对应的码点值。
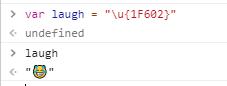
比如最常用的笑哭脸的码点值是 U+1F602,当然 Unicode 只规定了码点值,并没有规定怎么实现,不同平台对于笑哭的表情展现也是不一样的。

同样我们也可以在浏览器上进行验证。
更多好玩
知道了上边的编码原则,我们就可以做些有趣的事情了,还记得「神奇字体」小程序吗?可以生成不同样式的字体,在微信、知乎发送。

𝙄 𝙡𝙤𝙫𝙚 𝙮𝙤𝙪 𝙩𝙝𝙧𝙚𝙚 𝙩𝙝𝙤𝙪𝙨𝙖𝙣𝙙
其实上边的每一个字母并不是对应 ASCII 码值,而是对应基本平面外的 Unicode 码点值。所以我们如果输出上边的 I 字母,”𝙄”.length,输出的就是 2,因为它是基本平面外的字符,用了 4 个字节编码。
大家可以回顾下,我之前写的探索过程,就会明白「神奇字体」的原理了。
此外,Unicode 还有一些组合字符、控制字符,实现不同字符的组合,比如删除线、下划线和字符的组合,实现字符的逆序输出等等,大家可以自己去探索下,蛮有意思的。
结束
以上就是字符串编码的全部了,这里只介绍了 ASCII,Unicode,UTF 系列,其他的编码方式还有 GBK,GB2312,Big5,ISO 8859-6 等等,这块内容真的是太多太多了,大家感兴趣的话可以自己再去找找资料,上边我总结的如果发现问题可以及时和我反馈,感谢。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号