#QBXT2020寒假 Day2

Day 2 Afternoon

最大公约数，最小公倍数

描述

如果d是能同时整除a, b中最大的正整数，我们称d为a和b的最大公约数，记作d = gcd(a, b)

实现方式

辗转相除法

证明：若有\(a\mid b\)且\(c\mid b\),则\(a\pm b \mid c\)。

int gcd(int a,int b){
		return b == 0? a:gcd(b,a % b);
}

复杂度：(看这里)

推论：gcd(a,b) \(\times\) lcm(a,b) = a $\times $ b

证明：

\[lcm(a,b) = \frac{a}{gcd(a,b)} \times b \]

唯一分解定理

任意一个正整数x，都可以唯一地分解成\(p_1^{a_1} \times p_2^{a_2} \times … \times p_n^{a_n}\)的形式，其中\(p_1\)到\(p_n\)是素数（不考虑素数之间的顺序）

还有

\[a_1 + a_2 + … + a_n = O(\log x) \]

NOIP2001 最大公约数和最小公倍数问题

输入两个正整数x, y，问有多少对正整数以x为最大公约数，以y为最小公倍数
x <= 10^5, y <= 10^6

求出x * y,枚举y的因子作为一个答案，另一个易知，然后判断是否符合题意。

NOIP2014 比例简化

在社交媒体上，经常会看到针对某一个观点同意与否的民意调查以及结果。例如，对某 一观点表示支持的有 1498 人，反对的有 902 人，那么赞同与反对的比例可以简单的记为1498:902。
不过，如果把调查结果就以这种方式呈现出来，大多数人肯定不会满意。因为这个比例的数值太大，难以一眼看出它们的关系。对于上面这个例子，如果把比例记为 5:3，虽然与 真实结果有一定的误差，但依然能够较为准确地反映调查结果，同时也显得比较直观。
现给出支持人数 A，反对人数 B，以及一个上限 L，请你将 A 比 B 化简为 A’比 B’，要求在 A’和 B’均不大于 L 且 A’和 B’互质（两个整数的最大公约数是 1）的前提下，A’/B’ ≥ A/B 且 A’/B’ - A/B 的值尽可能小。
1 ≤ A ≤ 1,000,000，1 ≤ B ≤ 1,000,000，1 ≤ L ≤ 100，A/B ≤ L

写一个结构体模拟分数，重载运算符进行运算、比较大的操作，暴力枚举1-100的数字即可。

ll gcd(ll a,ll b){
		return b == 0 ? a : gcd(b,a % b);
}
struct frac{
		ll a,b;
};
frac operator +(frac x,frac y){
		ll n = x.a * y.b + x.b * y.a;
  	ll m = x.b * y.b;
  	ll z = gcd(m,n);
  	n /= z,m /= z;
  	return (frac){n,m};
}//lcez_cyc
bool operator <(frac x,frac y){
		return x.a * y.b < x.b * y.a;
}

高精度

另外附数据类型

int 范围是-2^31-1~2^31-1
long long 范围是-2^63-1~2^63-1
unsigned int 范围是0~2^32-1
unsigned long long 范围是0~2^64-1

来来来看我博客。我应该今天没时间再写一遍了。

别忘了处理进位借位问题

高精除以单精没写过。

还有这么一波骚操作

Bignum operator/ (Bignum x,int y){// 带重载运算符的高精除以单精
Bignum z;
z.1en=x.1en; τ
for(int i=z.Ien;i;i一)
Z.a[i]=x.a[i]/y;
x.a[i一1]+=x.a[i]%y;
while(z.1en>1&&z.a[z.1en]==0)z.1en一;return z;|
}

//高精除以高精//复杂度也是线性的。
bool operator <= (Big x,Big y){
		if(x.len < y.len) return 0;
  	if(x.len > y.len) return 1;
  	for(int i = 1;i <= n; i++){
				if(x.a[i] != y.a[i])
          return x.a[i] <= y.a[i];
    }
  	return 1;
}
Bignum operator/(Bignum x,Bignum y)
{
	Bignum z;
	z.len=x.len;
	for(int i=z.len;i;i--)
	{
		for(int k=9;k>0;k--)
		if(shift(y,i-1)*k<=x)
		{
			z.a[i]=k;
			x=x-shift(y,i-1)*k;
			break;
		}
	}
	while(z.len>1&&z.a[z.len]==0)z.len--;
	return z;
}

读入读出都是倒序。

压位

一个int只存储0到9的数字位，使得我们的程序空间和时间效率都不高

int的最大范围可以达到2147483647，所以一个int存储8位是没问题的

在读入和输出的时候要注意，除了最高位之外要补0

很显然我不想尝试

高精度最大公约数

Stein算法：
求最大公约数的算法，好处是只需要用到减法和高精除以单精；算法描述为：

若a和b都是偶数，则记录下公约数2，然后都除2

若其中一个数是偶数，则偶数除2，因为此时2不可能是这两个数的公约数了

若两个都是奇数，则$a = \mid a-b\mid \(，b = min(a,b)，因为若d是a和b的公约数，那么d也是\)\mid a-b\mid $和min(a,b)的公约数。

进制转换

就那样。粘PPT

P进制下的a1a2…an代表的数字是\(a1 * p^{(n-1)} + a2 * p^{(n-2)} + … + an\)

高精的进制转换

假设从p进制转换到q进制

如果一个long long能存下：先转换到10进制再转换到q进制

如果一个long long不能存下：模拟除法除q的过程

凑硬币

有面值为1, 5, 10, 50, 100, 500, 1000, 2000的硬币，已知每种硬币有多少个
要用最多的硬币凑出面值p，无解输出−1

最少的话，贪心就好了。

最多的话，先计算所有硬币全部拿来的总和，从大到小（按照面值从大到小）依次贪心地减到要求的值（因为所有的硬币面值都两两成倍数关系，所以大的一定可以被小的替代）

凑硬币加强

有面值为1, 5, 10, 20, 50, 100, 200, 500, 1000, 2000的硬币，已知每种硬币有多少个，要用最多的硬币凑出面值p，无解输出−1

问题在于用的50和500用的个数的奇偶性（因为他们不能够两两成倍数关系）

首先枚举50和500的奇偶性，然后从大到小选择。

补集转化，求最少用多少硬币凑出S − p

① 如果没有面值500和50这就是一个普通贪心

② 强制50和500选奇数个还是偶数个，把符合要求的50或500的个数加起来，转化成贪心

题

有n种面值Vi 和颜色Ci 的硬币，每种硬币有无穷多个

接下来有Q种询问，选出一组面值为S的硬币，最小化选出硬币的颜色种类数\(，，1≤n≤30，1≤Vi ≤2×10^5，1≤S ≤10^{18}\) 这个题？？？？回头说？？

怎么判断是否能选出一组面值为S 的硬币
S很大，需要从硬币面值入手，选出一个面值最小的硬币，设为m，接下来就可以在模m意义下进行DP
fij表示用了i种颜色，拼出面值模m为j的最小面值

同余

思想

如果a和b模m之后的数值是相等的，那么a和b模m同余

OI里很多题目需要取模，需要用同余的结论（ \equiv 是\(\equiv\)）

同余的等价

同余是模意义下的等价关系

很多运算在同余意义下也存在等价的运算

除法（等价于乘以逆元）

开根号（等价于求模方程的根）

对数（等价于离散对数）

逆元

在模意义下，一个相当于\(\frac 1a\)的数

记a的逆元为\(a^{-1}\)

逆元满足\(a * a^{-1} = a^{-1} * a = 1 (mod \ p)\)

逆元怎么算？

此处飞马小定理(大雾)

\[a^p \equiv p \pmod p\\a^{p-1} \equiv 1 \pmod p \\ (要求p是质数且a、p互质) \]

则a的逆元就是 \(a^{p-2}\)

所以可以使用快速幂

扩展欧几里得算法

即：解方程：

\[ax + by = gcd(a,b) \]

考虑当b = 0的时候，x = 1，y = 0（y的值是随便赋的）

假设\(bx' + (a \% b)y' = gcd(a,b)\)有解，则

\[a\ \% \ b=a-\lfloor \frac {a}{b}\rfloor\\bx′+(a-\lfloor \frac {a}{b}\rfloor)y′ = gcd(a,b)\\整理得\\ay'+b(x'-\lfloor \frac{a}{b} \rfloor*y')=gcd(a,b) \]

即可得对应的推导公式

代码：

扩展欧几里得求逆元

有

\[a \times a^{a-1} = 1 \pmod p \\a \times a ^{a-1} + p \times y = 1 \]

即求当a,b互质的时候，扩展欧几里得算法的求解。

需要逆元的场合

组合数取模

组合数

定义

C(n,m) 表示n个相同的小球中取出m个的方案

\[C_n^k = \frac{n!}{k! \times (n-k)!} \]

证明：首先考虑k个位置，第一个有n种可能，第二个有（n-1）种可能，类推得

\[X = n \times (n-1) \times (n-2) ······ \times (n-k+1) \]

然后又有这种取法得到的排列是去重之后的k!倍，所以最终组合数为上

组合数取模运算

因为

\[C_n^k = \frac{n!}{k! \times (n-k)!} \]

所以因为取模，所以应该找这些阶乘的逆元。为了优化，我们得到了：

\[(n!)^{-1} \times n = (n-1)! \\n!^{-1} = (n+1) ! \times (n + 1) \]

这样就得到了n的阶乘的逆元(或者说与任意逆元模意义上的相同值)

如果n、k更大了，就引入卢卡斯定理（正确性证明不需掌握）

\[C_m^n = C^{n \% p}_{m \% p} \times C^{\lfloor \frac mp \rfloor}_{\lfloor \frac np \rfloor} \]

因为观察公式可得，这种求法就是把m，n转换成p进制求解，所以复杂度为\(O(\log p)\)

路径数问题

给定\(n \times m\)的矩阵，求从左上角走到右下角的方案数。

答案为\(C_{max(m,n)}^{min(m,n)}\).我懒，不证明。

变式：

若给定坐标系一点D(x,y),给定直线y = x + k ，求不经过这条线的所有方案数

作D点关于与直线的对称D'，D的方案数减去D'的方案数就是答案。

插板问题：

详见初赛篇一本通我也不知道多少页

筛法

暴力筛

枚举\(\sqrt{n}\)以内的数，复杂度为\(O(n \log n)\)

线性筛(有时间自己复习一下今天真的来不及了)

memset(check,false,sizeof check);
int tot = 0;
for(int i = 2;i<=N;++i) {
    if(!check[i]) prime[tot++] = i;
    for(int j = 0;j<tot;++j) {
        if( i * prime[j] > N ) break;
        check[ i * prime[j] ] = true;
        if( i % prime[j] == 0 ) break; 
    } 
}

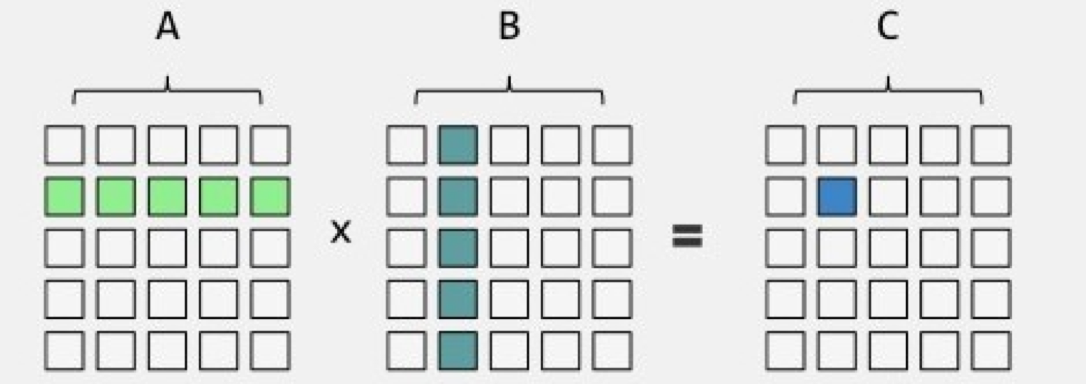
矩阵乘法

记住这个就行了。