6.19 考后总结

时间安排

7:10--7:30
读题，T1，T3不知道是啥。T2是博弈结论题。
7:30--8:00
T1,枚举距离后是个最大独立集问题，这玩意不可做。如果是二分图可以网络流，然而这不是二分图。
8:00--10:30
T2,显然答案只和出现的数的种数有关，先把送的 55 暴力分拿了。
然后开始猜结论，显然如果全 1 或全 2 先手必败，然后发现小范围内只有 {4,8} 特殊，必败，猜测只有这几种情况，暴力打表发现非也。
猜测先手必胜等价条件为存在某个模数使得所有 ai 在模意义下为 {0,1} 或 {0,2} 。暴力打表发现 n<=4 时结论成立，更大的规模打不出来了。
于是考虑 dp ，枚举模数，于是发现存在重复，考虑对模数的因子做容斥，发现这样容斥不太对。
然后就寄了。
10:30--11:00
T3,有状压暴力。考虑二分答案，然后考虑能不能直接贪心，不过仍与区间的位置有关，应该选取的区间的集合是不可知的。做不了。
11:00--11:40
T1,莫名想到枚举距离后，对一定范围内数点，然后发现这个“范围”是个圆，不会做。

回顾反思

T1:
考虑这样的最大团在二维平面上一定存在一对距离最大的点。
那么枚举这样的点对 (a,b) ，只考虑距离 a,b 均不超过这样的距离的点。
然后神奇的地方在于，对这些点求最大独立集的图是二分图。
证明考虑几何 :

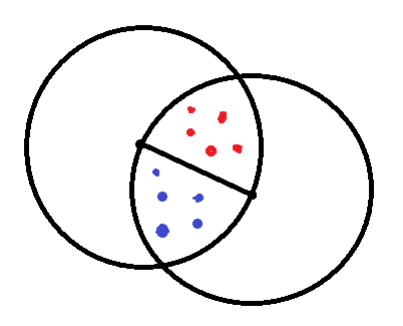
圆心分别为 (a,b) ，被圆心连线分割的两部分内部任意两点距离小于距离 lim 。

另外，每次随机一个加点的顺序，不停加点直到不再是团，这样一个随机化求最大团算法貌似能拿很高的分数。

T2:
[ARC134E] Modulo Nim
考场上一直在推必胜的等价条件，然而正解并没有给出等价条件，在得到几个必败的必要条件后，将答案规模缩到较小的范围内，然后暴搜状态 dp 求解。
容易有几个必要条件:
为 4 的倍数；对 3 取模同时存在 {1,2} 或者都变为 0；
整理得到 1. 为 {4,8} 2. 为 12 的倍数。
然后值域很小， 12 的倍数很少，直接暴搜状态 dp 。

T3:
没性质就不可做。

首先可以观察出来，若两个区间都翻转，那么其必然有交，否则答案更劣。
于是可以枚举一个交点 t ，和翻转的个数 cnt ，这样要考虑的区间集合已知即包含 t 的区间，贪心求解。
这样暴力复杂度比较高。
然后经过进一步最优性分析发现 t 和 cnt 的可选集合是 \(O(1)\) 级别的。
然后就能省掉两维复杂度，就能过了。
详细参考 LPF 的博客 「JOISC 2017 Day 2」门票安排

听说退火能拿一半分。