6.14 考后总结

时间安排

7:10--7:40
T1,感觉是诈骗题。
T2， dp 。
T3，不知道是啥。
7:40--8:20
猜想答案唯一，暴力验证正确。容易用栈维护，有点卡常。
8:20--10:40
T2，显然缩环之后就是点的 dag 计数。
感觉是个典的问题但我不会。关键在于点的 dag 计数怎么做。
想到可以将 dag 按照拓扑的等级分层，每次枚举一层的状态。
然后得到一个非常垃圾的 \(n^6\) 做法。
没比暴力强多少。
10:40--10:50
T3,先把暴力写了。
10:50--11:30
考虑怎么优化，突然发现可以预处理优化到 \(n^5\) 。
依旧非常之垃圾，和暴力同分。
注意到下发了快速模，用上模板后从 2s 骤降到 0.5 s。
可以通过 n<=50 ,30 分。
考虑怎么优化，发现枚举的变量之间关系太强了，目测没有任何优化前途了。
所以说根本还是计数 dag 的方法太垃圾了。
11:30--11:40
T3,发现答案只和前缀最小值有关，对于随机的部分分可以暴力二分前缀最小值。感觉可以上个笛卡尔树什么的，但是不知道怎么动态维护前后缀最小值。
11:40--11:50
修 T2 的小锅。

回顾反思

T2:
赛时瓶颈在于不知道如何优美地计数 dag 。
先考虑普通的有标号 dag 计数(不要求连通)：
赛时是枚举每一层的状态，很没必要。
考虑任何 dag 必然有入度为 0 的点，去掉这层点后剩下的是个子问题。
钦定若干点入度为 0 ，比如钦定 i 个，那么这 i 个点和剩下的 n-i 个点随便连边，然后递归到 n-i 规模的子问题。但是这样实际上不能保证入度为 0 的恰好是这 i 个点，所以要用容斥的思想处理。

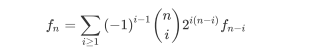
然后是每个 "点" 是环的版本：
那么实际就是若干个圆排列，把第一类斯特林数的贡献算上就行了。
题目限制 n 个点， m 条边，可以定义生成函数：

注意运用第一类斯特林数的性质。

有关的东西

T3:
注意到序列是个环，很难办。
但是最小值一定最后取，那么把最小值放在序列端点处，那么取的操作就不会跨越端点，变成一般的序列问题了。
算是个小技巧。

赛时瓶颈在于不知道怎么处理前后缀最小值。
发现一个区间最小值相当于一个隔板的作用。
那么按最小值分治，右边的贡献对左边是个常数，左边同理。
对于最小值，所属区间内前后缀最小值的位置是均摊 O(n) 的，可以暴力找出来计算答案就行了。

以最小值分治的笛卡尔树上，一个根在其子树对应区间一侧前缀最小值可以线性找出来。
以左侧前缀最小值为例，令根为 x ，则目标位置为：
ls(x),rs(ls(x)),rs(rs(ls(x))),rs(rs(rs(ls(x))))....
画图可发现显然。