十一周:振动合成与声速测量
实验名称:振动合成与声速测量
一、实验目的
- 了解简谐振动的叠加与形成的合成振动。
- 掌握同频振动与不同频率振动的合成规律,理解李萨如图形的本质。
- 理解驻波的形成条件与特点。
- 通过驻波法与行波法测量空气中的声速,并比较两种方法的差异。
二、实验仪器
声速测定仪、数字示波器、信号发生器、压电陶瓷换能器、连接线等。
三、实验原理
1. 振动的合成
(1)两个同频简谐振动合成
若质点同时参与两个同频振动:
\[x_1 = A_1 \cos(\omega t + \varphi_1)
\]
\[x_2 = A_2 \cos(\omega t + \varphi_2)
\]
合成振动为:
\[x = A\cos(\omega t + \varphi)
\]
其中振幅与初相位为:
\[A = \sqrt{A_1^2 + A_2^2 + 2A_1A_2 \cos(\varphi_2 - \varphi_1)}
\]
\[\varphi = \arctan\left( \frac{A_1\sin\varphi_1 + A_2\sin\varphi_2}{A_1\cos\varphi_1 + A_2\cos\varphi_2} \right)
\]
(2)两个互相垂直的同频振动
若:
\[x = A_3\cos(\omega t + \varphi_3)
\]
\[y = A_4\cos(\omega t + \varphi_4)
\]
可得轨迹方程:
\[\frac{x^2}{A_3^2} + \frac{y^2}{A_4^2} - \frac{2xy}{A_3A_4} \cos(\varphi_4 - \varphi_3) = \sin^2(\varphi_4 - \varphi_3)
\]
这是李萨如图形的基本方程。
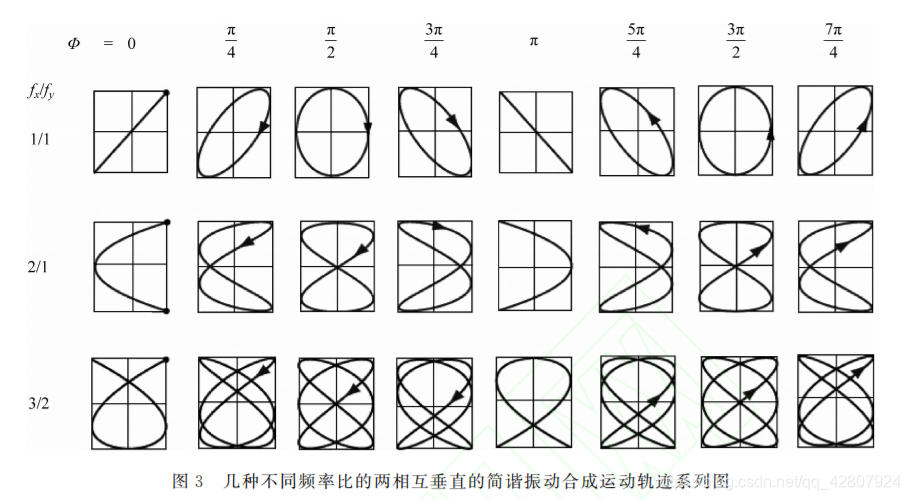
若频率比为整数:
\[\frac{\omega_y}{\omega_x} = \frac{N_y}{N_x}
\]
即可通过李萨如图形判断频率比。
2. 驻波的形成
两个反向行波叠加:
\[u_1 = A\cos(\omega t - kx)
\]
\[u_2 = A\cos(\omega t + kx)
\]
合成:
\[u = 2A\cos kx \cos\omega t
\]
空间因子为节振动(决定波节/波腹),时间因子为简谐振动。
波节位置满足:
\[kx = (2k+1)\frac{\pi}{2} \quad (k = 0,1,2,\ldots)
\]
相邻波节间距为:
\[\frac{\lambda}{2}
\]
可用于测定声波波长。
3. 行波法测声速
已知声波振动:
\[y_1 = y_0\cos(2\pi ft + \varphi)
\]
接收端相位差与距离关系:
\[\Delta \varphi = \frac{2\pi fx}{v} = \frac{2\pi x}{\lambda}
\]
当相位差变化一周(从 0 到 (2\pi))对应移动距离:
\[\Delta x = \lambda
\]
若相位差变化为 (\pi),对应:
\[\Delta x = \frac{\lambda}{2}
\]
4. 声速公式
直接法(温度修正):
\[v_t = 331.45\sqrt{\frac{t}{273.15} + 1} \quad (\text{m/s})
\]
理论声速:
\[v = \sqrt{\frac{\gamma RT}{M}}
\]
四、实验内容
-
驻波法:
- 调节声波,使压电换能器产生驻波;
- 通过观察驻波波腹变化位置,记录若干个波节间的距离;
- 由波节间距求出波长;
- 最终计算声速。
-
行波法:
- 利用示波器观察发射与接收信号的李萨如图形;
- 平移接收换能器,使图形变为直线或闭合曲线;
- 记录对应位置;
- 由相位差变化求波长,再求声速。
五、原始数据

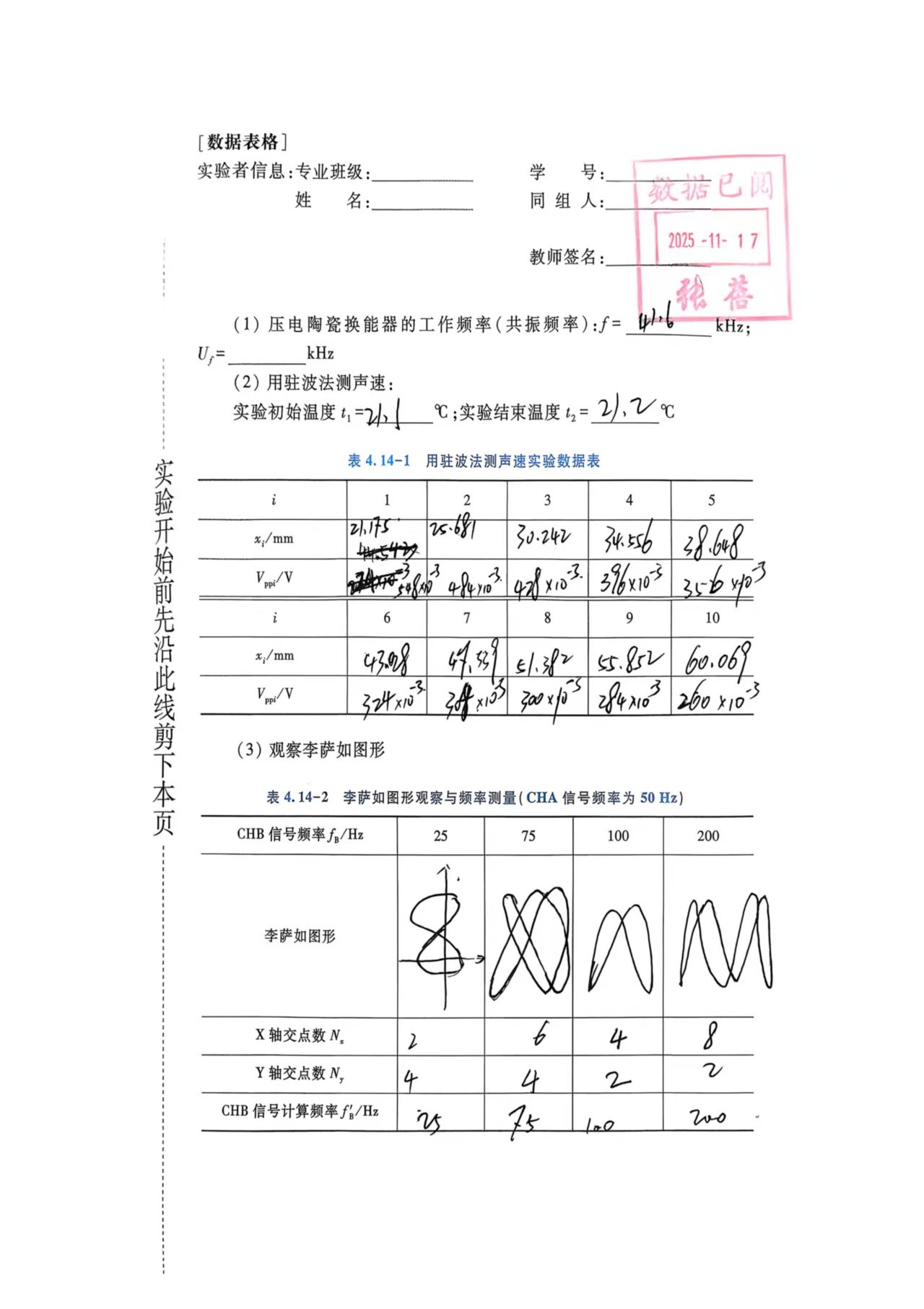
六、数据处理
1. 驻波法数据处理
驻波法利用压电陶瓷换能器在共振频率下形成驻波。相邻波节之间的距离满足:
\[\lambda = 2\Delta x
\]
实验记录的 10 个峰值位置与输出幅值如下:
| i | $x_i$/mm | $V_{\rm pp,i}$/V |
|---|---|---|
| 1 | 21.175 | 0.548 |
| 2 | 25.681 | 0.484 |
| 3 | 30.242 | 0.428 |
| 4 | 34.556 | 0.396 |
| 5 | 38.648 | 0.356 |
| 6 | 43.028 | 0.324 |
| 7 | 47.339 | 0.308 |
| 8 | 51.382 | 0.300 |
| 9 | 55.852 | 0.284 |
| 10 | 60.069 | 0.260 |
相邻峰值差计算:
\[\Delta x_i = x_{i+1} - x_i
\]
得到:
| 区间 | $\Delta x_i$/mm |
|---|---|
| 1–2 | 4.506 |
| 2–3 | 4.561 |
| 3–4 | 4.314 |
| 4–5 | 4.092 |
| 5–6 | 4.380 |
| 6–7 | 4.311 |
| 7–8 | 4.043 |
| 8–9 | 4.470 |
| 9–10 | 4.217 |
求平均:
\[\overline{\Delta x}
=\frac{1}{9}\sum_{i=1}^9 \Delta x_i
=4.322\,{\rm mm}
=4.322\times10^{-3}\,{\rm m}
\]
故实验波长为:
\[\lambda = 2\overline{\Delta x}
=8.644\times 10^{-3}\,{\rm m}
\]
压电陶瓷换能器的共振频率(实验记录):
\[f = 41.16\,{\rm kHz}
=4.116\times 10^{4}\,{\rm Hz}
\]
因此驻波法测得声速:
\[v = f\lambda
=4.116\times 10^{4}\times 8.644\times 10^{-3}
=355.6\;{\rm m/s}
\]
实验时温度:
\[t_1=21.1^\circ{\rm C},\quad t_2=21.2^\circ{\rm C}
\]
取平均温度:
\[t'=\frac{t_1+t_2}{2}=21.15^\circ{\rm C}
\]
理论声速计算公式:
\[v_t = 331.45\sqrt{1+\frac{t'}{273.15}}
\]
代入:
\[v_t = 331.45\sqrt{1+\frac{21.15}{273.15}}
=344.3\;{\rm m/s}
\]
驻波法相对误差:
\[\delta = \frac{|v-v_t|}{v_t}
= \frac{|355.6-344.3|}{344.3}
=0.0328 \approx 3.28\%
\]
2. 李萨如图形频率测量
实验记录如下:
| $f_x$/Hz | $N_x$ | $N_y$ | $f_y$/Hz |
|---|---|---|---|
| 25 | 2 | 4 | 25 |
| 75 | 6 | 4 | 75 |
| 100 | 4 | 2 | 100 |
| 200 | 8 | 2 | 200 |
根据公式:
\[\frac{\omega_y}{\omega_x}=\frac{N_y}{N_x}
\]
可计算出 B 通道频率均与标称一致,说明信号源输出稳定,结果可靠。
3. 行波法数据处理
行波法测量波长的原理为:
当接收端压电陶瓷换能器移动,使示波器显示两信号相位相差为 $\pi$时,移动距离满足:
\[\Delta x = \frac{\lambda}{2}
\]
实验位置数据如下:
| i | $x_i$/mm |
|---|---|
| 1 | 21.825 |
| 2 | 26.128 |
| 3 | 30.451 |
| 4 | 34.720 |
| 5 | 38.980 |
| 6 | 43.218 |
| 7 | 47.368 |
| 8 | 51.584 |
| 9 | 55.817 |
| 10 | 60.087 |
计算相邻差值(单位:mm):
| 区间 | $\Delta x_i$/mm |
|---|---|
| 1–2 | 4.303 |
| 2–3 | 4.323 |
| 3–4 | 4.269 |
| 4–5 | 4.260 |
| 5–6 | 4.238 |
| 6–7 | 4.150 |
| 7–8 | 4.216 |
| 8–9 | 4.233 |
| 9–10 | 4.270 |
取平均:
\[\overline{\Delta x}=4.252\,{\rm mm}
=4.252\times10^{-3}\,{\rm m}
\]
故波长:
\[\lambda = 2\overline{\Delta x}
=8.504\times10^{-3}\,{\rm m}
\]
行波法声速:
\[v = f\lambda
=4.116\times 10^{4}\times 8.504\times10^{-3}
=350.0\;{\rm m/s}
\]
行波法相对误差:
\[\delta = \frac{|350.0-344.3|}{344.3}
=0.0166\approx 1.66\%
\]
4. 两种方法结果比较
| 方法 | 声速 v (m/s) | 理论值 v_t (m/s) | 相对误差 |
|---|---|---|---|
| 驻波法 | 355.6 | 344.3 | 3.28% |
| 行波法 | 350.0 | 344.3 | 1.66% |
行波法误差更小,说明行波法受振幅衰减与驻波节点位置偏移影响更小,稳定性更好。
5. 误差分析
- 驻波法中 Vpp 随位置变化不完全对称,导致波节判断存在偏移。
- 换能器输出频率存在微小漂移,影响波长测量。
- 空气温度微小波动直接影响声速理论值计算。
- 标尺读数误差与人为读数误差会引入额外偏差。
七、结论
驻波法和行波法均可测得空气中的声速,实验结果与理论值接近,其中行波法精度更高。实验验证了机械波叠加、驻波形成、相位差判断等基本物理规律。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号