用四端法测量Fe-Cr-Al丝的电阻率

用四端法测量 Fe-Cr-Al 丝的电阻率

---

实验时间：2025/11/03

一、实验目的

1. 了解接触电阻在低阻测量中的影响；
2. 掌握四端测量法的原理与操作；
3. 学会计算金属导线的电阻率及分析测量误差。

---

二、实验仪器

• Fe-Cr-Al 合金丝（待测样品）
• 标准电阻（精度 0.1 级）
• 滑线电阻器（总电阻约 30 Ω）
• 稳压电源（额定电流约 3 A）
• 四位半数字万用表（精度 0.05 级）
• 螺旋测微器、米尺、导线、开关等

---

三、实验原理

在测量低阻时，导线连接和接触处常引入附加电阻，称为接触电阻，一般为几十毫欧到几毫欧量级。若采用两端法测量，总电阻为：

\[R' = R_x + R_1 + R_2 + R_c \]

其中 ( R_x ) 为样品电阻，( R_1、R_2 ) 为引线电阻，( R_c ) 为接触电阻。
当被测电阻仅为毫欧级时，上式中附加项将导致显著误差。

为消除此类影响，采用四端法（Kelvin 法) 测量。该方法将电流供给回路与电压测量回路分离，使电压表仅反映样品两点间的真实电势差。

---

1. 四端法的基本原理

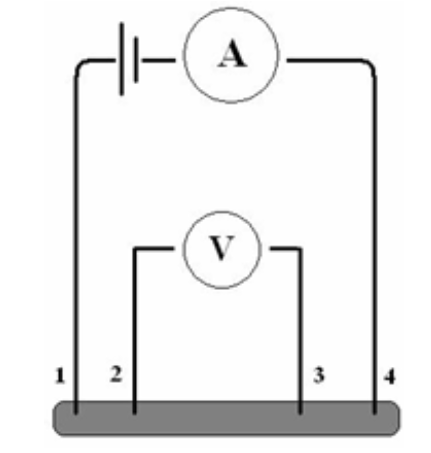
被测样品两端分别接入两组导线：

• 外侧端子 ( J, J' ) 供电流 ( I )；
• 内侧端子 ( P, P' ) 接电压表测电压 ( U )。

此时电压表测得的压降为样品的电势差：

\[R_s = \frac{U}{I} \]

由于电压表内阻远大于导线电阻，流经测量引线的电流极小，故可忽略压降影响，从而消除了接触电阻与引线电阻对结果的干扰。

---

2. 低值电阻的比较测量法

实验中常利用标准电阻与样品电阻串联，构成恒流或恒压电路，测量两者的电压比值来求未知电阻。
设标准电阻 ( R_n ) 两端电压为 ( U_n )，样品电压为 ( U_x )，电路电流为 ( I )，则：

\[I = \frac{U_n}{R_n} \]

代入$ ( R_s = \frac{U}{I} )$，可得：

\[R_s = \frac{U_x}{U_n} R_n \]

即样品电阻与标准电阻成比例关系。
当采用恒流源时，电流恒定；若使用恒压源，则应保证两端串联后电压分配适当，防止电流过大导致样品发热。

---

3. 电阻率计算

设样品长度为 ( L )，直径为 ( d )，横截面积：

\[S = \frac{\pi d^2}{4} \]

则其电阻率为：

\[\rho = R_s \frac{S}{L} = R_s \frac{\pi d^2}{4L} \]

将比较测得的 ( R_s ) 代入，可得：

\[\rho_s = \frac{\pi d^2 U_x R_n}{4L U_n} \]

式中各量均可实验测得，从而求出 Fe-Cr-Al 丝的电阻率。

---

4. 电阻率测量的不确定度估计

若各量的相对不确定度分别为 ( u_{U_x}, u_{U_n}, u_d, u_L, u_{R_n} )，则电阻率的综合相对不确定度为：

\[\frac{u_\rho}{\rho} = \sqrt{ \left(\frac{u_{U_x}}{U_x}\right)^2 + \left(\frac{u_{U_n}}{U_n}\right)^2 + \left(2\frac{u_d}{d}\right)^2 + \left(\frac{u_L}{L}\right)^2 + \left(\frac{u_{R_n}}{R_n}\right)^2 } \]

本实验主要误差来源于直径和电压测量。螺旋测微器的读数精度约为 0.01 mm，标准电阻及电压测量误差通常在 0.05 级左右，满足低阻测量的精度要求。

---

四、实验内容

1. 测量金属丝在不同位置的直径（6 次取平均）；
2. 测量导线的有效长度；
3. 按电路图连接标准电阻与样品，测两者电压并记录；
4. 改变电源电压重复测量，绘制 ( U_x )–( U_n ) 关系；
5. 计算 ( R_s ) 与电阻率 ( \rho )，并估算相对不确定度。

五、原始数据

测量项目	测量值	单位	备注
螺旋测微器读数	3.955, 3.911, 3.920, 3.929, 3.915, 3.914	mm	初读数 −0.030 mm，仪器误差 0.004 mm
米尺读数	42.02, 42.03, 42.02, 42.03, 42.02, 42.03	cm	仪器误差 0.5 mm
标准电阻电压 ( U_n )	36.11, 40.12, 44.84	mV
待测样品电压 ( U_x )	35.99, 40.08, 44.76	mV
标准电阻 ( R_n )	1.000 Ω（忘了）	—	作为计算参照

六、数据处理

计算

1. 导线直径平均值与修正

平均读数：

\[\bar{d} = \frac{3.955 + 3.911 + 3.920 + 3.929 + 3.915 + 3.914}{6} = 3.924\ \text{mm} \]

考虑初读数校正（−0.030 mm）：

\[d = \bar{d} - (-0.030) = 3.954\ \text{mm} \]

仪器修正后，导线平均直径为：

\[d = (3.954 \pm 0.004)\ \text{mm} \]

---

2. 导线长度平均值

平均读数：

\[\bar{L} = \frac{42.02 + 42.03 + 42.02 + 42.03 + 42.02 + 42.03}{6} = 42.025\ \text{cm} = 0.42025\ \text{m} \]

考虑米尺误差 ±0.0005 m：

\[L = (0.4203 \pm 0.0005)\ \text{m} \]

---

3. 计算样品电阻

根据比较法公式：

\[R_s = \frac{U_x}{U_n} R_n \]

计算三组结果：

组次	( U_x )(mV)	( U_n )(mV)	( R_s = \frac{U_x}{U_n} R_n )(Ω)
1	35.99	36.11	0.997
2	40.08	40.12	0.999
3	44.76	44.84	0.998

平均值：

\[\bar{R_s} = 0.998\ \Omega \]

---

4. 求横截面积

\[S = \frac{\pi d^2}{4} = \frac{\pi (3.954\times10^{-3})^2}{4} = 1.228\times10^{-5}\ \text{m}^2 \]

---

5. 计算电阻率

\[\rho = R_s \frac{S}{L} = 0.998 \times \frac{1.228\times10^{-5}}{0.4203} = 2.915\times10^{-5}\ \Omega\cdot\text{m} \]

结果：

\[\rho = (2.92 \pm \Delta\rho)\times10^{-5}\ \Omega\cdot\text{m} \]

---

不确定度

设相对不确定度由下式给出：

\[\frac{u_\rho}{\rho} = \sqrt{ \left(\frac{u_{U_x}}{U_x}\right)^2 + \left(\frac{u_{U_n}}{U_n}\right)^2 + \left(2\frac{u_d}{d}\right)^2 + \left(\frac{u_L}{L}\right)^2 + \left(\frac{u_{R_n}}{R_n}\right)^2 } \]

代入各项估值：

量	绝对误差	相对误差
( u_{U_x}, u_{U_n} )	0.05 mV	0.0012
( u_d )	0.004 mm	0.0010
( u_L )	0.5 mm	0.0012
( u_{R_n} )	0.0005 Ω	0.0005

则：

\[\frac{u_\rho}{\rho} = \sqrt{ (0.0012)^2 + (0.0012)^2 + (2\times0.0010)^2 + (0.0012)^2 + (0.0005)^2 } = 0.0029 \]

即：

\[u_\rho = 0.0029 \rho = 8.5\times10^{-8}\ \Omega\cdot\text{m} \]

---

最终结果

\[\rho = (2.92 \pm 0.01)\times10^{-5}\ \Omega\cdot\text{m} \]

与文献值$ ( (2.8\text{–}3.0)\times10^{-5}\ \Omega\cdot\text{m} ) $基本一致，说明实验精度良好，四端法有效消除了接触电阻对低阻测量的影响。

采用更高精度的电压采样与恒流源控制可进一步提高结果稳定性。