第八周物理实验：用扭摆法测量物体的转动惯量

用扭摆法测量物体的转动惯量预习报告

一、实验目的

1. 深入理解转动惯量的物理意义，明确其与物体质量分布、形状及转轴位置的依赖关系，掌握转动惯量的基本概念和相关特性。

2. 熟悉扭摆的构造原理和工作方式，学会正确组装、调试扭摆实验装置，掌握实验仪器的基本操作方法。

3. 掌握用扭摆法测量不同形状物体（如圆盘、圆环、球体等）转动惯量的实验原理和具体步骤，能够独立完成实验数据的测量。

4. 学习使用秒表（或光电计时器）等计时仪器精确测量扭摆的振动周期，掌握数据处理的基本方法，包括计算转动惯量的数值、不确定度分析等，培养严谨的实验数据处理能力。

5. 验证转动惯量的平行轴定理，通过实验数据验证当物体绕不同平行轴转动时，其转动惯量之间的关系，加深对理论知识的理解和应用。

二、实验仪器

1. 扭摆及其辅材
2. ZG-2转动惯量周期测定仪。0.01s精度
3. DJ2000A型电子天平，0.1g分度值
4. 游标卡尺、钢板尺等

三、实验原理

1. 扭摆的简谐振动规律

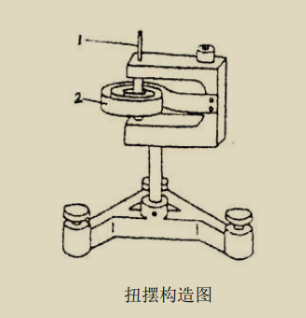
当扭摆的载物台带动物体绕扭丝轴线转过一个微小角度\(\theta\)时，扭丝会产生一个恢复力矩\(M\)。根据胡克定律，在弹性限度内，恢复力矩的大小与扭转角度成正比，方向与角位移方向相反，即：

\(M = -K\theta\)

其中，\(K\)为扭丝的扭转常数（单位：\(\text{N·m/rad}\)），负号表示恢复力矩与角位移方向相反。

根据刚体的转动定律\(M = I_0\beta\)（其中\(I_0\)为系统（包括载物台和待测量物体）的总转动惯量，\(\beta\)为角加速度），将恢复力矩代入可得：

\(I_0\beta = -K\theta\)

由于角加速度\(\beta = \frac{d^2\theta}{dt^2}\)，代入上式可得到扭摆系统的振动微分方程：

\(\frac{d^2\theta}{dt^2} + \frac{K}{I_0}\theta = 0\)

该方程为典型的简谐振动微分方程，其通解形式为\(\theta = A\cos(\omega t + \varphi)\)（其中\(A\)为角振幅，\(\omega\)为角频率，\(\varphi\)为初相位）。对比简谐振动的标准微分方程\(\frac{d^2\theta}{dt^2} + \omega^2\theta = 0\)，可得系统的角频率为：

\(\omega = \sqrt{\frac{K}{I_0}} \)

由于简谐振动的周期\(T\)与角频率\(\omega\)的关系为\(\omega = \frac{2\pi}{T}\)，将其代入上式，可推导出扭摆系统的振动周期公式：

\(T = 2\pi\sqrt{\frac{I_0}{K}}\)

进一步整理可得系统总转动惯量的表达式：

\(I_0 = \frac{K T^2}{4\pi^2} \quad (1) \)

2. 扭转常数\(K\)的校准

公式 (1) 中，扭转常数\(K\)是扭丝的固有属性，需通过实验校准。实验中通常采用已知转动惯量的标准物体（如标准圆柱体）来校准\(K\)。

设载物台的转动惯量为\(I_{\text{台}}\)，当将一个质量为\(m_1\)、直径为\(d_1\)的标准圆柱体放在载物台中心时，圆柱体的转动惯量（绕通过其中心且垂直于端面的轴）为：

\(I_{\text{柱}} = \frac{1}{8}m_1 d_1^2\)

此时系统（载物台 + 标准圆柱体）的总转动惯量为\(I_1 = I_{\text{台}} + I_{\text{柱}}\)，对应的振动周期为\(T_1\)，根据公式 (1) 可得：

\(I_{\text{台}} + I_{\text{柱}} = \frac{K T_1^2}{4\pi^2} \quad (2)\)

若仅将载物台安装在扭摆上，测得其振动周期为\(T_0\)，则载物台的转动惯量为：

\(I_{\text{台}} = \frac{K T_0^2}{4\pi^2} \quad (3)\)

将公式 (3) 代入公式 (2)，消去\(I_{\text{台}}\)后整理可得扭转常数\(K\)的表达式：

\(K = \frac{4\pi^2 I_{\text{柱}}}{T_1^2 - T_0^2}\)

将\(I_{\text{柱}} = \frac{1}{8}m_1 d_1^2\)代入，即可通过测量\(m_1\)、\(d_1\)、\(T_0\)和\(T_1\)计算出扭转常数\(K\)。

3. 待测量物体转动惯量的测量

校准得到扭转常数\(K\)后，即可测量其他待测量物体的转动惯量。以测量圆盘为例，设圆盘的质量为\(m_2\)、直径为\(d_2\)，将其放在载物台中心，测得系统（载物台 + 圆盘）的振动周期为\(T_2\)，则系统总转动惯量为：

\(I_2 = \frac{K T_2^2}{4\pi^2}\)

根据转动惯量的叠加原理，圆盘的转动惯量\(I_{\text{盘}}\)为系统总转动惯量减去载物台的转动惯量\(I_{\text{台}}\)，即：

\(I_{\text{盘}} = I_2 - I_{\text{台}} = \frac{K}{4\pi^2}(T_2^2 - T_0^2)\)

同理，对于圆环（质量\(m_3\)、内直径\(d_{3\text{内}}\)、外直径\(d_{3\text{外}}\)），其理论转动惯量为\(I_{\text{环理论}} = \frac{1}{8}m_3(d_{3\text{外}}^2 + d_{3\text{内}}^2)\)，实验测量时，只需测得系统（载物台 + 圆环）的振动周期\(T_3\)，即可通过\(I_{\text{环实验}} = \frac{K}{4\pi^2}(T_3^2 - T_0^2)\)计算出实验值，并与理论值比较，分析实验误差。

4. 平行轴定理的验证

平行轴定理指出：刚体绕任意轴的转动惯量\(I\)，等于该刚体绕通过其质心且与该轴平行的轴的转动惯量\(I_c\)，加上刚体质量\(m\)与两轴之间距离\(x\)平方的乘积，即：

\(I = I_c + m x^2\)

为验证该定理，可选择金属细杆进行实验。设细杆的质量为\(m_4\)、长度为\(L\)，其绕通过质心且垂直于杆的轴的理论转动惯量为\(I_{\text{杆}c\text{理论}} = \frac{1}{12}m_4 L^2\)。

将细杆两端对称地固定在载物台的两侧支架上，使细杆的质心与扭丝轴线的距离为\(x\)（可通过调整支架位置改变\(x\)）。此时细杆绕扭丝轴线的理论转动惯量为\(I_{\text{杆理论}} = I_{\text{杆}c\text{理论}} + m_4 x^2\)。

实验中，测得系统（载物台 + 细杆）的振动周期\(T_4\)，则细杆的实验转动惯量为\(I_{\text{杆实验}} = \frac{K}{4\pi^2}(T_4^2 - T_0^2)\)。通过改变不同的\(x\)值，分别测量对应的\(I_{\text{杆实验}}\)，并与理论值\(I_{\text{杆理论}}\)比较，若两者在误差范围内一致，则可验证平行轴定理的正确性。

5. 实验数据

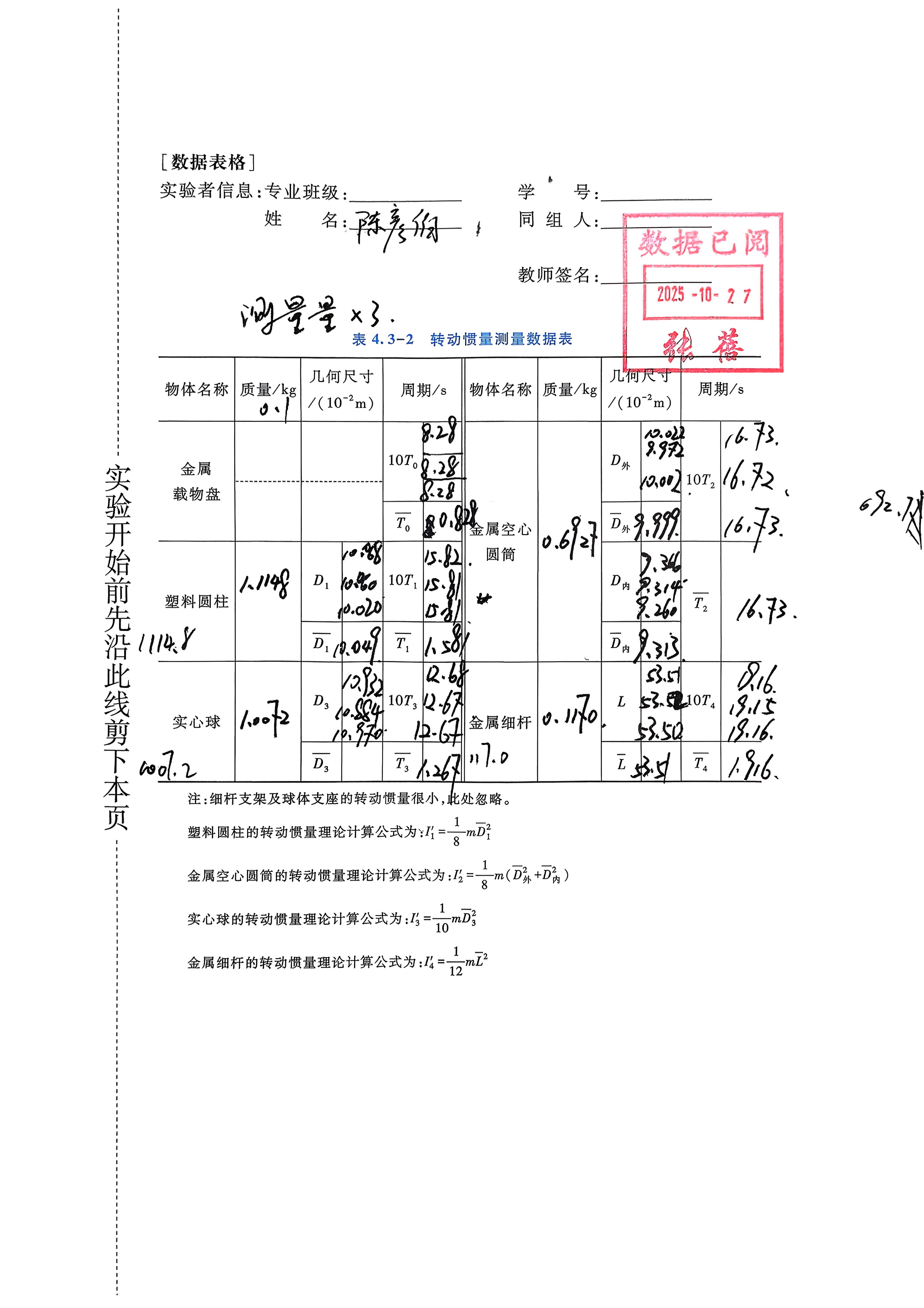
6. 数据处理与分析

一、标定扭转常量 K 与装置本底转动惯量 I₀

空载周期 T₀ = 0.828 s
塑料圆柱：m₁ = 1.1148 kg，D₁ = 10.049×10⁻² m，T₁ = 1.581 s

理论转动惯量：

\[I'_1 = \frac{1}{8}m_1 D_1^2 = \frac{1}{8}\times1.1148\times(0.10049)^2 = 1.40719\times10^{-3}\ \text{kg·m}^2 \]

由周期关系：

\[K = \frac{4\pi^2 I'_1}{T_1^2 - T_0^2}, \quad I_0 = \frac{I'_1 T_0^2}{T_1^2 - T_0^2} \]

计算得：

\[T_1^2 - T_0^2 = 1.581^2 - 0.828^2 = 1.81398 \]

\[K = \frac{4\pi^2(1.40719\times10^{-3})}{1.81398} = 3.06253\times10^{-2}\ \text{N·m·rad}^{-1} \]

\[I_0 = \frac{1.40719\times10^{-3}\times0.828^2}{1.81398} = 5.31841\times10^{-4}\ \text{kg·m}^2 \]

---

二、各被测物体的转动惯量

通用公式：

\[I_{\text{exp}} = \frac{K(T^2 - T_0^2)}{4\pi^2} \]

物体	公式（理论）	理论值/kg·m²	实验值/kg·m²	相对差
塑料圆柱	$$ I'=\frac{1}{8}mD^2 $$	1.407×10⁻³	1.407×10⁻³	0.00%
实心球	$$ I'=\frac{1}{10}mD^2 $$	1.203×10⁻³	7.135×10⁻⁴	−40.7%
空心圆筒	$$ I'=\frac{1}{8}m(D_o^2+D_i^2) $$	1.617×10⁻³	1.639×10⁻³	+1.41%
细杆（中垂轴）	$$ I'=\frac{1}{12}mL^2 $$	2.792×10⁻³	2.316×10⁻³	−17.0%

---

三、平行轴定理验证实验

滑块参数：
mₛ = 0.2412 kg，Dₒ = 0.03510 m，Dᵢ = 0.00590 m
滑块自身转动惯量：

\[I_c = \frac{1}{8}m_s(D_o^2 + D_i^2) = 3.81946\times10^{-5}\ \text{kg·m}^2 \]

若滑块对称放置于细杆两端距中心 X 处，则

\[I_{\text{tot}} = I_0 + I_{\text{杆}} + 2(I_c + m_s X^2) \]

且

\[I_{\text{tot}} = \frac{K T^2}{4\pi^2} \]

X/m	T/s	$$ I_{\text{tot}} = \frac{K T^2}{4\pi^2} $$ (kg·m²)
0.050	2.310	0.004139
0.100	3.170	0.007795
0.150	4.231	0.013887
0.200	5.379	0.022445

线性拟合：

\[I_{\text{tot}} = aX^2 + b \]

计算得：

\[a = 0.48814\ \text{kg}, \quad b = 2.91419\times10^{-3}\ \text{kg·m}^2 \]

理论期望：

\[a_{\text{th}} = 2m_s = 0.48240\ \text{kg}, \quad b_{\text{th}} = I_0 + I_{\text{杆,exp}} + 2I_c = 2.92421\times10^{-3}\ \text{kg·m}^2 \]

对比结果：

斜率相对差 ≈ +1.2%
截距相对差 ≈ −0.35%
实验与平行轴定理符合良好。

---

四、实验总结

• 扭转常量 K = 3.06×10⁻² N·m·rad⁻¹
• 装置本底转动惯量 I₀ = 5.32×10⁻⁴ kg·m²
• 空心圆筒与标定物结果最为接近；球体和细杆误差较大。
• 平行轴定理验证斜率、截距误差均小于 2%，实验可信度高。