第七周物理实验：分光仪调节及三棱镜折射率测量

分光仪调节及三棱镜折射率测量
时间：20251020

1. 实验目的

掌握分光仪调节和使用
测量三棱镜顶角
测量最小偏向角&玻璃折射率

2. 实验仪器

JJY型分光仪、双平面反射镜、玻璃三棱镜、汞灯

3. 实验原理

分光仪

主要组成部分：自由准直望远镜、平行光管、载物台、刻度盘、游标盘
自准直望远镜：观察和确定平行光方向。
平行光管：产生平行光束。
刻度盘/游标盘：29：30，精细到1’
调节要求：
狭缝必须处于平行光管透镜的焦平面上，由平行光管射出的光是平行光束
望远镜必须聚焦于平行光束，使射入望远镜的平行光会聚焦在望远镜的分划板十字线平面上，即成为共焦光学系统。
望远镜光轴和平行光管光轴都严格垂直于仪器主轴，转动望远镜时，其光轴扫过的平面精确地平行于刻度盘表面
分光仪测量三棱镜材料折射率
一束平行单色光从折射率n1介质入射到n2介质时，光会发生反射和折射。入射角θ1、折射角θ2和反射角θ3之间的关系满足光的折射定律（斯涅耳定律）：
θ1=θ3,n2sinθ2=n1sinθ1
三棱镜模型：

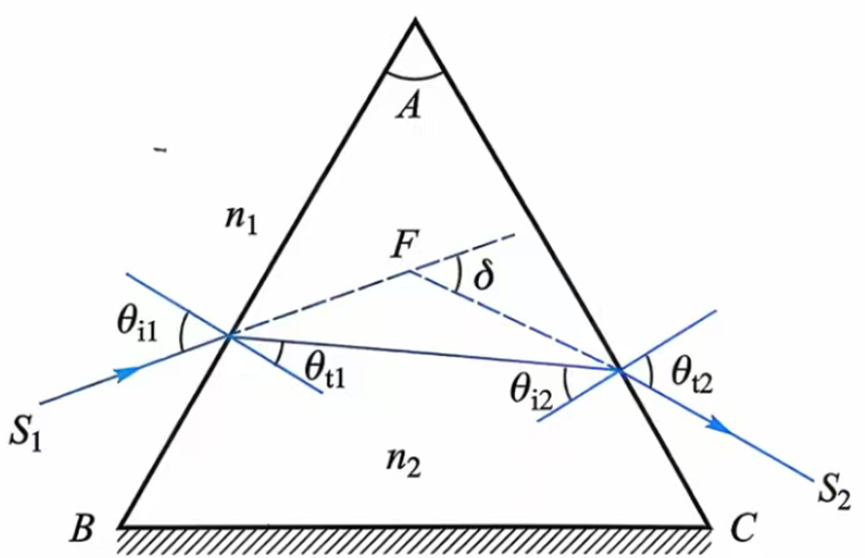
S1为入射光线，δ称为偏向角，满足：
δ=θi1-θt1+θt2-θi2=(θi1+θt2)-(θt1+θi2)
随入射角θi1变化，δ变化，δ存在最小值——最小偏向角δmin，此时有：
θi1=θt2,θt1=θi2
n2/n1=(sin 1/2(A+δmin))/(sin 1/2 A)
当棱镜置于空气中时，有n1=1，从而有：
n2=(sin (A+δmin)/2)/(sin A/2)
通过分光仪可以测得δmin和顶角A，从而计算得到棱镜对该单色光的折射率n2

自准法测量三棱镜顶角A

所谓自准法就是利用具有自准目镜的望远镜自身的平行光，射出望远镜的物镜后被平面镜(或三棱镜的反射面)反射回来。用自准法测量三棱镜顶角的方法如图4.17-11所示。将分光仪调节好后，打开目镜照明系统，将三棱镜放置在载物台上，用望远镜对准三棱镜的一个光学平面，使反射回来的绿十字像垂直线与分划板十字线的垂直线重合，记下望远镜的角位置(P1，P1’)。再将望远镜转到与另一光学面垂直的位置，使反射回来的绿十字像垂直线与分划板十字线的垂直线重合，记下望远镜的角位置(P2，P2’)。望远镜转过的角度|P1-P2|或|P1’-P2’|，就是三棱镜顶角的补角，即：
A=180°-(|P1-P2|+|P1^'-P2'|)/2

测量最小偏向角

对于材质、顶角一定的三棱镜，单色平行光射人棱镜时，其最小偏向角是唯一的。望远镜要跟着折射的绿色亮线转动,使绿色亮线不离开望远镜视场。当载物台转到某一位置时,再转动载物台,无论是向左转或是向右转,绿色亮线都是向离开人射线的方向移动,即向偏向角增大的方向移动,这个位置即最小偏向角的位置。反复实验,找出绿色亮线移动方向发生转折的确切位置,然后转动望远镜使绿色亮线与分划板垂直线重合,记下此时望远镜的角位置读数(P1,P1’)。然后用同样的方法找出最小偏向角的位置,记下此时望远镜的角位置读数(P2,P2’),这种方法测量的转角是2倍最小偏向角,因此有:
δmin=1/2(1/2 |P1-P2|+1/2|P1^'-P2'|)

4. 实验内容

实验内容与测量

调节分光仪，调节三棱镜，测量
测量结果：

数据处理与分析

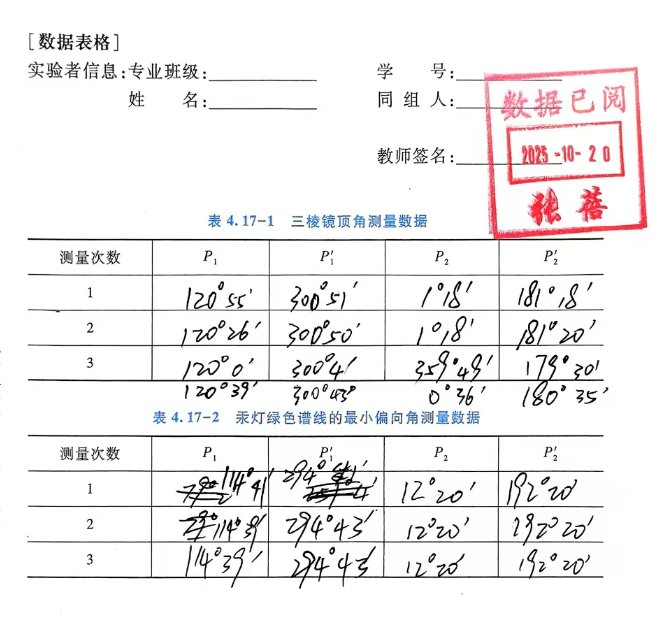
三棱镜顶角测量数值:

次数	A
1	60°41’
2	59°
3	59°14’
EVERAGE	59°38’

最小偏向角测量数值：

次数	δmin
1	51°10’
2	51°10’
3	51°10’
EVERAGE	51°10’

5. 数据处理

5.1. 角度测量与A类不确定度

物理量	原始数据（°′）	十进制度/°	平均值/°	A类不确定度 u_A/°
顶角 A	60°41′, 59°00′, 59°14′	60.6833, 59.0000, 59.2333	59.6389	0.53
最小偏向角 δmin（绿光）	51°10′（三次重合）	51.1667	51.1667	0.00

5.2. 仪器B类不确定度

双游标分光计最小分度 1′，按均匀分布估算：
u_B = 1′/√3 ≈ 0.01°。

5.3. 合成标准不确定度

u_c(A) = √(0.53² + 0.01²) ≈ 0.53°
u_c(δ_min) = 0.01°

5.4. 折射率计算

公式：
n = sin[(A + δ_min)/2] / sin(A/2)

代入 A = 59.6389°, δ_min = 51.1667°：
n = sin(55.4028°)/sin(29.8195°) = 0.8225 / 0.4970 ≈ 1.655

5.5. 折射率不确定度传播

灵敏度系数（弧度单位）：

• ∂n/∂A = –0.875 rad⁻¹
• ∂n/∂δ_min = 0.572 rad⁻¹

合成标准不确定度：
u_c(n) = √[(–0.875×0.0093)² + (0.572×0.00017)²] ≈ 0.008

最终结果：
n = 1.655 ± 0.008（k = 1，置信概率≈68%）

6. 分析

1. 不确定度来源

   • 顶角测量重复性差是主要贡献项，A 类分量达 0.53°，远大于仪器分辨力。
   • 最小偏向角三次读数完全一致，说明人眼判读误差与仪器分辨力相当，A 类分量为零，不确定度降至 0.01°。

2. 对折射率的影响
   敏感度系数显示，顶角不确定度对 (n) 的影响约为偏向角的 1.5 倍，故即使 (\delta_{\min}) 精度高，(A) 的分散性仍使 (u(n)) 达到 0.008。

3. 与文献值比较
   普通光学玻璃对 546 nm 绿光的标称折射率约 1.65–1.66，本次测量值 1.655 落在预期区间，偏差小于 0.5%，说明测量方案合理，但重复性有待改善。

---

---

7. 总结

1. 通过分光计测定三棱镜顶角与最小偏向角，获得了绿光折射率 (n=1.655\pm 0.008)，与文献值吻合。
2. 顶角测量的重复误差是扩展不确定度的主要来源；后续实验可采取多次独立调焦、对称游标取平均、改进对准方法等措施降低 A 类分量。
3. 最小偏向角判定需更精细的“左右逼近”找极值，以充分利用仪器分辨力。
4. 本实验验证了“最小偏向角法”测定折射率的可行性，同时量化了各误差源的贡献，为后续光谱分析、色散曲线测量提供了精度依据。