动态规划从精通到入门

前言

本文并非设计给 \(dp\) 入门选手，请注意。

本文将在笔者退役前持续更新，可能会有大量例题。

经典设计

[JSOI2011] 柠檬
使用特殊性质将不优情况剪去，将转移状态减少。

[CSP-S2019] Emiya 家今天的饭
储存将差分数组设计进 \(dp\) 状态中。

[UOI 2024]Heroes and Monsters

1. \(dp(i,j)\) 表示考虑到第 \(i\) 选了 \(j\) 个的方案数。
2. 将问题转化为固定转移方案可以使用多项式级别的动态规划

K-Kaleidoscope
考虑 \(dp\) 的过程类似找子序列的过程，将限制转化为位置集合限制。

[HAOI2015] 树上染色
树上问题，路径问题考虑边的转移次数，解决后效性。

[ABC416f]Paint Tree 2
逐个考虑，状态 \(0/1\) 表示是否可以继续转移。

[NOIP2022] 建造军营
把关键点集看做虚树，强制在虚树的根上统计答案（强制与其父亲的连边不能作为关键边）。

[NOIP2021] 方差
当全局增量难求时，可考虑插入的变量对所选集合的增量。

[USACO13OPEN] Photo G
将大体 \(dp\) 转移写出后为 \(f_i=f_j+1\) 的形式，刻画 \(j\) 的可能位置即可。

[ZSHOI-R1] 巡城
考虑求 \(dfn\) 序的期望值相当于求有多少个点在它前面的期望值。
遍历一棵树就要遍历完，算一棵有根树的贡献，它的子树内的点无影响，祖先一定有贡献。
考虑其他点的贡献，只有 \(\frac{1}{2}\) 的贡献（因为每个点对谁在前面的概率是相同的）。
考虑联通块间的贡献，为 \(\frac{v_y siz_y}{v_x+v_y}\)，\(v\) 的种类为 \(O(\sqrt{n})\)，暴力统计即可。

Sets of Complementary Sums
发现难以刻画集合是否合法，考虑由 \(a_i\) 的选择推到合法集合数。
由于 \(a_i\) 可重，容易发现重复元素的影响为全局加 \(a_i\)，差分数组不变。
考虑所有合法的差分数组。
考虑要刻画出极小的差分数组，所以最小的 \(a_i\) 一定是一。
又由于重复元素为全局加，所以每次都全局加一最优。
将问题转化为有至多 \(O(\sqrt{n})\) 个不可重数，和为 \(s\) 且 最小的 \(a_i\) 是一 的方案数 \(f_s\)。
答案为 \(\sum\limits_s f_s(n-s+1)\)。

优化状态

某模拟赛题
有 \(n \le 6\) 个非空，值域在 \([1, m] , m \le 300\) 的正整数集合。每个集合的元素互不相同，现在要从每一个集合中选出一个元素并求出它们的 \(\text {lcm}\)。你需要求出所有情况下的 \(\text {lcm}\) 的和。

有暴力 \(dp\)，将 \(lcm\) 记录到下标，枚举每个集合选哪个数即可。
状态数过多，考虑优化下标的 \(lcm\)。
将数分为两类，其中一类满足至多选一种数。但需要计算 \(lcm\) 的贡献，所以按最大质因数分类。
将最大质因数大于等于 \(17\) 的数分为一类即可。
状压，最后两边拼起来即可。

[POKATT 2024] 联合猫国 / The Paw-litical Game
在右端点处枚举所有合法极短区间。
发现只有所有子区间内答案为 \(1\) 的复杂度，在所有值相同时达到最大值 \(O(n\log{n})\)。

【MX-S6-T4】「KDOI-11」彩灯晚会
对于 \(\sum cnt_i^2\) 转化为选出两个长度为 \(l\) 颜色相同的链的方案数。
答案只需要知道恰好有 \(c\) 个重合的点即可统计。
考虑恰好转规定，然后二项式反演。
计算规定 \(c\) 个重合的点的方案。
\(dp(u,x,l_1,l_2)\) 表示两条链在 \(u\) 点重合，规定了 \(x\) 个重合点，有两条链分别有 \(l_1,l_2\) 个点时的方案数。
两条链相互独立，分步统计答案。

互不相关的两维状态 \(l_1,l_2\)，可以先转移 \(l_1\)，再转移 \(l_2\)。
时间复杂度 \(O(n^2 l^4)\)，还不够优秀。
将反演式子带回统计答案式子，用二项式定理化简后，发现每步转移乘一个 \(k-1\) 即可优化掉 \(x\) 这一维。
时间复杂度 \(O(n^2 l^3)\)。

Lonely King
首先有性质每个点的子树内至多有一个点可以上传，容易写出 \(O(n^2)\) 的暴力 \(dp\)。
将李超线段树合并优化斜率 \(dp\) 即可。

[NOI Online #1 入门组] 跑步（分拆数）
容易想出对每种数做一遍完全背包，时间复杂度 \(O(n^2)\) 不能接受。
由于大于 \(\sqrt{n}\) 的数不会超过 \(\sqrt{n}\) 个，考虑根号分治。
将大于临界的数加入，可以整体加一或插入一个最小值。
时间复杂度 \(O(n\sqrt{n})\)。

优化转移

[UOI 2024]Heroes and Monsters
不难想到当有 \(k\) 个成功和 \(n-k\) 个失败时。
最优方案为 \(a,b\) 排序后，成功的 \(a\) 依次和前 \(k\) 个 \(b\) 配对，失败的 \(a\) 依次和后 \(n-k\) 个 \(b\) 配对。

考虑枚举 \(k\)，记 \(dp(i,j)\) 表示考虑到前 \(i\) 个 \(j\) 个成功的方案数，容易转移，复杂度 \(O(n^3)\)。
考虑优化转移，对于每个 \(k\) 找到一个转移点.
转移点左边钦定 \(i\) 个成功，右边钦定 \(j\) 个失败，可以 \(O(n)\) 转移。
我们发现满足一个在 \(a\) 序列上找到左侧都小于 \(b_k\) 右侧都大于 \(b_k\) 的转移点即可。
它满足左边非成功的一定在右边失败，右边非失败的一定在左边成功。
前缀和输出即可，复杂度 \(O(n^2)\)。

[USACO20DEC] Sleeping Cows P
设计经典状态 \(dp(i,j)\) 表示前 \(i\) 个数中匹配了 \(j\) 个的方案数。
先排序，前面选完后可以直接算出当前可以填多少个位置。
由于可以不匹配完，考虑加一维状态表示还剩 \(k\) 个必须要匹配。
容易做到 \(O(n^3)\)。
考虑优化，将 \(k\) 这一维优化掉，类似上一题的，我们枚举分界点，考虑一个点前面的全部被选，这个点一定不选，限制出分界线，在前面选出 \(x\) 个点，在后面选出 \(i-x\) 的方案数，其它点可以随便选，乘一个阶乘即可。

[COCI 2007/2008 #1] ZAPIS
括号匹配与区间 \(dp\) 较符合，多段的转移可枚举第一段的长度来转移。

[POI 2011] TEM-Temperature
前缀的最值要想到单调队列。

ふたつの料理 (Two Dishes)
考虑朴素 \(O(n^2)dp\)。
不难写出 \(f(i,j)=\max{(f(i-1,j)+[j\le pa_i]va_i,f(i,j-1)+[i\le pb_j]vb_j)}\)。
考虑用数据结构优化掉第二维转移。
将 \(vb_i\) 容斥掉，先将答案加上 \(vb_i\)。
有 \(f'(i,j)=\max{(f(i-1,j)+[j\le pa_i]va_i,f(i,j-1))}-\sum_k [i=pb_k+1]vb_k\)
需要区间前缀 \(max\)，后缀加，\(map\) 维护差分即可。

\(bitset\) 优化 \(dp\)

\(bitset\) 可视为一个条件是否成立。
当转移形如 \(f(i,j)=[...][...]f(i-1,j)\) 时，
可以将 \([...]\) 用 \(bitset\) 来刻画，将三个 \(bitset\) 与起来即可。

闵可夫斯基和

[KOI 2025 #2] 序列与查询
\(ans=s+len*x\)，统计答案为标准的斜率优化形式，维护凸包即可。
瓶颈在计算长度为 \(len\) 的最大子段和。
实际上，我们不需要计算出其具体值，考虑序列分治直接维护凸包。
将两个序列合并的贡献为，左儿子的后缀凸包与右儿子的前缀凸包的 \((max,+)\) 卷积。
直接闵和，计入凸包贡献。
最后将整个凸包建出来即可。

\(wqs\) 二分优化 \(dp\)

对于一个凸性函数，我们可以二分斜率来切函数，使得消去题面上的恰好或至多（少）。
结论：费用流的最小费用是流量的凸函数（不会证，看 \(OI-wiki\) ）。

[八省联考 2018] 林克卡特树
首先简化题意，把 \(k\) 条边删去后为 \(k+1\) 个联通块，每个连通块选其最长链一定最优。
因此题意为选出树上恰好 \(k+1\) 条无交链，使得权值最大。
考虑 \(wqs\) 二分，拆点后可建模为费用流，有凸性成立。
\(dp(u,0/1)\) 表示 \(u\) 点能否继续向上转移即可。

不是 \(dp\)

[集训队互测 2024] 长野原龙势流星群
容易想出树上背包的 \(dp\) 转移。
考虑优化，转移形如 \((max,+)\) 卷积的形式，用启发式合并平衡树优化闵可夫斯基和可以做到 \(O(n\log^2{n})\)
如何做到 \(O(n\log{n})\)：
树上背包已经很难优化了，说明不是 \(dp\)。
这时考虑贪心，我们一定会先选数最大的一个点 \(x\) 单独作为联通块。
只要 \(x\) 的父亲被选，一定会选 \(x\)（因为 \(x\) 为目前最大）。
用并查集合并即可。

[USACO16OPEN] Landscaping P
每个位置是难以钦定 \(dp\) 顺序的。
我们有 减少一个土，增加一个土，两个土匹配 三种操作。
可以看出将每个位置的每个土当作一个点是容易 \(dp\) 的，拆点可以得到 \(O(n^2)\) 的 \(dp\)。

如果整体 \(dp\)，会发现难于 ふたつの料理 (Two Dishes)（我不会）。
思考是否存在性质，发现按位置配对，一定会匹配其 前驱或后继（或不配对）。
所以记录每个点的花费，\(cost_i=min{(X,Z(i-j) - cost_j)}\)，反悔贪心即可。

计数类

「CMOI R1」We Want To Run / Nilpotent
先转化题意，发现每个数只有 \(0\) 和非 \(0\) 两种本质不同的状态。
将矩阵转化为图的邻接矩阵，问题为原图是否有环，问题变为 \(DAG\) 计数。
设图 \(G\) 的最长链为 \(l(G)\)，边数为 \(e(G)\)。
则答案为 \(\sum\limits_{G} l(G)(a-1)^{e(G)}\)。
考虑使用 \(dp\) 优化计数。
可以按以点 \(u\) 结尾的最长链长度，将原图划为 \(l(G)\) 层依次 \(dp\)。
设 \(f(i,j,k)\) 为 \(dp\) 到第 \(i\) 层一共用了 \(j\) 个点，第 \(i\) 层有 \(k\) 个点的方案数。
枚举上一层节点数 \(p\)，不难写出：\(f(i,j,k)=\sum\limits_{p} f(i-1,j-k,p) \binom{j}{k} (a^p - 1)^k a^{k(j-k-p)}\)。
时间复杂度为 \(O(n^4)\)。

优化：
发现转移与 \(i\) 的关系不大，设 \(g(j,k)=\sum\limits_i f(i,j,k)\)，拆开后不难转移。
要统计答案，单独记一个 \(h(j,k)=\sum\limits_i i\ f(i,j,k)\) 即可。

连续段 \(dp\)

通常连续段 \(dp\) 用来解决 全排列 相关问题。
每次有 新开连通块，拼接在连通块两端，合并两个连通块 三种操作。
用连续段数来刻画 相对位置，最后合并成一个块即可得到 绝对位置。

[CEOI 2016] kangaroo
确定为连续段 \(dp\) 后，首先考虑转移顺序。
从小到大加入，分别考虑三种操作，新开和合并一定合法，拼接一定不合法，记录下有几个起（终）点即可。

[JOI Open 2016] 摩天大楼 / Skyscraper
是一种将连续段数设计进状态的一种 \(dp\) 方法。
用目前的连续段数（线头数）算出线长变化量来维护。

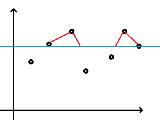
如下图，将三个线头延长（需记录终点、起点存在情况）。

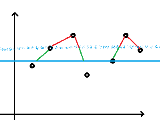
\(f(i,j)\) 表示考虑到前 \(i\) 个数时有 \(j\) 个连续段的方案数。
由于有起点终点会使后面转移减少一个线头，记一维 \(0/1/2\) 表示有几个端点。

[COCI 2021/2022 #2] Magneti
先看一个排列的方案数，设磁铁从左往右数，编号依次为 \(p_i\)。
将空位插板法插入 \(n+1\) 段，有方案数：

\[\binom{l-\sum\limits_i \max{(r_{p_i},r_{p_{i+1}})+n}}{n} \]

全排列问题考虑连续段 \(dp\)。
转移顺序，\(max\) 不好刻画，\(r\) 从小到大考虑，第 \(i\) 个元素贡献一定为 \(r_i\)，可以去掉 \(max\)。
\(dp\) 状态，要判断答案组合数上指标大于等于下指标，记录空位数。
\(f(i,j,k)\) 表示考虑到第 \(i\) 元素，连续段数为 \(j\)，\(\sum\) 为 \(k\) 的方案数。

某模拟赛题
令 \(\mathfrak{S}_n\) 为所有 \(n\) 阶排列构成的集合，计数：

\[\large\sum_{\pi\in\mathfrak{S}_n}\prod_{i=1}^{n-1}\left[a_{\pi(i)}a_{\pi(i+1)}\le C\right] \]

先考虑全正的情况。
钦定转移顺序，我们希望在转移的时候去掉条件的影响。
先从小向大填，如果一个数前面有限制，在第一次有限制之前插入。
需要注意的是，插入有限制的数时只能合并或作为序列端点。

考虑有负数时。
一个比较 \(naive\) 的想法是，由于正负间无限制，正负分别做上述内容，然后根据连续段数拼起来。
但是会算重。
思考后发现，是两个连通块拼起来也是合法的问题。
我们从大到小排序，使相邻两个联通块拼起来是不合法的，这样就不会算重了。
然后区别在于有限制的点只能新开一个连通块，不需要记录端点个数了。
正负拼起来即可。