剑指offer一刷:数学
剑指 Offer 39. 数组中出现次数超过一半的数字
难度:简单
方法一:哈希表统计法
遍历数组 nums,用 HashMap 统计各数字的数量,即可找出众数。此方法时间和空间复杂度均为 O(N)。
方法二:数组排序法
将数组 nums 排序,数组中点的元素一定为众数。
方法三:摩尔投票法
核心理念为票数正负抵消。此方法时间和空间复杂度分别为 O(N) 和 O(1),为本题的最佳解法。
详细如下:
设输入数组 nums 的众数为 x,数组长度为 n。
推论一:若记众数的票数为 +1,非众数的票数为 -1,则一定有所有数字的票数和 > 0。
推论二:若数组的前 a 个数字的票数和 = 0,则 数组剩余 (n-a) 个数字的票数和一定仍 >0,即后 (n-a) 个数字的众数仍为 x。
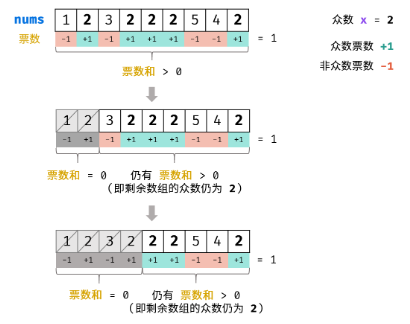
根据以上推论,记数组首个元素为 n1,众数为 x,遍历并统计票数。当发生票数和 = 0时,剩余数组的众数一定不变,这是由于:
- 当 n1 = x: 抵消的所有数字,有一半是众数 x。
- 当 n1 ≠ x: 抵消的所有数字,众数 x 的数量最少为 0 个,最多为一半。
利用此特性,每轮假设发生 票数和 = 0都可以缩小剩余数组区间。当遍历完成时,最后一轮假设的数字即为众数。
算法流程:
- 初始化:票数统计 votes = 0,众数 x;
- 循环:遍历数组 nums 中的每个数字 num;
- 当 票数 votes 等于 0,则假设当前数字 num 是众数;
- 当 num = x 时,票数 votes 自增 1;当 num != x 时,票数 votes 自减 1;
- 返回值:返回 x 即可;
class Solution {
public int majorityElement(int[] nums) {
int x = 0, votes = 0;
for(int num : nums){
if(votes == 0) x = num;
votes += num == x ? 1 : -1;
}
return x;
}
}
作者:Krahets
链接:https://leetcode.cn/leetbook/read/illustration-of-algorithm/99ussv/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。时间复杂度:O(N),空间复杂度:O(1)。
剑指 Offer 66. 构建乘积数组
难度:中等
本题难点在于不能使用除法。
我自己的做法是把乘积拆分成 B[i] 的左边和右边,构建 2 个累乘数组,对应相乘得到最终结果。
本质上和题解是一样的,题解是根据下面表格的主对角线(全为 1),将表格分为上三角和下三角两部分。分别迭代计算下三角和上三角两部分的乘积。

算法流程:
- 初始化:数组 B,其中 B[0] = 1;辅助变量 tmp = 1;
- 计算 B[i] 的下三角各元素的乘积,直接乘入 B[i];
- 计算 B[i] 的上三角各元素的乘积,记为 tmp,并乘入 B[i];
- 返回 B。
class Solution {
public int[] constructArr(int[] a) {
int len = a.length;
if(len == 0) return new int[0];
int[] b = new int[len];
b[0] = 1;
int tmp = 1;
for(int i = 1; i < len; i++) {
b[i] = b[i - 1] * a[i - 1];
}
for(int i = len - 2; i >= 0; i--) {
tmp *= a[i + 1];
b[i] *= tmp;
}
return b;
}
}
作者:Krahets
链接:https://leetcode.cn/leetbook/read/illustration-of-algorithm/570i11/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。时间复杂度:O(N),空间复杂度:O(1)(变量 tmp 使用常数大小额外空间,数组 b 作为返回值,不计入复杂度考虑)。
剑指 Offer 14- I. 剪绳子
难度:中等
给出以下两个推论,证明见题解
推论一:将绳子以相等的长度等分为多段,得到的乘积最大。
推论二:尽可能将绳子以长度 3 等分为多段时,乘积最大。
切分规则:
- 最优:3。把绳子尽可能切为多个长度为 3 的片段,留下的最后一段绳子的长度可能为 0, 1, 2 三种情况。
- 次优:2。若最后一段绳子长度为 2;则保留,不再拆为 1 + 1。
- 最差:1。若最后一段绳子长度为 1;则应把一份 3 + 1 替换为 2 + 2,因为 2 × 2 > 3 × 1。
算法流程:
- 当 n ≤ 3 时,按照规则应不切分,但由于题目要求必须剪成 m >1 段,因此必须剪出一段长度为 1 的绳子,即返回 n - 1。
- 当 n > 3 时,求 n 除以 3 的整数部分 a和余数部分 b(即 n = 3a + b ),并分为以下三种情况:
- 当 b = 0 时,直接返回 3a;
- 当 b = 1 时,要将一个 1 + 3 转换为 2 + 2,因此返回 3a-1 × 4;
- 当 b = 2 时,返回 3a × 2。
class Solution {
public int cuttingRope(int n) {
if(n <= 3) return n - 1;
int a = n / 3, b = n % 3;
if(b == 0) return (int)Math.pow(3, a);
if(b == 1) return (int)Math.pow(3, a - 1) * 4;
return (int)Math.pow(3, a) * 2;
}
}
作者:Krahets
链接:https://leetcode.cn/leetbook/read/illustration-of-algorithm/5vyva2/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。时间复杂度:O(1),空间复杂度:O(1)。
贪心算法见题解
另外,官方题解中还有动态规划解法,我刚开始想的也是动态规划,但是时间复杂度比较高(O(N2))
这里给出一个我看了官方题解中优化的动态规划解法的另一种思考(不一定对,主要是官方那个太难理解了。。):
首先,
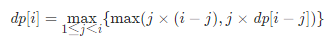
这个是普通的动态规划的方程。
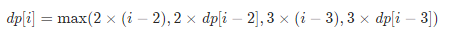
这个是优化的动态规划的方程。
2 × (i - 2) 和 3 × (i - 3) 暂且不谈。为什么只分成了 2 × dp[i - 2] 和 3 × dp[i - 3] 呢?
- dp[i] 必定 大于 1 × dp[i - 1],无需考虑该情况
- 4 × dp[i - 4] == 2 × 2 × dp[i - 4],而显然 dp[i - 2] ≥ 2 × dp[i - 4],所以该情况不需要考虑
- 5 × dp[i - 5] < 3 × 2 × dp[i - 5],而显然 dp[i - 3] ≥ 2 × dp[i - 5],所以该情况不需要考虑
- ……以此类推
所以只需要考虑 2 × dp[i - 2] 和 3 × dp[i - 3]。至于 2 × (i - 2) 和 3 × (i - 3) 主要是确保 i 比较小的时候(如 dp[3] = 2 < 3)能够不出错。
此时突然发现 i ≥ 7 后 2 × dp[i - 2] 也不需要算(根据前面数学解法的结果来看,无论余数是几,只要前面至少有一个 3,都可以除掉一个 3,由于余数一样,此时必然是 dp[i-3]):dp[7] = 3 × dp[4],dp[8] = 3 × dp[5],dp[9] = 3 × dp[6],dp[10] = 3 × dp[7],……。这其实已经接近数学的解法了,可以推导出数学公式了。这个时候算法流程就成了:
- i < 4,return i - 1;
- i = 4,return i;
- i > 4,给 dp[2] ~ dp[4] 分别赋值 2 ~ 4,然后 dp[i] = 3 × dp[i-3]。
进一步想,也不需要从 2 开始一个一个算到 i。先除以 3,看有几个 3 的幂,再求余,看是几,最后一综合(实质上就跟数学法完全一样了(⊙o⊙)…)
进一步想
剑指 Offer 57 - II. 和为 s 的连续正数序列
难度:简单
方法一:求和公式
设连续正整数序列的左边界 i 和右边界 j,则此序列的元素和 target等于元素平均值 (i + j) / 2乘以元素数量 (j - i + 1),即:
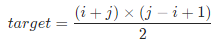
计算出 j 的唯一解求取公式为:
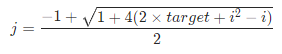
通过从小到大遍历左边界 i 来计算以 i 为起始数字的连续正整数序列。每轮中,由以上公式计算得到右边界 j,当 j 为整数时符合题目的连续正整数数列要求,此时记录结果即可。

class Solution {
public int[][] findContinuousSequence(int target) {
int i = 1;
double j = 2.0;
List<int[]> res = new ArrayList<>();
while(i < j) {
j = (-1 + Math.sqrt(1 + 4 * (2 * target + (long) i * i - i))) / 2;
if(j == (int)j) {
int[] ans = new int[(int)j - i + 1];
for(int k = i; k <= (int)j; k++)
ans[k - i] = k;
res.add(ans);
}
i++;
}
return res.toArray(new int[0][]);
}
}
作者:Krahets
链接:https://leetcode.cn/leetbook/read/illustration-of-algorithm/eth6p5/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。时间复杂度:O(N)(i < j,最多遍历 target/2 次),空间复杂度:O(1)。
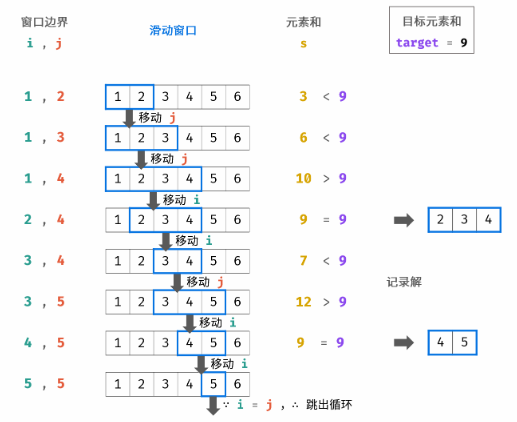
方法二:滑动窗口(双指针)
算法流程:
- 初始化:左边界 i = 1,右边界 j = 2,元素和 s = 3,结果列表 res;
- 循环:当 i ≥ j 时跳出;
- 当 s > target 时: 向右移动左边界 i = i + 1,并更新元素和 s;
- 当 s < target 时: 向右移动右边界 j = j + 1,并更新元素和 s;
- 当 s = target 时: 记录连续整数序列,并向右移动左边界 i = i + 1;
- 返回值:返回结果列表 res;
class Solution {
public int[][] findContinuousSequence(int target) {
int i = 1, j = 2, s = 3;
List<int[]> res = new ArrayList<>();
while(i < j) {
if(s == target) {
int[] ans = new int[j - i + 1];
for(int k = i; k <= j; k++)
ans[k - i] = k;
res.add(ans);
}
if(s >= target) {
s -= i;
i++;
} else {
j++;
s += j;
}
}
return res.toArray(new int[0][]);
}
}
作者:Krahets
链接:https://leetcode.cn/leetbook/read/illustration-of-algorithm/eth6p5/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。时间复杂度:O(N)(i < j,最多遍历 target 次,i、j 都移动到 target/2 处),空间复杂度:O(1)。
以上两种解法,考虑到解的稀疏性,将列表构建时间简化考虑为 O(1)。
注意最后的 res.toArray(new int[0][]),将列表转换成二维数组。
剑指 Offer 62. 圆圈中最后剩下的数字
难度:简单
模拟法需要循环删除 n - 1 轮,每轮在链表中寻找删除节点需要 m 次访问操作(链表线性遍历),因此总体时间复杂度为 O(nm)。
实际上,本题是著名的“约瑟夫环”问题,可使用动态规划解决。
输入 n, m,记此约瑟夫环问题为 「n, m 问题」 ,设解(即最后留下的数字)为 f(n),则有:
- 「n, m 问题」:数字环为 0, 1, 2, ..., n - 1,解为 f(n);
- 「n-1, m 问题」:数字环为 0, 1, 2, ..., n - 2,解为 f(n-1);
- 以此类推……
对于「n, m 问题」,首轮删除环中第 m 个数字后,得到一个长度为 n - 1 的数字环。由于有可能 m > n,因此删除的数字为 (m - 1) % n,删除后的数字环从下个数字(即 m % n)开始,设 t = m % n,可得数字环:
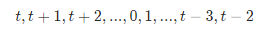
删除一轮后的数字环也变为一个「n-1, m 问题」,观察以下数字编号对应关系:

设「n-1, m 问题」某数字为 x,则可得递推关系:
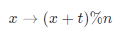
换而言之,若已知「n-1, m 问题」的解 f(n - 1),则可通过以上公式计算得到「n, m 问题」的解 f(n),即:
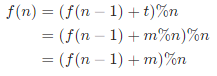
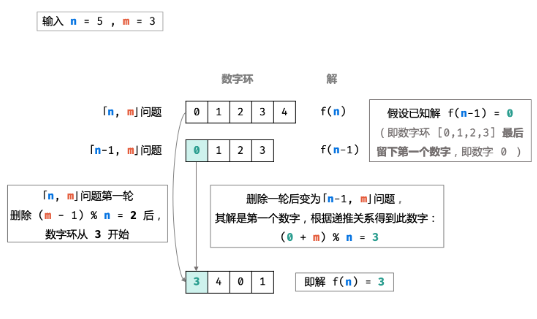
f(n) 可由 f(n - 1) 得到,f(n - 1) 可由 f(n - 2) 得到,……,f(2) 可由 f(1) 得到;因此,若给定 f(1) 的值,就可以递推至任意 f(n)。而「1, m 问题」的解 f(1) = 0 恒成立,即无论 m 为何值,长度为 1 的数字环留下的是一定是数字 0。
以上数学推导本质是得出动态规划的转移方程和初始状态。
动态规划解析:
- 状态定义:设「i, m 问题」的解为 dp[i];
- 转移方程:通过以下公式可从 dp[i - 1] 递推得到 dp[i];
- dp[i] = (dp[i - 1] + m) % i
- 初始状态:「1, m 问题」的解恒为 0,即 dp[1] = 0;
- 返回值:返回「n, m 问题」的解 dp[n];
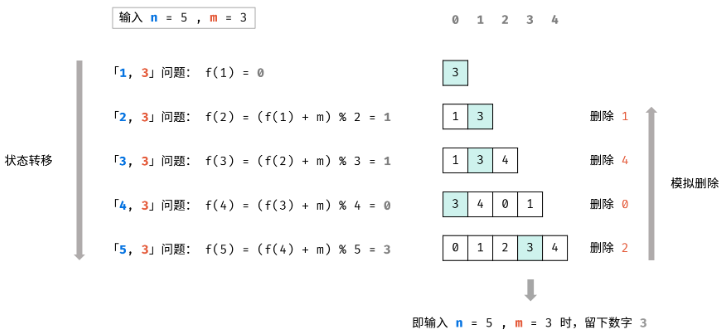
根据状态转移方程的递推特性,无需建立状态列表 dp,而使用一个变量 x 执行状态转移即可。
class Solution {
public int lastRemaining(int n, int m) {
int x = 0;
for (int i = 2; i <= n; i++) {
x = (x + m) % i;
}
return x;
}
}
作者:Krahets
链接:https://leetcode.cn/leetbook/read/illustration-of-algorithm/oxp3er/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。时间复杂度:O(N),空间复杂度:O(1)。
剑指 Offer 14- II. 剪绳子 II
难度:中等
此题与剪绳子 I 等价,具体原理不再介绍,主要介绍一下大数求余的解法。
大数求余解法:
大数越界:当 a 增大时,最后返回的 3a 大小以指数级别增长,可能超出 int32 甚至 int64 的取值范围,导致返回值错误。
大数求余问题:在仅使用 int32 类型存储的前提下,正确计算 xa 对 p 求余(即 xa ⊙ p)的值。
解决方案:循环求余、快速幂求余,其中后者的时间复杂度更低,两种方法均基于以下求余运算规则推出:
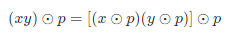
1. 循环求余:
- 根据求余运算性质推出
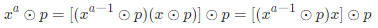
- 解析:利用此公式,可通过循环操作依次求 x1, x2, ..., xa-1, xa 对 p 的余数,保证每轮中间值 rem 都在 int32 取值范围中。
- 时间复杂度 O(N):其中 N = a,即循环的线性复杂度。
2. 快速幂求余:
- 根据求余运算性质可推出:
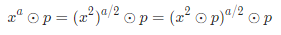
- 当 a 为奇数时 a/2 不是整数,因此分为以下两种情况(''//'' 代表向下取整的除法):
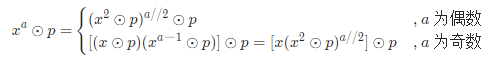
- 解析:利用以上公式,可通过循环操作每次把指数 a 问题降低至指数 a//2 问题,只需循环 log2(N) 次,因此可将复杂度降低至对数级别。
- 帮助理解:根据下表,初始状态 rem = 1, x = 3, a = 19, p = 1000000007,最后会将 rem × (xa ⊙ p) 化为 rem × (x0 ⊙ p) = rem × 1 的形式,即 rem 为余数答案。
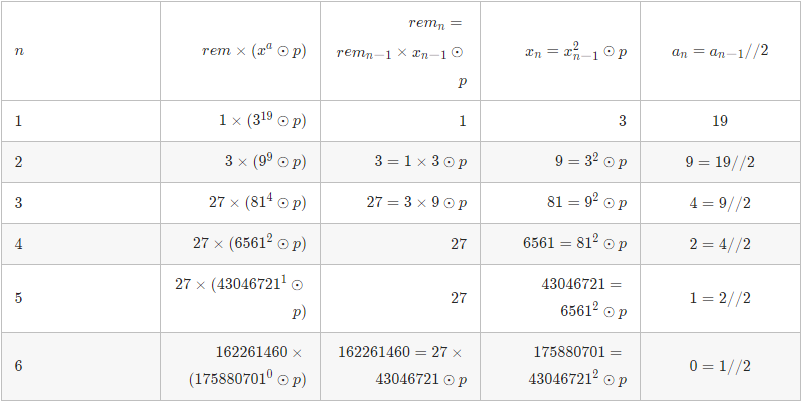
- 时间复杂度 O(log2N):其中 N = a,二分法为对数级别复杂度,每轮仅有求整、求余、次方运算。
根据二分法计算原理,至少要保证变量 x 和 rem 可以正确存储 10000000072,而 264 > 10000000072 > 232,因此我们选取 long 类型。
class Solution {
public int cuttingRope(int n) {
if(n <= 3) return n - 1;
int b = n % 3, p = 1000000007;
long rem = 1, x = 3;
for(int a = n / 3 - 1; a > 0; a /= 2) {
if(a % 2 == 1) rem = (rem * x) % p;
x = (x * x) % p;
}
if(b == 0) return (int)(rem * 3 % p);
if(b == 1) return (int)(rem * 4 % p);
return (int)(rem * 6 % p);
}
}
作者:Krahets
链接:https://leetcode.cn/leetbook/read/illustration-of-algorithm/5vbrri/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。剑指 Offer 43. 1~n 整数中 1 出现的次数
难度:困难
将 1 ~ n 的个位、十位、百位、...的 1 出现次数相加,即为 1 出现的总次数。
设数字 n 是个 x 位数,记 n 的第 i 位为 ni,则可将 n 写为 nxnx-1⋯n2n1;本文名词规定如下:
- 称「 ni 」称为当前位,记为 cur;
- 将「 ni-1ni-2⋯n2n1 」称为低位,记为 low;
- 将「 nxnx-1⋯ni+2ni+1 」称为高位,记为 high;
- 将「 10i 」称为位因子,记为 digit;
某位中 1 出现次数的计算方法:
根据当前位 cur 值的不同,分为以下三种情况:
- 当 cur = 0 时:此位 1 的出现次数只由高位 high 决定,计算公式为:high × digit
- 当 cur = 1 时:此位 1 的出现次数由高位 high 和低位 low 决定,计算公式为:high × digit + low + 1
- 当 cur = 2, 3, ⋯, 9 时:此位 1 的出现次数只由高位 high 决定,计算公式为:(high + 1) × digit
变量递推公式:
设计按照 “个位、十位、...” 的顺序计算,则 high / cur / low / digit 应初始化为:
int high = n / 10;
int cur = n % 10;
int low = 0;
int digit = 1; // 个位因此,从个位到最高位的变量递推公式为:
while(high != 0 || cur != 0) { // 当 high 和 cur 同时为 0 时,说明已经越过最高位,因此跳出
low += cur * digit; // 将 cur 加入 low ,组成下轮 low
cur = high % 10; // 下轮 cur 是本轮 high 的最低位
high /= 10; // 将本轮 high 最低位删除,得到下轮 high
digit *= 10; // 位因子每轮 × 10
}代码如下:
class Solution {
public int countDigitOne(int n) {
int digit = 1, res = 0;
int high = n / 10, cur = n % 10, low = 0;
while(high != 0 || cur != 0) {
if(cur == 0) res += high * digit;
else if(cur == 1) res += high * digit + low + 1;
else res += (high + 1) * digit;
low += cur * digit;
cur = high % 10;
high /= 10;
digit *= 10;
}
return res;
}
}
作者:Krahets
链接:https://leetcode.cn/leetbook/read/illustration-of-algorithm/57nyhd/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。时间复杂度:O(logN),空间复杂度:O(1)。
剑指 Offer 44. 数字序列中某一位的数字
难度:中等
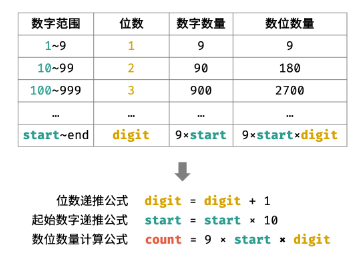
观察上表,可推出各 digit 下的数位数量 count 的计算公式:count = 9 × start × digit
根据以上分析,可将求解分为三步:
- 确定 n 所在数字的位数,记为 digit;
- 确定 n 所在的数字,记为 num;
- 确定 n 是 num 中的哪一数位,并返回结果;
1. 确定所求数位的所在数字的位数
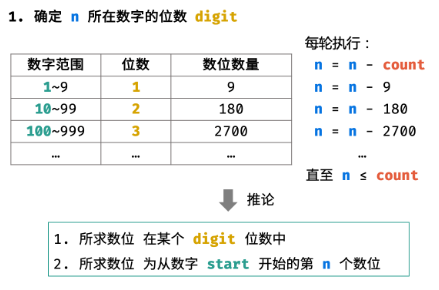
如下图所示,循环执行 n 减去 一位数、两位数、... 的数位数量 count,直至 n ≤ count 时跳出。
由于 n 已经减去了一位数、两位数、...、(digit−1) 位数的数位数量count,因而此时的 n 是从起始数字 start 开始计数的。
int digit = 1;
long start = 1;
long count = 9;
while (n > count) {
n -= count;
start *= 10; // 1, 10, 100, ...
digit += 1; // 1, 2, 3, ...
count = digit * start * 9; // 9, 180, 2700, ...
}结论:所求数位 ① 在某个 digit 位数中; ② 为从数字 start 开始的第 n 个数位。
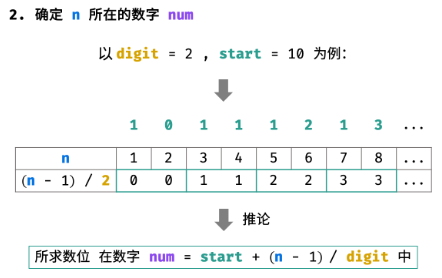
2. 确定所求数位所在的数字
如下图所示,所求数位 在从数字 start 开始的第 [(n - 1) / digit] 个数字中(start 为第 0 个数字)。
long num = start + (n - 1) / digit;结论:所求数位在数字 num 中。
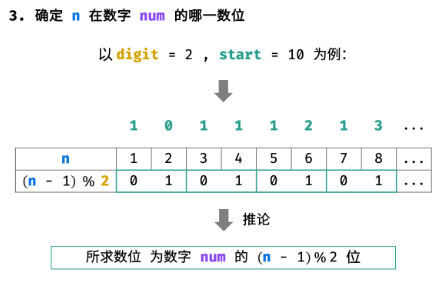
3. 确定所求数位在 num 的哪一数位
如下图所示,所求数位为数字 num 的第 (n - 1) % digit 位( 数字的首个数位为第 0 位)。
String s = Long.toString(num); // 转化为 string
int res = s.charAt((n - 1) % digit) - '0'; // 获得 num 的 第 (n - 1) % digit 个数位,并转化为 int结论:所求数位是 res。
class Solution {
public int findNthDigit(int n) {
int digit = 1;
long start = 1;
long count = 9;
while (n > count) { // 1.
n -= count;
start *= 10;
digit += 1;
count = digit * start * 9;
}
long num = start + (n - 1) / digit; // 2.
return Long.toString(num).charAt((n - 1) % digit) - '0'; // 3.
}
}
作者:Krahets
链接:https://leetcode.cn/leetbook/read/illustration-of-algorithm/57w6b3/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。时间复杂度:O(logN),空间复杂度:O(logN)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号