剑指offer一刷:位运算
剑指 Offer 15. 二进制中 1 的个数
难度:简单
方法一:逐位判断
算法流程:
- 初始化数量统计变量 res = 0。
- 循环逐位判断:当 n = 0 时跳出。
- res += n & 1:若 n & 1 = 1,则统计数 res 加一。
- n >>= 1:将二进制数字 n 无符号右移一位( Java 中无符号右移为 ">>>" ) 。
- 返回统计数量 res。
public class Solution {
public int hammingWeight(int n) {
int res = 0;
while(n != 0) {
res += n & 1;
n >>>= 1;
}
return res;
}
}
作者:Krahets
链接:https://leetcode.cn/leetbook/read/illustration-of-algorithm/5vgz7m/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。时间复杂度:O(log N),空间复杂度:O(1)。
方法二:巧用 n & (n - 1)

算法流程:
- 初始化数量统计变量 res。
- 循环消去最右边的 1:当 n = 0 时跳出。
- res += 1: 统计变量加 1;
- n &= n - 1: 消去数字 n 最右边的 1。
- 返回统计数量 res。
public class Solution {
public int hammingWeight(int n) {
int res = 0;
while(n != 0) {
res++;
n &= n - 1;
}
return res;
}
}
作者:Krahets
链接:https://leetcode.cn/leetbook/read/illustration-of-algorithm/5vgz7m/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。时间复杂度:O(M)(M 为二进制数字 n 中 1 的个数),空间复杂度:O(1)。
剑指 Offer 65. 不用加减乘除做加法
难度:简单
设两数字的二进制形式 a, b,其求和 s = a + b,a(i) 代表 a 的二进制第 i 位,则分为以下四种情况:
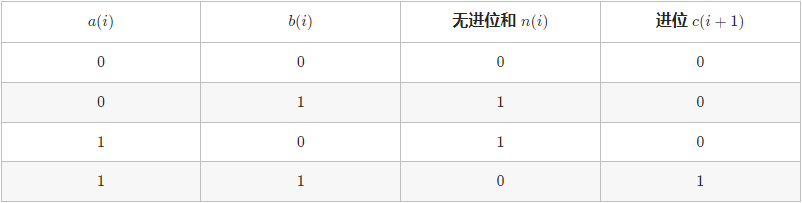
观察发现,无进位和与异或运算规律相同,进位和与运算规律相同(并需左移一位)。因此,无进位和 n 与进位 c 的计算公式如下:

(和 s)=(非进位和 n)+(进位 c)。即可将 s = a + b 转化为:
s = a + b ⇒ s = n + c
循环求 n 和 c ,直至进位 c = 0;此时 s = n,返回 n 即可。(∵补码,∴负数可以一样直接计算)
为了便于理解,给出以下形式
00001101 = 00000101 + 00001000
+ + +
00000111 = 00000101 + 00000010
|| || ||
00010100 = 00001010 + 00001010
此时左边第一列就是 a + b = s,最下面一行就是 s = c + n
左边第一列即原始的 2 个数相加得到最下面的数,而拆成右边两列,第一列为进位(2 个数相同),第二列为非进位和(2 个数的异或就是它们的和)。右边两列分别相加(即上述 n 和 c 的运算,并非直接相加),得到最下面的 2 个数,再把下面 2 个数作为后一个操作的第一列的上面 2 个数再进行这种形式的相加,直到最终使得第二列的最下面一个数(进位和)为 0,此时第三列的最下面一个数就是最终结果。
class Solution {
public int add(int a, int b) {
while(b != 0) { // 当进位为 0 时跳出
int c = (a & b) << 1; // c = 进位
a ^= b; // a = 非进位和
b = c; // b = 进位
}
return a;
}
}
作者:Krahets
链接:https://leetcode.cn/leetbook/read/illustration-of-algorithm/5vs8w7/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。时间复杂度:O(1)(最差情况循环 32 次),空间复杂度:O(1)。
剑指 Offer 56 - I. 数组中数字出现的次数
难度:中等
题目要求时间复杂度 O(N),空间复杂度 O(1),因此首先排除暴力法和哈希表统计法。
简化问题:一个整型数组 nums 里除一个数字之外,其他数字都出现了两次。
设整型数组 nums 中出现一次的数字为 x,出现两次的数字为 a, a, b, b, ...,即:
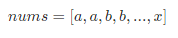
异或运算有个重要的性质,两个相同数字异或为 0,即对于任意整数 a 有 a ⊕ a = 0。因此,若将 nums 中所有数字执行异或运算,留下的结果则为出现一次的数字 x,即:
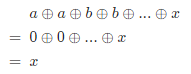
异或运算满足交换律 a ⊕ b = b ⊕ a,即以上运算结果与 nums 的元素顺序无关。
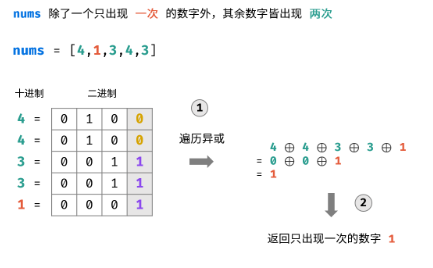
本题难点:数组 nums 有两个只出现一次的数字,因此无法通过异或直接得到这两个数字。
设两个只出现一次的数字为 x, y,由于 x ≠ y,则 x 和 y 二进制至少有一位不同(即分别为 0 和 1),根据此位可以将 nums 拆分为分别包含 x 和 y 的两个子数组。
易知两子数组都满足「除一个数字之外,其他数字都出现了两次」。因此,仿照以上简化问题的思路,分别对两子数组遍历执行异或操作,即可得到两个只出现一次的数字 x, y。
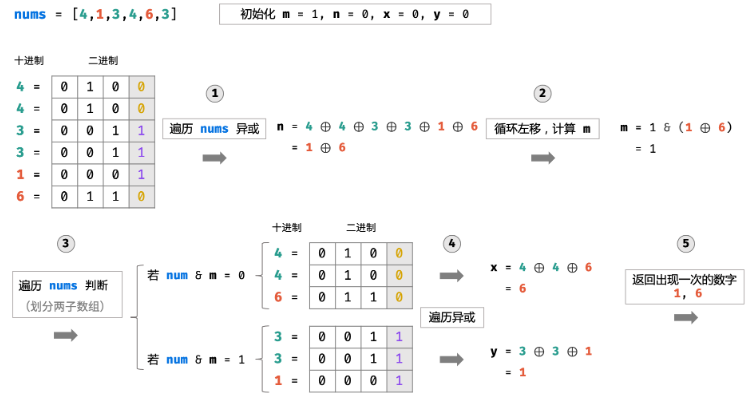
具体算法流程见题解
class Solution {
public int[] singleNumbers(int[] nums) {
int x = 0, y = 0, n = 0, m = 1;
for(int num : nums) // 1. 遍历异或
n ^= num;
while((n & m) == 0) // 2. 循环左移,计算 m
m <<= 1;
for(int num: nums) { // 3. 遍历 nums 分组
if((num & m) != 0) x ^= num; // 4. 当 num & m != 0
else y ^= num; // 4. 当 num & m == 0
}
return new int[] {x, y}; // 5. 返回出现一次的数字
}
}
作者:Krahets
链接:https://leetcode.cn/leetbook/read/illustration-of-algorithm/euj1a1/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。时间复杂度:O(N),空间复杂度:O(1)。
剑指 Offer 56 - II. 数组中数字出现的次数 II
难度:中等
方法一:有限状态自动机
具体见题解
方法二:遍历统计
(此方法相对容易理解,但效率较低,总体推荐方法一)
使用与运算,可获取二进制数字 num 的最右一位 n1:
n1 = num & i
配合右移操作,可从低位至高位,获取 num 所有位的值(设 int 类型从低至高的位数为第 0 位 至第 31 位,即 n0 ~ n31):
num = num >> 1
建立一个长度为 32 的数组 counts,通过以上方法可记录所有数字的各二进制位的 的出现次数之和。
int[] counts = new int[32];
for(int num : nums) {
for(int i = 0; i < 32; i++) {
counts[i] += num & 1; // 更新第 i 位 1 的个数之和
num >>= 1; // 第 i 位 --> 第 i + 1 位
}
}将 counts 各元素对 求余,则结果为“只出现一次的数字”的各二进制位。
利用左移操作和或运算,可将 counts 数组中各二进位的值恢复到数字 re 上。
for(int i = 31; i >= 0; i--) {
res <<= 1;
res |= counts[i] % 3; // 恢复第 i 位
}最终返回 re 即可。
整体代码如下:
class Solution {
public int singleNumber(int[] nums) {
int[] counts = new int[32];
for(int num : nums) {
for(int i = 0; i < 32; i++) {
counts[i] += num & 1; // 更新第 i 位 1 的个数之和
num >>= 1; // 第 i 位 --> 第 i 位
}
}
int res = 0, m = 3;
for(int i = 31; i >= 0; i--) {
res <<= 1;
res |= counts[i] % m; // 恢复第 i 位
}
return res;
}
}
作者:Krahets
链接:https://leetcode.cn/leetbook/read/illustration-of-algorithm/9hctss/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。时间复杂度:O(N),空间复杂度:O(1)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号