剑指offer一刷：分治算法

剑指 Offer 07. 重建二叉树

难度：中等

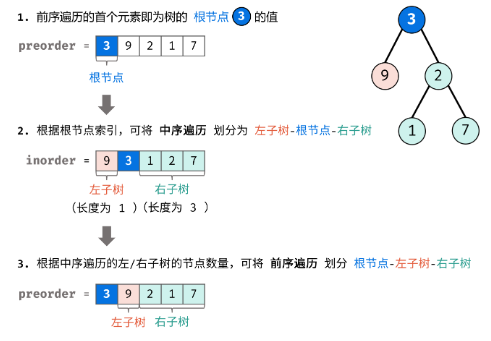
根据「分治算法」思想，对于树的左、右子树，仍可复用以上方法划分子树的左右子树。

分治算法解析：

• 递推参数：根节点在前序遍历的索引 root、子树在中序遍历的左边界 left、子树在中序遍历的右边界 right；
• 终止条件：当 left > right，代表已经越过叶节点，此时返回 null；
• 递推工作：
  • 建立根节点 node：节点值为 preorder[root]；
  • 划分左右子树：查找根节点在中序遍历 inorder 中的索引 i；为了提升效率，本文使用哈希表 dic 存储中序遍历的值与索引的映射，查找操作的时间复杂度为 O(1)；
  • 构建左右子树：开启左右子树递归；

• 返回值： 回溯返回 node，作为上一层递归中根节点的左 / 右子节点；

class Solution {
    int[] preorder;
    HashMap<Integer, Integer> dic = new HashMap<>();
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        this.preorder = preorder;
        for(int i = 0; i < inorder.length; i++)
            dic.put(inorder[i], i);
        return recur(0, 0, inorder.length - 1);
    }
    TreeNode recur(int root, int left, int right) {
        if(left > right) return null;                          // 递归终止
        TreeNode node = new TreeNode(preorder[root]);          // 建立根节点
        int i = dic.get(preorder[root]);                       // 划分根节点、左子树、右子树
        node.left = recur(root + 1, left, i - 1);              // 开启左子树递归
        node.right = recur(root + i - left + 1, i + 1, right); // 开启右子树递归
        return node;                                           // 回溯返回根节点
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/99ljye/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)（初始化哈希表、递归遍历），空间复杂度：O(N)（哈希表以及树退化成链表时的递归深度）

剑指 Offer 16. 数值的整数次方

难度：中等

最简单的方法是通过循环将 n 个 $x$ 乘起来，时间复杂度为 O(n)。

快速幂法可将时间复杂度降低至 O(log n)。

快速幂的解析（分治法角度和二进制角度）见剑指 Offer 16 题目解析

算法流程：

1. 当 x = 0.0 时：直接返回 0.0，以避免后续 1 除以 0 操作报错。分析：数字 0 的正数次幂恒为 0；0 的 0 次幂和负数次幂没有意义，因此直接返回 0.0 即可。
2. 初始化 res = 1。
3. 当 n < 0 时：把问题转化至 n ≥ 0 的范围内，即执行 x = 1/x，n = - n。
4. 循环计算：当 n = 0 时跳出。
   
   1. 当 n & 1 = 1 时：将当前 x 乘入 res（即 res *= x）。
   2. 执行 x = x²（即 x *= x）。
   3. 执行 n 右移一位（即 n >>= 1）。
5. 返回 res。

class Solution {
    public double myPow(double x, int n) {
        if(x == 0.0f) return 0.0d;
        long b = n;
        double res = 1.0;
        if(b < 0) {
            x = 1 / x;
            b = -b;
        }
        while(b > 0) {
            if((b & 1) == 1) res *= x;
            x *= x;
            b >>= 1;
        }
        return res;
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/57p2pv/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(log N)，空间复杂度：O(1)。

注意，−2147483648 在执行 n = -n 时会越界，所以先将 $n$ 存入 long 变量 b，后面用 b 操作。

另外注意把整除和取余都转化成位运算。

剑指 Offer 33. 二叉搜索树的后序遍历序列

难度：中等

方法一：递归分治

递归解析：

• 终止条件：当 i ≥ j，说明此子树节点数量 ≤ 1，无需判别正确性，因此直接返回 true；
• 递推工作：
  
  1. 划分左右子树：遍历后序遍历的 [i, j] 区间元素，寻找第一个大于根节点的节点，索引记为 m。此时，可划分出左子树区间 [i,m-1] 、右子树区间 [m, j - 1] 、根节点索引 j。
  2. 判断是否为二叉搜索树：
     
     • 左子树区间 [i, m - 1] 内的所有节点都应 < postorder[j]。而第 1.划分左右子树 步骤已经保证左子树区间的正确性，因此只需要判断右子树区间即可。
     • 右子树区间 [m, j - 1] 内的所有节点都应 > postorder[j]。实现方式为遍历，当遇到 ≤ postorder[j] 的节点则跳出；则可通过 p = j 判断是否为二叉搜索树。
• 返回值：所有子树都需正确才可判定正确，因此使用与逻辑符 && 连接。
  
  1. p = j：判断此树是否正确。
  2. recur(i, m - 1)：判断此树的左子树是否正确。
  3. recur(m, j - 1)：判断此树的右子树是否正确。

class Solution {
    public boolean verifyPostorder(int[] postorder) {
        return recur(postorder, 0, postorder.length - 1);
    }
    boolean recur(int[] postorder, int i, int j) {
        if(i >= j) return true;
        int p = i;
        while(postorder[p] < postorder[j]) p++;
        int m = p;
        while(postorder[p] > postorder[j]) p++;
        return p == j && recur(postorder, i, m - 1) && recur(postorder, m, j - 1);
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/5vwbf6/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N²)，空间复杂度：O(N)。（退化成链表）

方法二：辅助单调栈

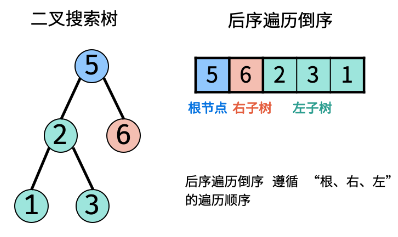
设后序遍历倒序列表为 [r_n, r_n-1, ..., r₁]，遍历此列表，设索引为 i，若为二叉搜索树，则有：

• 当节点值 r_i > r_i+1 时：节点 r_i 一定是节点 r_i+1 的右子节点。

• 当节点值 r_i < r_i+1 时：节点 r_i 一定是某节点 root 的左子节点，且 root 为 r_i+1, r_i+2, ..., r_n 中值大于且最接近 r_i 的节点（∵ root直接连接左子节点 r_i）。

当遍历时遇到递减节点r_i < r_i+1，若为二叉搜索树，则对于后序遍历中节点 r_i 右边的任意节点 r_x ∈ [r_i-1, r_i-2, ..., r₁]，必有节点值 r_x < root。

节点 r_x 只可能为以下两种情况：① r_x 为 r_i 的左、右子树的各节点；② r_x 为 root 的父节点或更高层父节点的左子树的各节点。在二叉搜索树中，以上节点都应小于 root。

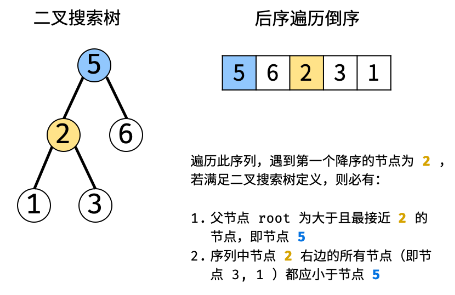
遍历“后序遍历的倒序”会多次遇到递减节点 r_i，若所有的递减节点 r_i 对应的父节点 root 都满足以上条件，则可判定为二叉搜索树。根据以上特点，考虑借助单调栈实现：

1. 借助一个单调栈 stack 存储值递增的节点；
2. 每当遇到值递减的节点 r_i，则通过出栈来更新节点 r_i 的父节点 root；
3. 每轮判断 r_i 和 root 的值关系：
   
   1. 若 r_i > root 则说明不满足二叉搜索树定义，直接返回 false。
   2. 若 r_i < root 则说明满足二叉搜索树定义，则继续遍历。

算法流程：

1. 初始化：单调栈 stack，父节点值 root = +∞（初始值为正无穷大，可把树的根节点看为此无穷大节点的左孩子）；
2. 倒序遍历 postorder：记每个节点为 r_i；
   
   1. 判断：若 r_i > root，说明此后序遍历序列不满足二叉搜索树定义，直接返回 false；
   2. 更新父节点 root： 当栈不为空且 r_i < stack.peek() 时，循环执行出栈，并将出栈节点赋给 root。
   3. 入栈：将当前节点 r_i 入栈；
3. 若遍历完成，则说明后序遍历满足二叉搜索树定义，返回 true。

class Solution {
    public boolean verifyPostorder(int[] postorder) {
        Stack<Integer> stack = new Stack<>();
        int root = Integer.MAX_VALUE;
        for(int i = postorder.length - 1; i >= 0; i--) {
            if(postorder[i] > root) return false;
            while(!stack.isEmpty() && stack.peek() > postorder[i])
                root = stack.pop();
            stack.add(postorder[i]);
        }
        return true;
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/5vwbf6/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(N)。

剑指 Offer 17. 打印从 1 到最大的 n 位数

难度：简单

大数打印解法：

实际上，本题的主要考点是大数越界情况下的打印。需要解决以下三个问题：

1. 表示大数的变量类型：

• 无论是 short / int / long ... 任意变量类型，数字的取值范围都是有限的。因此，大数的表示应用字符串 String 类型。

2. 生成数字的字符串集：

• 使用 int 类型时，每轮可通过 +1 生成下个数字，而此方法无法应用至 String 类型。并且，String 类型的数字的进位操作效率较低，例如 "9999" 至 "10000" 需要从个位到千位循环判断，进位 4 次。
• 观察可知，生成的列表实际上是 n 位 0 - 9 的全排列，因此可避开进位操作，通过递归生成数字的 String 列表。

3. 递归生成全排列：

• 基于分治算法的思想，先固定高位，向低位递归，当个位已被固定时，添加数字的字符串。例如当 n = 2 时（数字范围 1 - 99），固定十位为 0 - 9，按顺序依次开启递归，固定个位 0 - 9，终止递归并添加数字字符串。

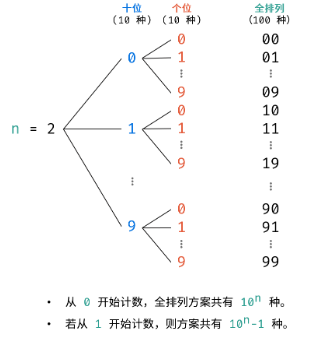
当前的生成方法仍有以下问题：

1. 诸如 00, 01, 02, ⋯ 应显示为 0, 1, 2, ⋯ ，即应删除高位多余的 0;
2. 此方法从 0 开始生成，而题目要求列表从 1 开始；

以上两个问题的解决方法如下：

1. 删除高位多余的 0：

• 字符串左边界定义：声明变量 start 规定字符串的左边界，以保证添加的数字字符串 num[start:] 中无高位多余的 0。例如当 n = 2 时，1 - 9 时 start = 1，10 - 99 时 start = 0。
• 左边界 start 变化规律：观察可知，当输出数字的所有位都是 9 时，则下个数字需要向更高位进 1，此时左边界 start 需要减 1（即高位多余的 0 减少一个）。例如当 n = 3（数字范围 1 - 999）时，左边界 start 需要减 1 的情况有："009" 进位至 "010"，"099" 进位至 "100"。设数字各位中 9 的数量为 nine，所有位都为 9 的判断条件可用以下公式表示：

n − start = nine

• 统计 nine 的方法：固定第 x 位时，当 i = 9 则执行 nine = nine + 1，并在回溯前恢复 nine = nine - 1。

2. 列表从 1 开始：

• 在以上方法的基础上，添加数字字符串前判断其是否为 "0"，若为 "0" 则直接跳过。

本题要求输出 int 类型数组。为运行通过，可在添加数字字符串 $s$ 前，将其转化为 int 类型。

class Solution {
    int[] res;
    int nine = 0, count = 0, start, n;
    char[] num, loop = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
    public int[] printNumbers(int n) {
        this.n = n;
        res = new int[(int)Math.pow(10, n) - 1];
        num = new char[n];
        start = n - 1;
        dfs(0);
        return res;
    }
    void dfs(int x) {
        if(x == n) {
            String s = String.valueOf(num).substring(start);
            if(!s.equals("0")) res[count++] = Integer.parseInt(s);
            if(n - start == nine) start--;
            return;
        }
        for(char i : loop) {
            if(i == '9') nine++;
            num[x] = i;
            dfs(x + 1);
        }
        nine--;
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/5912jv/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(10^N)，空间复杂度：O(10^N)（不算返回值为 O(N)）。

剑指 Offer 51. 数组中的逆序对

难度：困难

「归并排序」与「逆序对」是息息相关的。归并排序体现了“分而治之”的算法思想，具体为：

• 分：不断将数组从中点位置划分开（即二分法），将整个数组的排序问题转化为子数组的排序问题；
• 治：划分到子数组长度为 1 时，开始向上合并，不断将较短排序数组合并为较长排序数组，直至合并至原数组时完成排序；

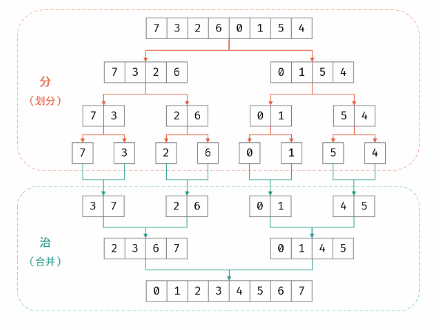
合并阶段本质上是合并两个排序数组的过程，而每当遇到 左子数组当前元素 > 右子数组当前元素 时，意味着「左子数组当前元素 至 末尾元素」与「右子数组当前元素」构成了若干「逆序对」。

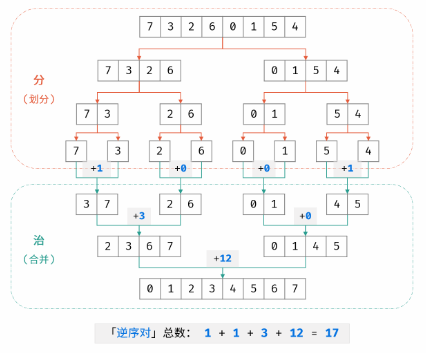
合并期间将两个小排序数组合并为一个大的排序数组，就是找到了这两个小排序数组之间的所有逆序对，以此类推从底至顶合并，就能找到所有逆序对。

因此，考虑在归并排序的合并阶段统计「逆序对」数量，完成归并排序时，也随之完成所有逆序对的统计。

算法流程：
merge_sort() 归并排序与逆序对统计：

1. 终止条件：当 l ≥ r 时，代表子数组长度为 1，此时终止划分；
2. 递归划分：计算数组中点 m，递归划分左子数组 merge_sort(l, m) 和右子数组 merge_sort(m + 1, r)；
3. 合并与逆序对统计：
   
   1. 暂存数组 nums 闭区间 [l, r] 内的元素至辅助数组 tmp；
   2. 循环合并：设置双指针 i, j 分别指向左 / 右子数组的首元素；
      
      • 当 i = m + 1 时：代表左子数组已合并完，因此添加右子数组当前元素 tmp[j]，并执行 j = j + 1；
      • 否则，当 j = r + 1 时：代表右子数组已合并完，因此添加左子数组当前元素 tmp[i]，并执行 i = i + 1；
      • 否则，当 tmp[i] ≤ tmp[j] 时：添加左子数组当前元素 tmp[i]，并执行 i = i + 1；
      • 否则（即 tmp[i] > tmp[j]）时：添加右子数组当前元素 tmp[j]，并执行 j = j + 1；此时构成 m - i + 1 个「逆序对」，统计添加至 res；
4. 返回值：返回直至目前的逆序对总数 res；

reversePairs() 主函数：

1. 初始化：辅助数组 tmp，用于合并阶段暂存元素；
2. 返回值：执行归并排序 merge_sort()，并返回逆序对总数即可；

class Solution {
    int[] nums, tmp;
    public int reversePairs(int[] nums) {
        this.nums = nums;
        tmp = new int[nums.length];
        return mergeSort(0, nums.length - 1);
    }
    private int mergeSort(int l, int r) {
        // 终止条件
        if (l >= r) return 0;
        // 递归划分
        int m = (l + r) / 2;
        int res = mergeSort(l, m) + mergeSort(m + 1, r);
        // 合并阶段
        int i = l, j = m + 1;
        for (int k = l; k <= r; k++)
            tmp[k] = nums[k];
        for (int k = l; k <= r; k++) {
            if (i == m + 1)
                nums[k] = tmp[j++];
            else if (j == r + 1 || tmp[i] <= tmp[j])
                nums[k] = tmp[i++];
            else {
                nums[k] = tmp[j++];
                res += m - i + 1; // 统计逆序对
            }
        }
        return res;
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/o53yjd/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(NlogN)，空间复杂度：O(N)。