剑指offer一刷：栈与队列

剑指 Offer 09. 用两个栈实现队列

难度：简单

设计栈 A 用于加入队尾操作，栈 B 用于将元素倒序，从而实现删除队首元素。

class CQueue {
    LinkedList<Integer> A, B;
    public CQueue() {
        A = new LinkedList<Integer>();
        B = new LinkedList<Integer>();
    }
    public void appendTail(int value) {
        A.addLast(value);
    }
    public int deleteHead() {
        if(!B.isEmpty()) return B.removeLast();
        if(A.isEmpty()) return -1;
        while(!A.isEmpty())
            B.addLast(A.removeLast());
        return B.removeLast();
    }
}

作者：Krahets
链接：https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/5dq0t5/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

注意，Stack 继承了 Vector 接口，而 Vector 底层是一个 Object[] 数组，那么就要考虑空间扩容和移位的问题了，并且是线程安全的，性能很低。 可以使用 LinkedList 来做 Stack 的容器，因为 LinkedList 实现了 Deque 接口，所以 Stack 能做的事 LinkedList 都能做，其本身结构是个双向链表，扩容消耗少。

此外，评论里说，官方建议的创建栈的方式是这样的：

Deque<Integer> stack = new ArrayDeque<>();

时间复杂度：O(1)，空间复杂度：O(N)。

剑指 Offer 30. 包含 min 函数的栈

难度：简单

借助辅助栈（非严格降序）实现：

class MinStack {
    Stack<Integer> A, B;
    public MinStack() {
        A = new Stack<>();
        B = new Stack<>();
    }
    public void push(int x) {
        A.add(x);
        if(B.empty() || B.peek() >= x)
            B.add(x);
    }
    public void pop() {
        if(A.pop().equals(B.peek()))
            B.pop();
    }
    public int top() {
        return A.peek();
    }
    public int min() {
        return B.peek();
    }
}

作者：Krahets
链接：https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/50je8m/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

这里为了便于理解，还是使用的 Stack。实际中建议使用 LinkedList。

时间复杂度：O(1)，空间复杂度：O(N)。

剑指 Offer 59 - I. 滑动窗口的最大值

难度：困难

暴力法的时间复杂度为 $\approx O(nk)$。

本题难点：如何在每次窗口滑动后，将“获取窗口内最大值”的时间复杂度从 O(k) 降低至 O(1)。

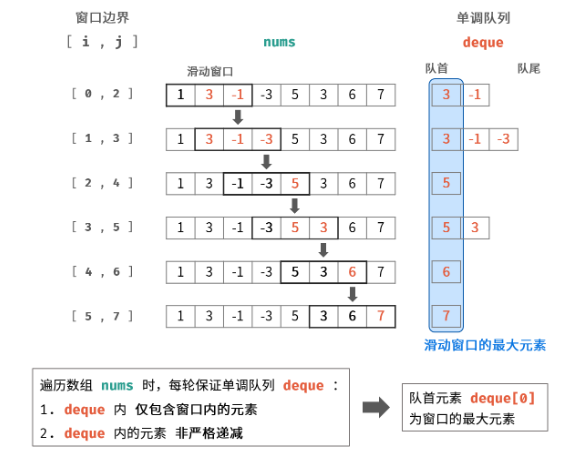
考虑采用单调队列解决以上问题。

遍历数组时，每轮保证单调队列 deque：

1. deque 内仅包含窗口内的元素 ⇒ 每轮窗口滑动移除了元素 nums[i - 1]，需将 deque 内的对应元素一起删除。
2. deque 内的元素非严格递减 ⇒ 每轮窗口滑动添加了元素 nums[j + 1]，需将 deque 内所有 < nums[j + 1] 的元素删除。

本算法基于问题的一个重要性质：当一个元素进入队列的时候，它前面所有比它小的元素就不会再对答案产生影响。

举个例子，如果我们向队列中插入数字序列 1 1 1 1 2，那么在第一个数字 2 被插入后，数字 2 前面的所有数字 1 将不会对结果产生影响。因为按照队列的取出顺序，数字 2 只能在所有的数字 1 被取出之后才能被取出，因此如果数字 1 如果在队列中，那么数字 2 必然也在队列中，使得数字 1 对结果没有影响。

算法流程：

1. 初始化：双端队列 deque，结果列表 res，数组长度 n；
2. 滑动窗口：左边界范围 i ∈ [1 − k, n − k]，右边界范围 j ∈ [0, n − 1]；
   
   1. 若 i > 0 且 队首元素 deque[0] = 被删除元素 nums[i - 1]：则队首元素出队；
   2. 删除 deque 内所有 < nums[j] 的元素，以保持 deque 递减；
   3. 将 nums[j] 添加至 deque 尾部；
   4. 若已形成窗口（即 i ≥ 0 ）：将窗口最大值（即队首元素 deque[0]）添加至列表 res；
3. 返回值：返回结果列表 res；

可以将“未形成窗口”和“形成窗口后”两个阶段拆分到两个循环里实现。代码虽变长，但减少了冗余的判断操作。

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if(nums.length == 0 || k == 0) return new int[0];
        Deque<Integer> deque = new LinkedList<>();
        int[] res = new int[nums.length - k + 1];
        // 未形成窗口
        for(int i = 0; i < k; i++) {
            while(!deque.isEmpty() && deque.peekLast() < nums[i])
                deque.removeLast();
            deque.addLast(nums[i]);
        }
        res[0] = deque.peekFirst();
        // 形成窗口后
        for(int i = k; i < nums.length; i++) {
            if(deque.peekFirst() == nums[i - k])
                deque.removeFirst();
            while(!deque.isEmpty() && deque.peekLast() < nums[i])
                deque.removeLast();
            deque.addLast(nums[i]);
            res[i - k + 1] = deque.peekFirst();
        }
        return res;
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/58rgqe/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(k)。

剑指 Offer 59 - II. 队列的最大值

难度：中等

如下图所示，最直观的想法是维护一个最大值变量，在元素入队时更新此变量即可；但当最大值出队后，并无法确定下一个次最大值，因此不可行。

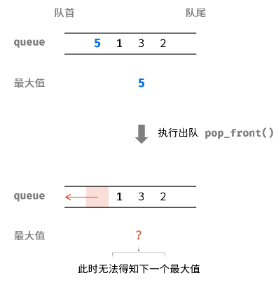
同上题，采用递减的单调队列（双向队列）来实现

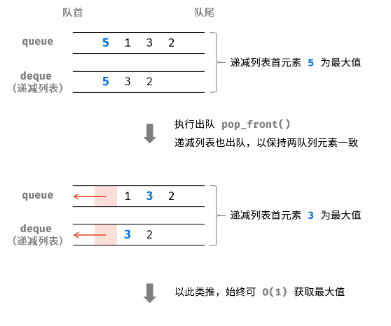
函数设计：

初始化队列 queue，双向队列 deque；

最大值 max_value()：

• 当双向队列 deque 为空，则返回 -1；
• 否则，返回 deque 首元素；

入队 push_back()：

1. 将元素 value 入队 queue；
2. 将双向队列中队尾所有小于 value 的元素弹出（以保持 deque 非严格递减），并将元素 value 入队 deque；

出队 pop_front()：

1. 若队列 queue 为空，则直接返回 -1；
2. 否则，将 queue 首元素出队；
3. 若 deque 首元素和 queue 首元素相等，则将 deque 首元素出队（以保持两队列元素一致）；

注：设计双向队列为非严格递减的原因：若队列 queue 中存在两个值相同的最大元素，此时 queue 和 deque 同时弹出一个最大元素，而 queue 中还有一个此最大元素；即采用严格单调递减将导致两队列中的元素不一致。

class MaxQueue {
    Queue<Integer> queue;
    Deque<Integer> deque;
    public MaxQueue() {
        queue = new LinkedList<>();
        deque = new LinkedList<>();
    }
    public int max_value() {
        return deque.isEmpty() ? -1 : deque.peekFirst();
    }
    public void push_back(int value) {
        queue.offer(value);
        while(!deque.isEmpty() && deque.peekLast() < value)
            deque.pollLast();
        deque.offerLast(value);
    }
    public int pop_front() {
        if(queue.isEmpty()) return -1;
        if(queue.peek().equals(deque.peekFirst()))
            deque.pollFirst();
        return queue.poll();
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/e2tfiv/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(1)，空间复杂度：O(N)。

注：三种方法的均摊时间复杂度均为 O(1)，max_value 和 pop_front 方法很好理解，对于 push_back 方法，例如 543216，只有最后一次 push_back 操作是 O(n)，其他每次操作的时间复杂度都是 O(1)，均摊时间复杂度为 (O(1)×(n−1)+O(n))/n=O(1)。（本质上 n 个元素入出队列总共为 O(n)，均摊下来确实为 O(1)）。