2025杭电多校第九场 乘法逆元、阿斯蒂芬、计算几何 个人题解
计算几何
计算几何
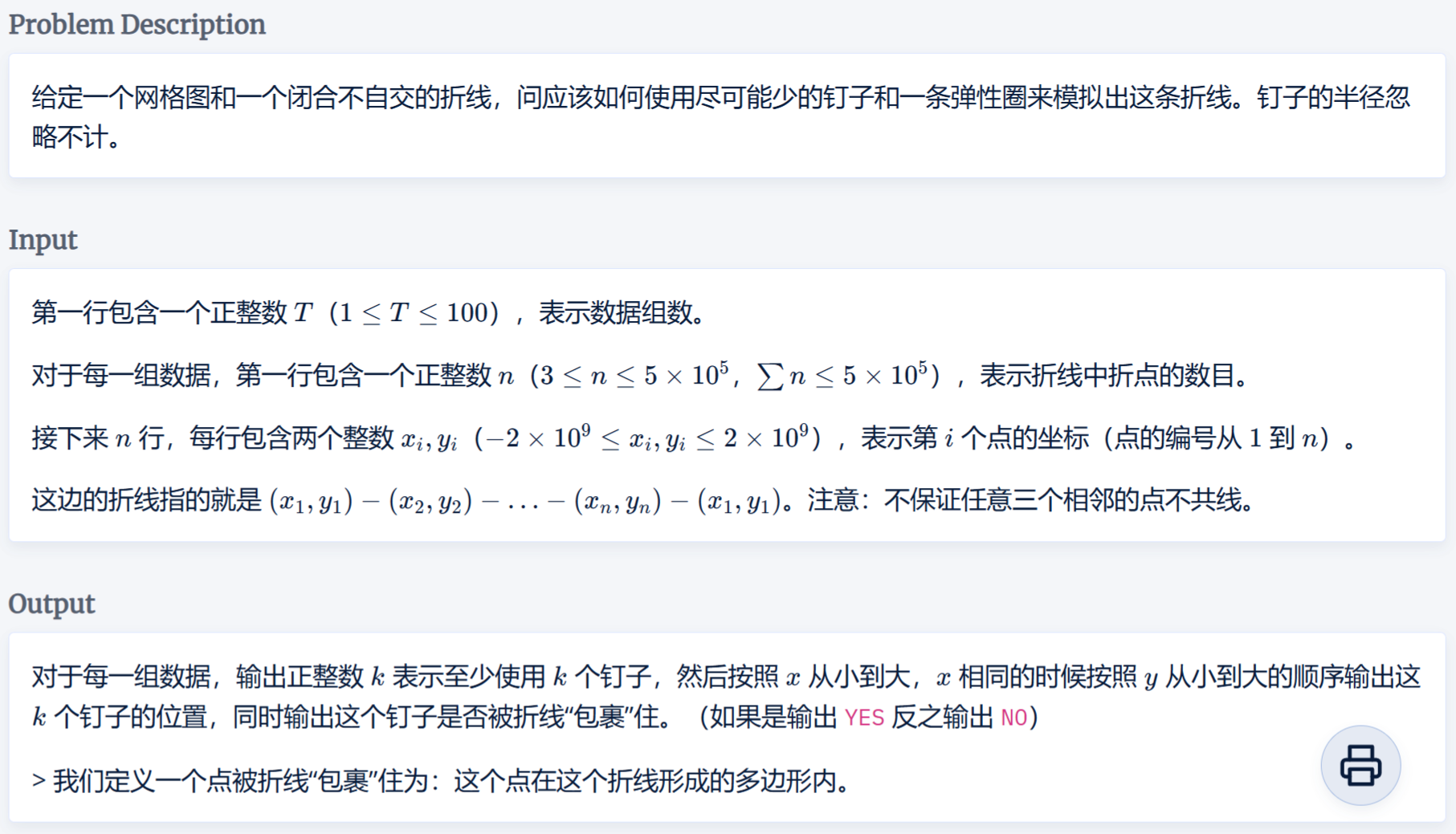
题目
思路
由于给定的是一条不自交的折线，因此可以直接沿着给定的折线来走
如果下一个点相对于当前的前进方向是向左，那么当前点标记为1，否则为0
判断方向可以通过相邻的两个线段的向量的叉乘正负性
最后根据给定的折线是顺时针还是逆时针来判断1、0对应的是\(YES,NO\)
如何判断给定的折线是顺时针还是逆时针呢？
可以对相邻的两个点的向量进行叉乘后累加，计算这个多边形的面积，最后判断总面积的正负形就可以知道给定的折线是顺时针还是逆时针了
特别需要注意的是，由于给定的点都是整数，叉乘计算出来的数也是整数，如果用板子里自带的\(double\)类型的变量和函数，将会出现精度问题！！
赛时因为这个问题\(WA\)了8发
代码实现
#include<iostream>
#include<vector>
#include<cmath>
#include<queue>
#include<algorithm>
#include<unordered_map>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(int i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
constexpr int inf = 1e9 ;
#define double ll
#define int ll
const double eps=1e-6;
const int N=5e5+5;
const double pi=acos(1.0*-1);
struct Vector {
double x, y;
Vector():x(0),y(0){}
Vector(double a, double b) :x(a), y(b) {}
bool operator<(const Vector&t)const{
if(x!=t.x)return x<t.x;
return y<t.y;
}
};
struct node{
Vector v;
int pd;
bool operator<(const node&t)const{
return v<t.v;
}
}a[N];
Vector operator+(Vector a, Vector b) {
return Vector(a.x + b.x, a.y + b.y);
}
Vector operator-(Vector a, Vector b) {
return Vector(a.x - b.x, a.y - b.y);
}
double operator*(Vector a, Vector b) {
return a.x * b.y - a.y * b.x;
}
double cross(Vector a, Vector b, Vector c) {
return (b - a) * (c - a);
}
double operator&(Vector a, Vector b) {
return a.x * b.x + a.y * b.y;
}
double dot(Vector a, Vector b, Vector c) {
return (b - a) & (c - a);
}
void eachT() {
int n;cin>>n;
int cnt=0;
rep(i,1,n){
cin>>a[i].v.x>>a[i].v.y;
}
Vector v=a[n].v-a[n-1].v;
Vector last=a[n].v;
int S=0;
rep(i,1,n){
Vector p,now;
S+=a[i].v*a[(i-1-1+n)%n+1].v;
p=a[i].v;
now=p-last;
if((v*now)==0){
a[(i-1-1+n)%n+1].pd=0;
last=p;
v=now;
continue;
}else if(v*now>0){
a[(i-1-1+n)%n+1].pd=1;
}else{
a[(i-1-1+n)%n+1].pd=-1;
}
cnt++;
last=p;
v=now;
}
sort(a+1,a+1+n);
cout<<cnt<<'\n';
if(S<0){
rep(i,1,n){
if(a[i].pd!=0){
cout<<a[i].v.x<<" "<<a[i].v.y<<" ";
if(a[i].pd==1)cout<<"YES\n";
else cout<<"NO\n";
}
}
}else{
rep(i,1,n){
if(a[i].pd!=0){
cout<<a[i].v.x<<" "<<a[i].v.y<<" ";
if(a[i].pd==-1)cout<<"YES\n";
else cout<<"NO\n";
}
}
}
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
ll t = 1;
cin >> t;
while (t--) {
eachT();
}
}
阿斯蒂芬
强联通分量 #dfs
题目
思路
易知，对于一个强联通分量，其中的点都可以互相抵达，那么能量就可以在这个块中无限增长
而题目中有一个特别容易出错的细节，沉寂操作只能不让该节点的能量累积到\(T\)中，实际上能量还是在块中无限增长的
也就是说，如果当前连通块内有能量，那么连通块能够到达的点也都会能量无限增长，这些点也都必须要沉寂！
首先很明显需要\(tarjan\)缩点，缩点时需要将点的权值以及点的大小记录下来，缩点后的新图是一个有向无环图
为了沉寂连通块也能到达的点，建新图的时候需要反向建边，相当于从能量源头出发dfs
接下来在新图上进行dfs：
数组\(vis[N]\)有三个状态：
- \(vis[u]=1\)代表返回节点\(u\)的路上包含缩过的点，并且含有能量
- \(vis[u]=2\)代表返回节点\(u\)的路上都是没缩过的点，并且含有能量
- \(vis[u]=3\)代表返回节点\(u\)的路上没有能量
通过这样三种状态，我们可以一边dfs一边染色一边更新答案
对于\(vis[u]=1\)的点，这个点是必须要沉寂的，可以直接算入答案中
伪代码： - 入点：
- \(bool\)型变量\(val\)代表当前点\(u\)是否有能量，初始为\(0\)
- 遍历所有子节点\(son\)：
- 如果\(vis[son]=3\)，儿子节点无能量，\(continue\)
- 如果\(vis[son]=2\)，儿子节点有能量，更新\(val\)，\(continue\)
- 如果\(vis[son]=1\)，儿子节点有能量并且路上包含缩过的点，\(vis[u]=1\)，\(break\)
- \(val\ |\ =dfs(son,u)\)，递归dfs
- 回溯：如果\(vis[son]=1\)，儿子节点有能量并且路上包含缩过的点，\(vis[u]=1\)，\(break\)
- 离点：
- 如果\(u\)本身就有能量，更新\(val\)
- 如果\(vis[u]\)还没被更新过：
- 如果\(val=0\)，\(vis[u]=3\)，不包含能量
- 否则如果\(size[u]>1\)，\(vis[u]=1\)，包含缩过的点且有能量
- 否则\(vis[u]=2\)，不包含缩过的点但有能量
- 如果\(vis[u]=1\)，更新答案，加入\(size[u]\)个需要沉寂的点
- 返回\(val\)
代码实现
#include<iostream>
#include<vector>
#include<cmath>
#include<queue>
#include<algorithm>
#include<set>
#include<stack>
#include<unordered_map>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(int i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
const int N = 5e5 + 5;
int n, w[N], b[N];
struct node {
vector<int>e;
int dfn, low, in, scc;
}a[N];
struct node1 {
set<int>e;
int siz, w;
}na[N];
stack<int>st;
int tot, cnt;
void tarjan(int u) {
a[u].dfn = a[u].low = ++tot;
st.push(u), a[u].in = 1;
for (auto& son : a[u].e) {
if (!a[son].dfn) {
tarjan(son);
a[u].low = min(a[u].low, a[son].low);
} else if (a[son].in) {
a[u].low = min(a[u].low, a[son].low);
}
}
if (a[u].dfn == a[u].low) {
int v;++cnt;
do {
v = st.top(), st.pop(), a[v].in = 0;
a[v].scc = cnt, ++na[cnt].siz;
na[cnt].w += w[v];
} while (u != v);
}
}
void build(int n) {
rep(i, 1, n) {
for (auto& son : a[i].e) {
if (a[i].scc != a[son].scc) {
na[a[son].scc].e.insert(a[i].scc);
}
}
}
}
unordered_map<int, int>vis;
int ans;
bool dfs(int u, int fa) {
bool val = 0;
for (auto& son : na[u].e) {
if (son == fa || vis[son] == 3)continue;//3 无能量
if (vis[son] == 2) { val |= 1;continue; }//2 无环有能量
if (vis[son] == 1) { vis[u] = 1;break; }//1 有环有能量
val |= dfs(son, u);
if (vis[son] == 1) { vis[u] = 1; }
}
val |= (na[u].w > 0);
if (vis[u] != 1) {
if (!val)vis[u] = 3;
else if (na[u].siz > 1)vis[u] = 1;
else vis[u] = 2;
}
if (vis[u] == 1)ans += na[u].siz;
return val;
}
void init() {
vis.clear();
ans = tot = cnt = 0;
while (st.size())st.pop();
rep(i, 1, n) {
a[i].e.clear();
a[i].dfn = a[i].in = a[i].low = a[i].scc = 0;
na[i].e.clear();
na[i].siz = na[i].w = 0;
}
}
void eachT() {
cin >> n;
init();
rep(i, 1, n)cin >> w[i];
rep(i, 1, n)cin >> b[i];
rep(i, 1, n) {
rep(j, 1, b[i]) {
int x;cin >> x;
a[i].e.push_back(x);
}
}
rep(i, 1, n) {
if (!a[i].scc)tarjan(i);
}
build(n);
rep(i, 1, cnt) {
if (vis[i] == 0)dfs(i, 0);
}
cout << ans << '\n';
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
ll t = 1;
cin >> t;
while (t--) {
eachT();
}
}
乘法逆元
数学 #位运算
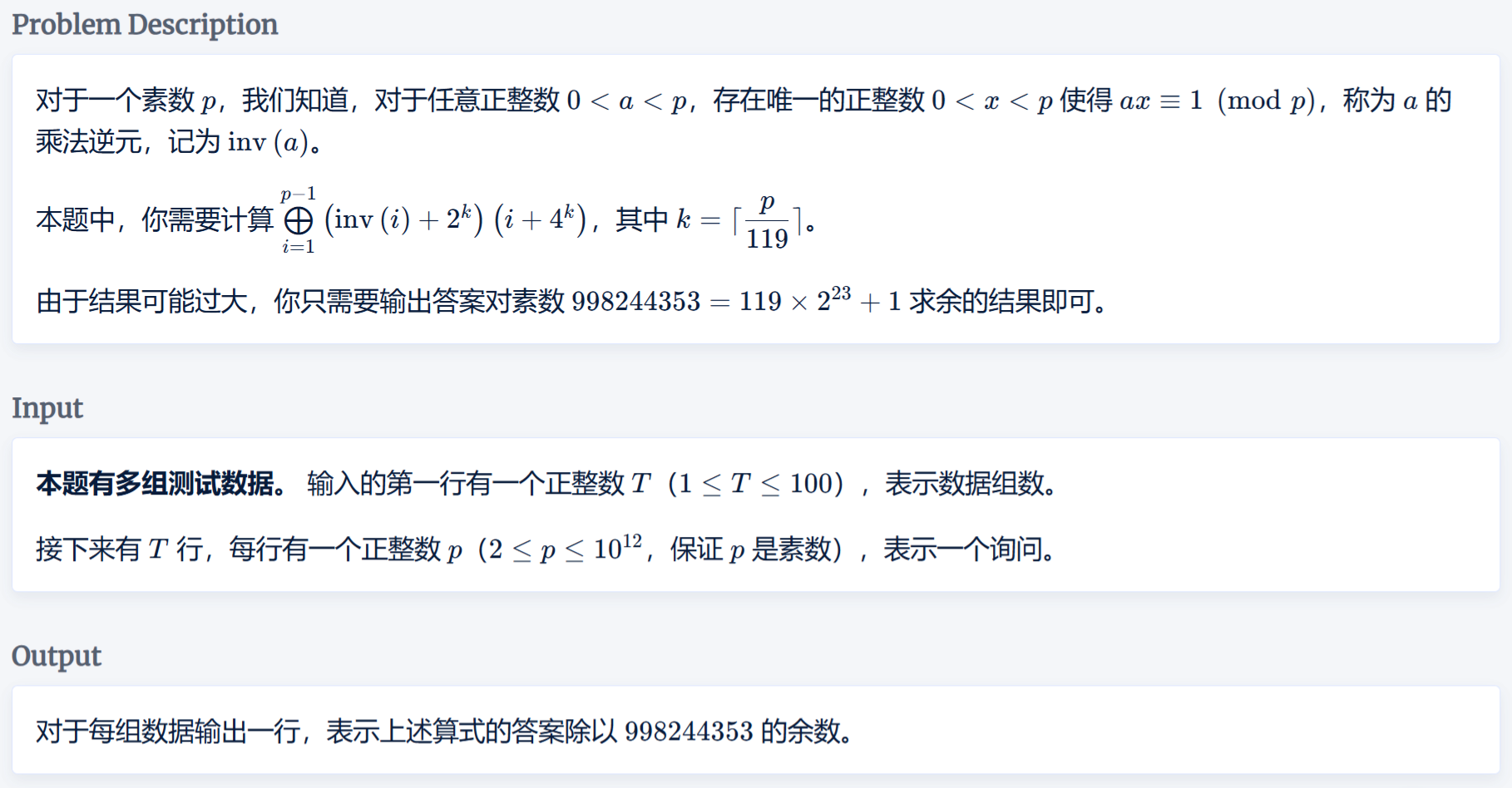
题目
思路
\[\begin{align}
&\bigoplus_{i=1}^{p-1}(inv(i)+2^k)(i+4^k)\mod{M}\\ \\
&=\bigoplus_{i=1}^{p-1}i\times inv(i)+i\times2^k+inv(i)\times 2^{2k}+2^{3k} \mod{M}
\end{align}
\]
当\(k\geq 23\)时，\(p\leq 23\times 119<2^{23}\leq 2^k\)
则有\(i<p<2^k,inv(i)<p<2^k\)
则有：
\[\begin{align}
\begin{array}{lc}
&i\times inv(i)&<i\times2^k&<2^k\times 2^k&<inv(i)\times2^k&<2^{3k} \\ \\
&0\sim 2^k &2^{k}\sim 2^{2\times k}& &2^{2\times k}\sim2^{3\times k}&2^{3\times k}
\end{array}
\end{align}
\]
发现四个项的值所在的区间完全错开，这就意味着他们的二进制表示的位数范围是完全错开的，意味着他们的二进制运算是互不干扰的
因此原式可以转化为：
\[\bigoplus_{i=1}^{p-1}i\times inv(i)+\bigoplus_{i=1}^{p-1}i\times2^k+\bigoplus_{i=1}^{p-1}inv(i)\times 2^{2k}+\bigoplus_{i=1}^{p-1}2^{3k}\mod{M}
\]
由于\(i\leq p,inv(i)\leq p\)且\(i\)与\(inv(i)\)一一对应，所以\(inv(i)\)为\(1\sim p-1\)的排列
则有\(\bigoplus_{i=1}^{p-1}i=\bigoplus_{i=1}^{p-1}inv(i)\)
对于\(\bigoplus_{i=1}^{p-1}i\times inv(i)\)：
- 由于\(i\times inv(i)\equiv 1\mod{p}\)，则\(inv(1)=1,inv(p-1)=p-1\)
- 对于\([a\times inv(a)]\oplus[b\times inv(b)]\)，若\(b=inv(a)\)，则\(a\times inv(a)=inv(b)\times inv(inv(b))=inv(b)\times b\)，则\([a\times inv(a)]\oplus[b\times inv(b)]=0\)
- 在\(1\sim p\)中，除了\(1,p-1\)以外，剩下的都可以\(a=inv(b)\)一一配对消去
- 因此\(\bigoplus_{i=1}^{p-1}i\times inv(i)=1\oplus(p-1)^2\)
- 为素数，\(p-1\)则必为偶数，\((p-1)^2\)必为偶数，与1异或后不变
- 因此\(\bigoplus_{i=1}^{p-1}i\times inv(i)=(p-1)^2\)
对于\(\bigoplus_{i=1}^{p-1}i\times2^k\)：
- 由于与2的幂次做乘法就相当于右移，所以\(\bigoplus_{i=1}^{p-1}i\times2^k=2^k\times\bigoplus_{i=1}^{p-1}i\)
- 对于\(\oplus_{i=1}^{p-1}i\)，发现\(i\oplus i+1\oplus i+2\oplus i+3=0\)，记\(c=(p-1)\%4\)，则原式等于序列最后\(c\)项的异或和
- 将最后\(c\)项的异或和记为\(S\)，则\(\bigoplus_{i=1}^{p-1}i\times2^k=2^k\times S\)
对于\(\bigoplus_{i=1}^{p-1}inv(i)\times 2^{2k}\)：
- 同理等于\(2^{2k}\times \oplus_{i=1}^{p-1}inv(i)\)
- 由\(\bigoplus_{i=1}^{p-1}i=\bigoplus_{i=1}^{p-1}inv(i)\)，原式等于\(2^{2k}\times \oplus_{i=1}^{p-1}i=2^{2k}\times S\)
对于\(\bigoplus_{i=1}^{p-1}2^{3k}\)：
- \(p\)为素数，则\(p-1\)必为偶数，\(\bigoplus_{i=1}^{p-1}2^{3k}=2^{3k}\times\oplus_{i=1}^{p-1}1=0\)
则题干要求的原式可以化为：
\[(p-1)^2+(2^k+2^{2k})\times S\mod{M}
\]
计算时要注意减法取模前要加模数\(M\)
当\(k<23\)时，暴力计算即可
但是需要注意，异或运算不可以一边取模一边算，所以再算完异或和之后再取模
代码实现
#include<iostream>
#include<vector>
#include<map>
#include<cmath>
#include<set>
#include<stack>
#include<unordered_map>
using namespace std;
using ll = long long;
using ull =unsigned long long;
#define int ull
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(int i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
constexpr int inf = 1e9 + 5;
constexpr int mod=998244353;
int p;
int qpow(int a,int b,int m){
int ans=1;a%=m;
while(b){
if(b%2){ans*=a;ans%=m;}
a*=a;a%=m;b>>=1;
}
return ans%m;
}
void eachT() {
cin>>p;
int k=(p+118)/119;
if(k<=22){
int ans=0;
rep(i,1,p-1){
ans^= (qpow(i,p-2,p)+(1ull<<k))*(i+(1ull<<2*k));
}
cout<<ans%mod<<'\n';
}else{
int cnt=(p-1)%4,s=0;
rep(i,0,cnt)s^=p-1-i;
s%=mod;
int pw2=qpow(2,k,mod);
int part1=(pw2*pw2+pw2)%mod*s%mod;
p%=mod;
int part2=(p*p%mod-2*p%mod+2+mod)%mod;
cout<<(part1+part2)%mod<<'\n';
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
ll t = 1;
cin >> t;
while (t--) {
eachT();
}
}
浙公网安备 33010602011771号