GLV HDU6482 HDU5852

GLV的maxn开两倍，防止溢出。

HDU6482

题意：给你x1,x2,y1,y2  (x1<x2,y1<y2)，问你从(0,y1)->(x1,0),(0,y2)->(0,x2),只能往右、往下走的时候的路径不相交的条数是多少。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=(int)1e9+7;
const int maxn=200005;
ll fac[maxn+5],inv_fac[maxn+5];

ll quick(ll a,ll b){
    ll ans=1;
    while(b){
        if(b&1) ans=ans*a%mod;
        a=a*a%mod;
        b/=2;
    }
    return ans;
}
void init(){
    inv_fac[0]=fac[0]=1,fac[1]=inv_fac[1]=1;
    for(int i=2;i<maxn;i++)
        fac[i]=fac[i-1]*i%mod;
    inv_fac[maxn-1]=quick(fac[maxn-1],mod-2);
    for(int i=maxn-2;i>=0;i--)
        inv_fac[i]=inv_fac[i+1]*(i+1)%mod;
}

ll C(ll n,ll m){
    if(n<0||m<0||m>n) return 0;
    if(n==m||m==0) return 1;
    return fac[n]*inv_fac[n-m]%mod*inv_fac[m]%mod;
}
ll x[2],y[2];
int main(){
    init();
    int t;
    cin>>t;
    while(t--){
        scanf("%lld%lld%lld%lld",&x[0],&x[1],&y[0],&y[1]);
        ll ans1=C(x[1]+y[1],y[1]),ans2=C(x[0]+y[1],y[1]);
        ll ans3=C(y[0]+x[1],y[0]),ans4=C(x[0]+y[0],y[0]);
        printf("%lld\n",((ans1*ans4-ans2*ans3)%mod+mod)%mod);

    }
   return 0;
}

HDU5852

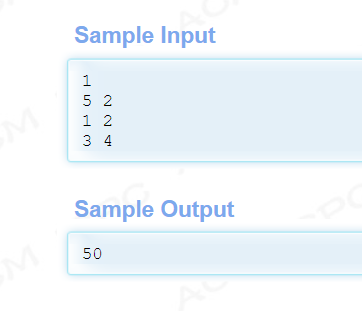
题意:给你一个n*n的矩阵，再第一行一次有k个起点1<=a1<a2<a3<...<ak<=n；最后一行有n个终点1<=b1<b2<b3<...<bk<=n；你只能向右或向下走，问你有多少种路线方案，使得ai->bi  i=1...n；答案mod 1e9+7

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long int ll;

const int MAXN = 2e5 + 10;
ll jc[MAXN];
ll inv[MAXN];



const ll MOD = 1e9 + 7;
const int N = 1e2 + 10;
ll a[N][N];

ll pow(ll a, ll n, ll p)    //快速幂 a^n % p
{
    ll ans = 1;
    while (n) {
        if (n & 1) ans = ans * a % p;
        a = a * a % p;
        n >>= 1;
    }
    return ans;
}

ll niYuan(ll a, ll b)   //费马小定理求逆元
{
    return pow(a, b - 2, MOD);
}


inline ll C(int a, int b)    //计算C(a, b),a下，b上
{
    if (b > a) return 0;
    return jc[a] * inv[b] % MOD
        * inv[a - b] % MOD;
}

void init()
{
    ll p = 1;
    jc[0] = 1;
    jc[1] = 1;
    inv[0] = 1;
    inv[1] = 1;
    for (int i = 2;i < MAXN;i++) {
        p = (p * i) % MOD;
        jc[i] = p;
        //inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;
    }

    for (int i = 2;i < MAXN;i++) inv[i] = inv[MOD % i] * (MOD - MOD / i) % MOD;   //O(n)求逆元
    for (int i = 2;i < MAXN;i++) inv[i] = inv[i - 1] * inv[i] % MOD;   //扩展到i!的逆元
}


ll determinant(int n)
{
    //a为方阵
    //MOD根据实际情况而定
    ll ans = 1;
    for (int k = 1;k <= n;k++)  //将a[k+1..n][k]都变成0
    {
        ll pos = -1;
        for (int i = k;i <= n;i++)  //找到a[k..n][k]中第一个非0元素
            if (a[i][k])
            {
                pos = i;
                break;
            }
        if (pos == -1)return 0;  //没有的话行列式值为0
        if (pos != k)  //将找到的那一行换到第k行，swap(a[k],a[pos])
            for (int j = k;j <= n;j++)swap(a[pos][j], a[k][j]);
        ll inv = niYuan(a[k][k], MOD);
        for (int i = k + 1;i <= n;i++)
            if (a[i][k])
            {
                ans = ans * inv % MOD;   //下面的计算中第i行提高a[k][k]倍，所以答案需要除以a[k][k]才是正解
                for (int j = k + 1;j <= n;j++)
                    a[i][j] = ((a[i][j] * a[k][k] % MOD - a[k][j] * a[i][k] % MOD) % MOD + MOD) % MOD;
                a[i][k] = 0;
            }
    }
    for (int i = 1;i <= n;i++)
        ans = ans * a[i][i] % MOD;
    return ans;
}

int A[N], B[N];


int main()
{
    int t;
    init();
    scanf("%d", &t);
    while (t--)
    {
        int n, k;
        scanf("%d%d", &n, &k);
        for (int i = 1;i <= k;i++) scanf("%d", &A[i]);
        for (int i = 1;i <= k;i++) scanf("%d", &B[i]);

        for (int i = 1;i <= k;i++)
        {
            for (int j = 1;j <= k;j++)
            {
                a[i][j] = C(n + B[j] - (1 + A[i]), n - 1);
            }
        }
        printf("%lld\n", determinant(k));
    }
}