【BZOJ4816】[Sdoi2017]数字表格 莫比乌斯反演

【BZOJ4816】[Sdoi2017]数字表格

Description

Doris刚刚学习了fibonacci数列。用f[i]表示数列的第i项，那么

f[0]=0

f[1]=1

f[n]=f[n-1]+f[n-2],n>=2

Doris用老师的超级计算机生成了一个n×m的表格，第i行第j列的格子中的数是f[gcd(i,j)]，其中gcd(i,j)表示i,j的最大公约数。Doris的表格中共有n×m个数，她想知道这些数的乘积是多少。答案对10^9+7取模。

Input

有多组测试数据。

第一个一个数T，表示数据组数。

接下来T行，每行两个数n,m

T<=1000,1<=n,m<=10^6

Output

输出T行，第i行的数是第i组数据的结果

Sample Input

3
2 3
4 5
6 7

Sample Output

1
6
960

题解：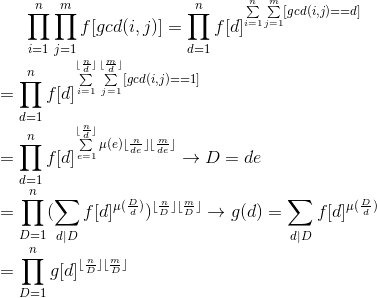

然后O(nlogn)预处理g(i)即可。

P.S.：最后一行打错了，d应该是D。

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
const int maxn=1000010;
int N=1000000,num;
ll ans;
ll f[maxn],f1[maxn],g[maxn],sg[maxn],sg1[maxn];
int mu[maxn],pri[maxn/10];
bool np[maxn];
ll pm(ll x,ll y)
{
	ll z=1;
	while(y)
	{
		if(y&1)	z=z*x%mod;
		x=x*x%mod,y>>=1;
	}
	return z;
}
void init()
{
	int i,j;
	mu[1]=1;
	f[0]=0,f[1]=f1[1]=1;
	for(i=2;i<=N;i++)
	{
		f[i]=(f[i-2]+f[i-1])%mod,f1[i]=pm(f[i],mod-2);
		if(!np[i])	pri[++num]=i,mu[i]=-1;
		for(j=1;j<=num&&i*pri[j]<=N;j++)
		{
			np[i*pri[j]]=1;
			if(i%pri[j]==0)	break;
			mu[i*pri[j]]=-mu[i];
		}
	}
	for(i=1;i<=N;i++)	g[i]=1;
	for(i=1;i<=N;i++)
	{
		for(j=1;i*j<=N;j++)
		{
			if(mu[j]==1)	g[i*j]=g[i*j]*f[i]%mod;
			if(mu[j]==-1)	g[i*j]=g[i*j]*f1[i]%mod;
		}
	}
	sg[0]=sg1[0]=1;
	for(i=1;i<=N;i++)	sg[i]=sg[i-1]*g[i]%mod,sg1[i]=pm(sg[i],mod-2);
}
void work()
{
	int n,m,i,last;
	scanf("%d%d",&n,&m);
	if(n>m)	swap(n,m);
	ans=1;
	for(i=1;i<=n;i=last+1)
	{
		last=min(n/(n/i),m/(m/i));
		ans=ans*pm(sg[last]*sg1[i-1]%mod,(ll)(n/i)*(m/i))%mod;
	}
	printf("%lld\n",ans);
}
int main()
{
	init();
	int T;
	scanf("%d",&T);
	while(T--)	work();
	return 0;
}