树状数组学习笔记

未完待续 ...

目录

• 1. 树状数组原理
  • 1. 引入
  • 2. 树状数组
• 2. 树状数组普通应用
  • 1. 单点修改单点查询
  • 2. 单点加区间求和
  • 3. 区间加单点查询
  • 4. 区间加区间求和
  • 5. 树状数组求逆序对
• 3. 优化
  • 1. \(O(n)\) 建树
  • 2. 时间戳优化
  • 3. 查询优化
  • 4. k 叉树状数组
    • 1. 整数叉树状数组
    • 2. \(\phi\) 叉树状数组
    • 3. 总结
• 4. 树状数组中级应用
  • 1. 单点加区间最值
  • 2. 静态区间最值
  • 3. 二维树状数组
• 5. 树状数组高级应用
  • 1. 树状数组加 lazytag
  • 2. 可持久化树状数组
  • 3. 树状数组实现 BST 的功能
• Reference

1. 树状数组原理

1. 引入

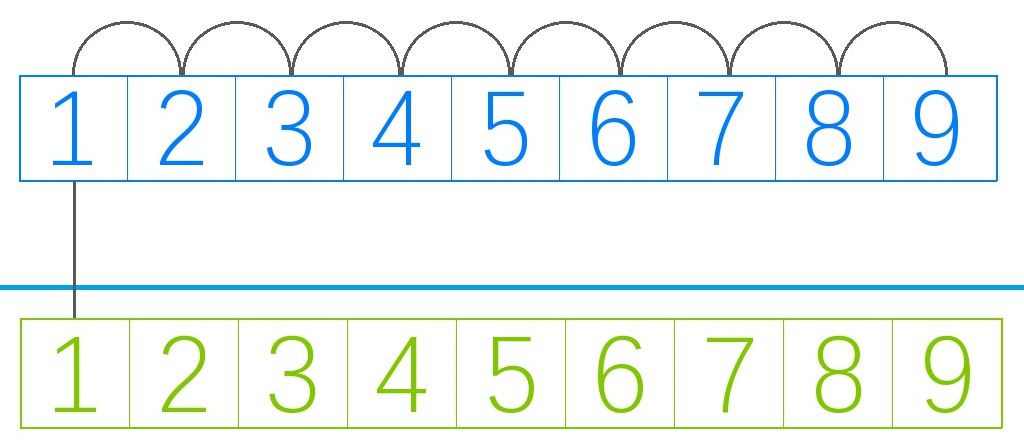
我们知道前缀和：

其中下面的为原数组 \(a\)，上面的为前缀和

\[S_i=\sum_{j=1}^i a_j=\begin{cases}a_1 & i=1\\S_{i-1}+a_i&i>1\end{cases} \]

我们知道，前缀和可以维护静态区间和，显然 \(\sum\limits_{i=l}^r a_i=S_r-S_{l-1}\) .

但是如果要维护单点修改，区间求和的话，每次修改就要把它后面的每个前缀和修改，复杂度 \(O(n)\) .

我们考虑将前缀和变为树形结构，使得其修改时只需要修改其祖先节点即可。

2. 树状数组

我们定义

\[C_i=\sum_{j=i-2^k+1}^i a_i \]

其中 \(k\) 为 \(i\) 二进制末尾 \(0\) 的个数 .

我们可以发现：

\(i\)	二进制表示	\(k\)	\(2^k\)	\(i-2^k+1\)	区间	\(C_i\)
\(1\)	\((1)_2\)	\(0\)	\(2^0=1\)	\(1\)	\([1,1]\)	\(a_1\)
\(2\)	\((10)_2\)	\(1\)	\(2^1=2\)	\(1\)	\([1,2]\)	\(C_1+a_2\)
\(3\)	\((11)_2\)	\(0\)	\(2^0=1\)	\(3\)	\([3,3]\)	\(a_3\)
\(4\)	\((100)_2\)	\(2\)	\(2^2=4\)	\(1\)	\([1,4]\)	\(C_2+C_3+a_4\)
\(5\)	\((101)_2\)	\(0\)	\(2^0=1\)	\(5\)	\([5,5]\)	\(a_5\)
\(6\)	\((110)_2\)	\(1\)	\(2^1=2\)	\(5\)	\([5,6]\)	\(C_5+a_6\)
\(\cdots\)	\(\cdots\)	\(\cdots\)	\(\cdots\)	\(\cdots\)	\(\cdots\)	\(\cdots\)

表的最后一列表示了它们的递推关系。

大概样子是这样的：

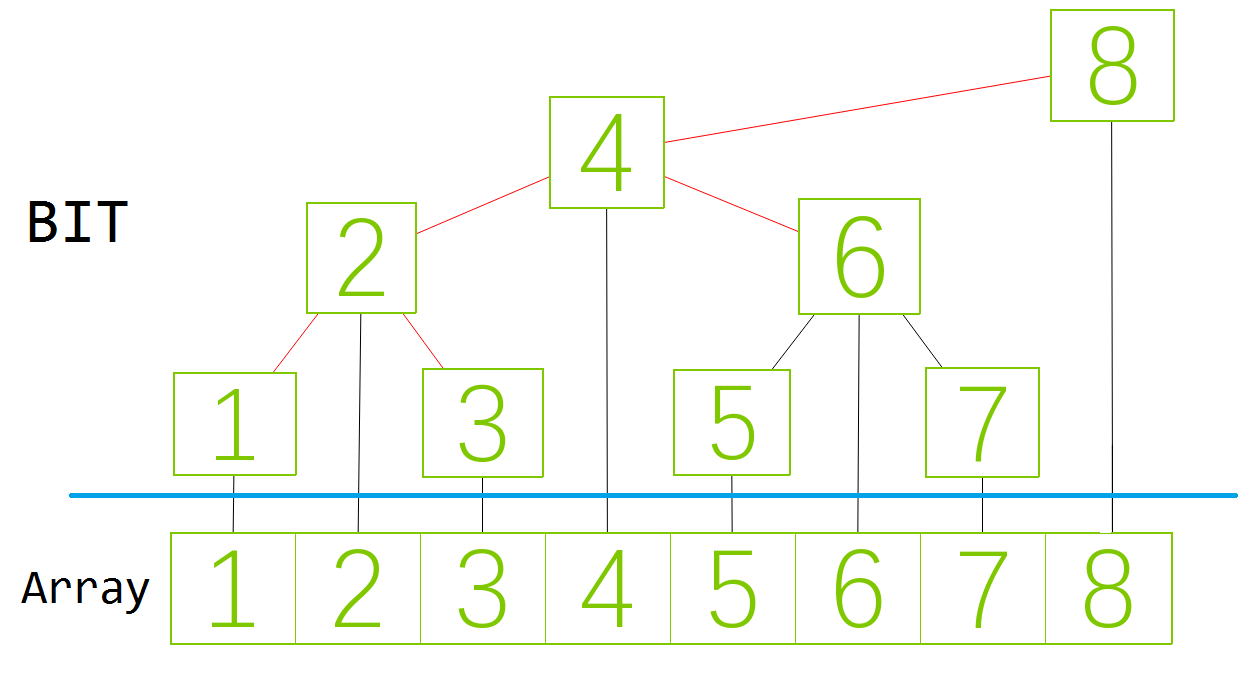
其中下面是数组 \(a\)，上面是数组 \(C\) .

不难发现，\(k\) 就是这棵树的树高，显然二进制中末尾 \(0\) 的个数不会超过这个二进制的位数，所以树高是 \(O(\log n)\) 的。

我们试着计算 \(\sum\limits_{i=1}^n a_i\)（前缀和）：

• \(1\) 到 \(6\) 求和：\(a_1+a_2+\cdots +a_6=C_6+C_4=C_{(110)_2}+C_{(100)_2}\)，\(6=(110)_2\) .
• \(1\) 到 \(7\) 求和：\(a_1+a_2+\cdots +a_7=C_7+C_6+C_4=C_{(111)_2}+C_{(110)_2}+C_{(100)_2}\)，\(7=(111)_2\) .

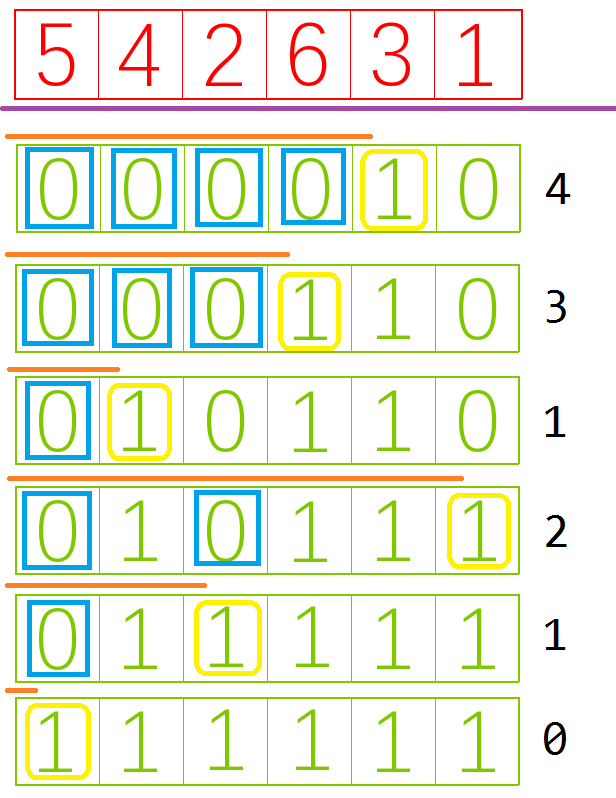
显然这个 \(C\) 的下标是每次 \(n\) 去掉末尾一个 \(1\) 后的值，这个值就是 n&(n-1) .

现在我们考虑 \(2^k\) 怎么计算。

先给结论：i&-i。

我们来验证一下：

• 显然当 \(x=0\) 时命题成立。
• 当 \(x\) 为奇数时：最后一位为 \(1\)，取反加 \(1\) 没有进位，故 \(x\) 和 \(-x\) 除最后一位外前面的位正好相反，所以结果为 \(1\)，正确。
• 当 \(x\) 为二的次幂时：令 \(x=2^m\)，\(m\) 为整数。
  显然 \(x\) 的二进制表示中只有最高位位是 \(1\)，故 \(x\) 取反加 \(1\) 后，从右到左第有 \(m\) 个 \(0\)，第 \(m+1\) 位及其左边全是 \(1\)。这样结果是 \(x\)，正确。
• 当 \(x\) 为偶数但不为二的次幂时：令 \(x=y\times 2^k\)，其中 \(y\) 为奇数（即其最低位为 \(1\)）。
  这时，\(x\) 的二进制表示最右边有 \(k\) 个 \(0\)，从右往左第 \(k+1\) 位为 \(1\)。当对 \(x\) 取反时，最右边的 \(k\) 个 \(0\) 变成 \(1\)，第 \(k+1\) 位变为 \(0\)；再加 \(1\)，最右边的 \(k\) 位就又变成了 \(0\)，第 \(k+1\) 位因为进位的关系变成了 \(1\)。左边的位因为没有进位，正好和 \(x\) 原来对应的位上的值相反。二者按位与得到第 \(k+1\) 位上为 \(1\)，左边右边都为 \(0\) 的二进制数，即 \(2^k\)，正确。

Q.E.D.

这个 \(2^k\) 其实也是 \(\rm lowbit\) 运算，即 \(2^k=\operatorname{lowbit}(i)\)，显然 \(C\) 的下标也是 \(n-\operatorname{lowbit}(n)\).

动图（来自 VisuAlgo）

代码：

const int N=500005;
int n,m,a[N];
template<typename T>
struct BIT // 树状数组
{
private:
	T s[N];
	inline T lowbit(T x){return x&-x;}
public:
	inline void build(T* arrb,T* arre){for (int i=0;arrb+i<arre;i++) add(i+1,*(arrb+i));} // 建立树状数组相当于 n 个单点修改
	inline void build(T* arr,int end){for (int i=0;i<end;i++) add(i+1,arr[i]);}
	inline void build(T* arr,int beg,int end){for (int i=beg;i<end;i++) add(i-beg+1,arr[i]);}
	inline T query(T x) // 下面的这些操作的注释在「不封装的写法」里有
	{
		T ans=0;
		while (x){ans+=s[x]; x-=lowbit(x);}
		return ans;
	}
	inline T query(T l,T r){return query(r)-query(l-1);}
	inline void add(int x,T now){if (x) while (x<=n){s[x]+=now; x+=lowbit(x);}}
};

// 不封装的写法：

const int N=500500;
typedef long long ll;
ll s[N];
int n,m;
inline int lowbit(int x){return x&(-x);} // lowbit
inline ll query(int x) // 区间查询，查询 1~x 的和，查询 l~r 的和时可以按照前缀和的方式减
{
	int ans=0;
	while (x){ans+=s[x]; x-=lowbit(x);} // ans 累加，x 每次去掉末位的 1
	return ans;
}
inline void add(int x,ll now){while (x<=n){s[x]+=now; x+=lowbit(x);}} // x 每次加上末位的 1 就可以寻找祖先了

这里 query 函数和 add 函数的时间复杂度均为 \(O(\log n)\) .

2. 树状数组普通应用

1. 单点修改单点查询

这个直接用普通数组就行（（（（（（（（

2. 单点加区间求和

• 洛谷 P3374 【模板】树状数组 1
• loj #130. 树状数组 1 ：单点修改，区间查询
  上面讲过了

3. 区间加单点查询

• 洛谷 P3368 【模板】树状数组 2
• loj #131. 树状数组 2 ：区间修改，单点查询
  对 \([l,r]\) 的区间修改时在树状数组的第 \(l\) 个位置加这个数，在 \(r+1\) 位置减这个数（差分）。

把这个数组做前缀和，\([l,r]\) 之间会加上这个数，到 \(r+1\) 的时候加减抵消，所以 \([r+1,n]\) 没有影响。

这就把区间修改单点查询变成了两个单点修改加上一个区间查询了。

Code：

BIT<int> s;
void update(int l,int r,int x){s.add(l,x); s.add(r+1,-x);} // 在 l 处加这个数，r+1 处减这个数
int main()
{
    scanf("%d%d",&n,&m);
    for (int i=1;i<=n;i++)
    {
        scanf("%d",a+i);
        s.add(i,a[i]-a[i-1]); // 建立
    } int opt,l,r,k;
    while (m--)
    {
        scanf("%d",&opt);
        if (opt==1){scanf("%d%d%d",&l,&r,&k); update(l,r,k);}
        else scanf("%d",&k),printf("%d\n",s.query(k)); // 查询时查询 1~k 的和即可
    }
    return 0;
}

4. 区间加区间求和

• 洛谷 P3372 【模板】线段树 1
• loj #132. 树状数组 3 ：区间修改，区间查询

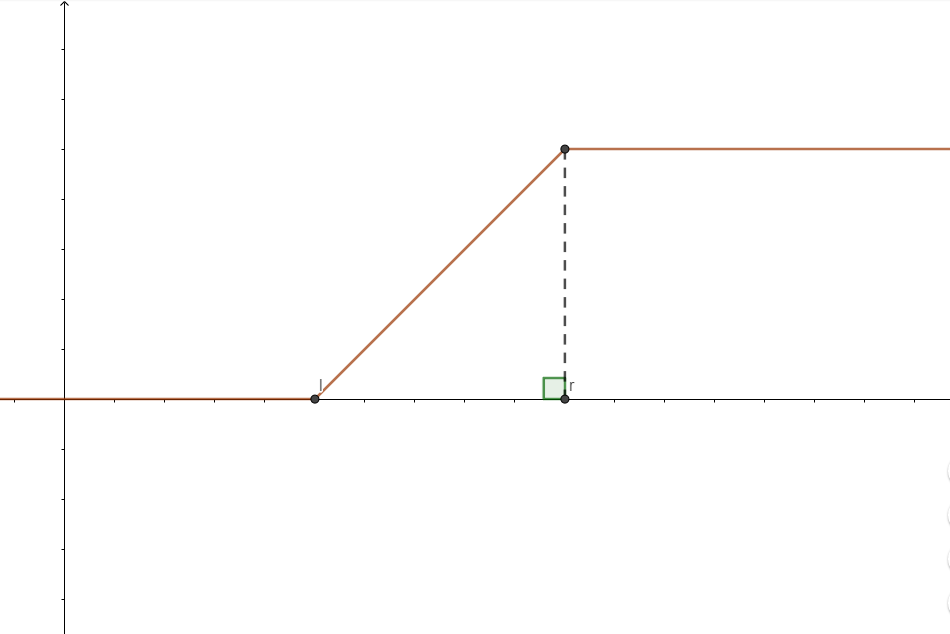
考虑对于一个前缀和做区间加（不妨设是加 \(x\)），它会变成这样：

显然这个新的前缀和如下：

\[S'_i=\begin{cases}S_i & 1\le i< l \\ S_i+(i-l+1)x & l\le i\le r\\ S_i+(r-l+1)x & r<i\le n\end{cases} \]

我们维护两个数组 \(A,B\)，每次区间修改就只需要执行 \(A_l=-x(l-1)\)，\(B_l=x\)，\(A_r=xr\)，\(B_r=-x\)（用差分）

这样 \(S'_i\) 就是 \(\sum\limits_{j=1}^iA_j+i\sum\limits_{j=1}^iB_j\) 了。

直接推比较困难，我们可以验证一下它的正确性：

• \(1\le i<l\)：显然正确
• \(l\le i\le r\)：此时

\[\begin{aligned}\sum\limits_{j=1}^iA_j+i\sum\limits_{j=1}^iB_j&=-x(l-1)+xi\\&=(i-l+1)x\end{aligned} \]

• \(r< i\le n\)：此时

\[\begin{aligned}\sum\limits_{j=1}^iA_j+i\sum\limits_{j=1}^iB_j&=xr-x(l-1)+(-x+x)i\\&=(r-l+1)x\end{aligned} \]

故正确。

Code：

BIT<ll> A,B; // 不开 long long 见祖宗
void update(int l,int r,int x){A.add(l,x*(1-l)); A.add(r+1,x*r); B.add(l,x); B.add(r+1,-x);}
int main()
{
    scanf("%d%d",&n,&m);
    for (int i=1;i<=n;i++){scanf("%d",a+i); A.add(i,a[i]);}
    int opt,l,r,k;
    while (m--)
    {
        scanf("%d",&opt);
        if (opt==1){scanf("%d%d%d",&l,&r,&k); update(l,r,k);}
        else 
        {
            scanf("%d%d",&l,&r);
            ll ans=A.query(r)+r*B.query(r)-A.query(l-1)-B.query(l-1)*(l-1); // 计算时的式子比较长
            printf("%lld\n",ans);
        }
    }
    return 0;
}

5. 树状数组求逆序对

• 洛谷 P1908 逆序对

首先先把数都丢到桶里，然后一个个从小到大加入树状数组，每次的前缀和就是比它小的数的数量，用 \(i\) 减一下就是逆序对的数量，累加一下即可。

Code：

ll ans;
void init()
{
	for (int i=0;i<n;i++) tmp[i]=a[i];
	sort(tmp,tmp+n); int c=unique(tmp,tmp+n)-tmp;
	for (int i=0;i<n;i++)
		a[i]=lower_bound(tmp,tmp+c,a[i])-tmp+1;
}
int main()
{
	scanf("%d",&n);
	for (int i=0;i<n;i++) scanf("%d",a+i); init();
	for (int i=0;i<n;i++) s.add(a[i],1),ans+=i-s.query(a[i]);
	printf("%lld",ans);
	return 0;
}

3. 优化

1. \(O(n)\) 建树

树状数组的 \(O(n)\) 建树思想简单来说就是把所有 \(j+\operatorname{lowbit}(j)=i\) 的节点 \(c_j\)（\(j<\operatorname{lowbit}(i)\)） 累加到 \(c_i\) 中 .

Code 1（填表法）：

for (int i=1;i<=n;i++)
{
	scanf("%lld",s+i);
	for (int j=1;j<lowbit(i);j*=2) s[i]+=s[i-j];
}

Code2（刷表法）:

for (int i=1;i<=n;i++)
{
    scanf("%lld",&x); s[i]+=x;
    if (i+lowbit(i)<=n) s[i+lowbit(i)]+=s[i];
}

2. 时间戳优化

对付多组数据很常见的技巧。

如果每次输入新数据时都暴力清空树状数组，就可能会造成超时。

因此使用 \(tag\) 标记，存储当前节点上次使用时间（即最近一次是被第几组数据使用）。每次操作时判断这个位置 \(tag\) 中的时间和当前时间是否相同，就可以判断这个位置应该是 \(0\) 还是数组内的值。

3. 查询优化

树状数组查询区间和的方式是求前缀和，然后减，但是这种方法有些被重复计算了，并且和答案还没影响（因为被消掉了）。

稍微改改 query 即可优化：

int query(int l,int r)
{
	l--; int sum=0;
	while (r>l) sum+=a[r],r-=lowbit(r);
	while (l>r) sum-=a[l],l-=lowbit(l);
	return sum;
}

4. k 叉树状数组

1. 整数叉树状数组

比对：

\(\quad\)	二叉树状数组	三叉树状数组	\(\cdots\)	\(k\) 叉树状数组
单点修改	\(\log_2 n\)	\(\log_3 n\)	\(\cdots\)	\(\log_k n\)
区间查询	\(\log_2n\)	\(2\log_3n\)	\(\cdots\)	\((k-1)\log_k n\)

我们看出，三叉树状数组的查询理论上比二叉树状数组慢，但修改更快一些。而在实际使用时，除了修改与查询一样多的题目，更多的是查询比修改多（毕竟只有查询有输出）。

所以，如果有 \(k\) 叉树状数组（\(k<2\)），那么就能做到查询比二叉树状数组快。

这样，只能考虑 \(k\) 不为整数的情况。

2. \(\phi\) 叉树状数组

区间树在某种意义上也可以构造出这样的结构：

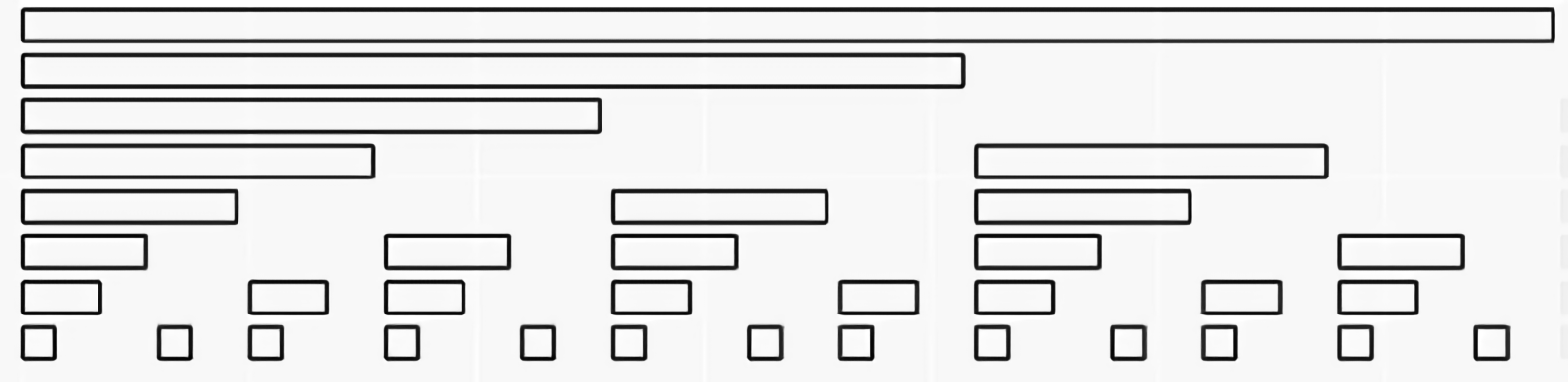
这就是一棵以黄金分割（斐波那契数列）为基础的树状数组，\(k=\phi=0.618\cdots\) .

虽然这样的树层数增多，影响修改的效率，但如果查询比修改多，这样的树状数组就能拥有理论上更小的常数。

3. 总结

我们也得到了这样的结论：

对于 \(k\) 叉树状数组，\(k\) 越大，查询越慢，修改越快；\(k\) 越小，查询越快，修改越慢。

当然，实际应用中还是最好用二叉树状数组，由于有位运算，所以二叉树状数组的代码量最少，而且实际常数往往更小。

而其他树状数组只能通过预处理一个数组来实现它们的类 lowbit 运算。

我们也同时发现树状数组和很多数据结构都有联系，其他很多数据结构实质是树状数组的变体，或树状数组是一些其他数据结构的结合：

• \(k=n\)：暴力
• \(k=\sqrt n\)：分块
• \(k=1\)：普通前缀和

4. 树状数组中级应用

1. 单点加区间最值

先建树：

for (int i=1;i<=n;i++)
{
	cin>>a[i]; int pos=i;
	while (pos<=n) c[pos]=max(c[pos],a[i]),pos+=lowbit(pos);
}

树状数组相当于一个前缀和，求和时可以用 \(S_r-S_{l-1}\)，但是最值没有这种减法的性质，所以这种建树每次查询前都必须初始化，时间复杂度难以接受，让我们换一种写法试一试：

for (int i=1;i<=n;i++)
{
	cin>>c[i]; int t=lowbit(i);
	for (int j=1;j<t;j*=2) c[i]=max(c[i],c[i-j]);
}

嗯，\(O(n)\) 建树的写法。

现在更新完某个数，之前的元素的值都是正确的了。

换了一种建树的方式就是为了维护 c 数组的正确性，修改同样也要保证 c 数组的正确性，那么在更新父亲节点时，我们就需要查询它所有的儿子节点，代码如下：

void add(int pos,int x)
{
	a[pos]=x;
	while (pos<=n)
	{
		c[pos]=x; int t=lowbit(pos); 
		for (int j=1;j<t;j<<=1) c[pos]=max(c[pos],c[pos-j]);
		pos+=lowbit(pos);
	}
}

这个 add 的时间复杂度是 \(O(\log^2 n)\) 的 .

查询操作：

假设当前查询的区间是 \([l,r]\)，那么我们从 \(r\) 到 \(l\) 对每一个 \(c\) 数组的元素所控制的叶子节点进行判断。假设现在进行到了第 \(i\) 项，那么显然易得：该数控制的 \(a\) 数组的元素是 \([i-\operatorname{lowbit}(i)+1,i]\) . 设 \(L=i-\operatorname{lowbit}(i)+1,R=i\)。如果 \(l\le L\le r\) 那么就将 \(c_L\) 加入最值的判断中，接着 \(L\gets L-1\) \(\cdots\)，否则的话就只对第 \(R\) 个元素加入，然后 \(R\gets R-1\) \(\cdots\)，代码如下：

int query(int l,int r)
{
	int ans=a[r];
	while (true)
	{
		ans=max(ans,a[r]); if (r==l) break; --r;
		while (r-l>=lowbit(r)) ans=max(ans,c[r]),r-=lowbit(r);
	}
	return ans;
}

这个 query 也是 \(O(\log^2 n)\) 的。

2. 静态区间最值

见 https://www.zhihu.com/question/27919834/answer/39925959

3. 二维树状数组

加一维即可，EZ

5. 树状数组高级应用

1. 树状数组加 lazytag

毒瘤，咕咕咕

2. 可持久化树状数组

毒瘤，咕咕咕

3. 树状数组实现 BST 的功能

2022.1.18，更新了 .

和权值线段树做法本质相同吧 .

upd 2022/2/22. 好像不太一样

Reference

• 树状数组详解 - Xenny
• 浅谈树状数组的优化及拓展 - 逆流之时
• 可以代替线段树的树状数组?——树状数组进阶(1) - Chanis
• 可以代替平衡树的树状数组?——树状数组进阶(2) - Chanis
• 树状数组 - OI Wiki