Programming Differential Privacy 阅读参考（part 3）

Programming Differential Privacy 阅读参考（part 3）

Programming Differential Privacy 链接

ch6 敏感度

在第四章的拉普拉斯机制部分，提到使查询满足差分隐私所需的噪声大小，取决于查询的敏感度。简单地说，函数的敏感度反映了当输入变化时，函数输出的变化量

全局敏感度（Global Sensitivity）：给定一个将数据集（D）映射为实数的函数 f : D->R，f 的全局敏感度GS为

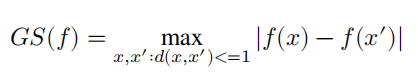
• d(x,x')：数据集x和x'之间的距离，如果两个数据集之间的距离<=1，就认为它们是相邻/临近的（neighbors）

全局敏感度的定义说明，对于任意两个相邻数据集x和x'，函数f(x)和f(x')的输出最多相差GS(f)。这个定义与具体的数据集无关（对任意的neighboring x and x' 都成立），所以称为“全局”敏感度

距离

有很多方法可以度量距离d(x,x')，直观看来，如果两个数据集之间只有一个个体的数据不同，那么距离应为1（即为相邻数据集）。在某些场景下，这个思想很容易用公式表达（e.g. 人口普查，每个人对应一条数据），但另一些场景下（e.g. 位置轨迹，社交网络等）难以用数学语言表达

按行存储（containing rows）的数据集，通常把距离定义为，两个数据集之间不相同的行数。用数学语言表示，这个距离度量方法可以定义为，两个数据集的对称差（Symmetric Difference）：

d(x,x')=|x-x'∪x'-x|

• 关于对称差的概念，可参考对称差集

可见，如果x'是由x增加/删除一行构造的，则d(x,x')=1；如果x'是由x修改一行构造的，则d(x,x')=2

这种对距离的特殊定义，通常形成无界差分隐私（unbounded differential privacy）；也存在其他的距离定义，包括有界差分隐私（bounded differential privacy）认为修改数据集中的一行数据可构成相邻数据集

计算敏感度

对于实数域上的简单函数，函数的敏感性是显而易见的，直接观察x变化时，f(x)的变化情况即可。所以对于将数据集映射到实数域的函数，我们都可以进行类似的分析

计数查询（counting queries）

计数查询（SQL中的COUNT）计算数据集中，满足特定属性的行数

一般来说，计数查询的敏感度总是为1，因为向数据集中添加一行数据，最多使查询的输出结果增加1（即当新增行满足特定属性时），如果不满足，输出结果不变

求和查询（summation queries）

求和查询（SQL中的SUM）对数据集中，行的属性值进行求和

计算求和查询的敏感度比计数查询复杂，因为查询的敏感度取决于我们添加的具体数据是什么（e.g. 对年龄进行求和，敏感度取决于我们增加的一行中，年龄是多少）。对于年龄属性，我们可能找到合理的上界，但对一些其他属性（e.g. 收入等）很难找到一个合理的上界，使得任何添加的行都不会违背这个敏感度

一般来说，当要求和的属性值没有上下界时，求和查询具有无界敏感度（unbounded sensitivity），当上下界存在时，求和查询的敏感度等于上下界的差

均值查询（average queries）

均值查询（SQL中的AVG）计算指定列中，属性值的平均值

使用DP回答均值查询，可以直接将其重新定义为两个查询：求和查询除以计数查询（e.g. 平均年龄=年龄和/行数）。获得这两个查询的noisy answers之后，即可得到满足差分隐私的均值，其总隐私消耗可以用串行组合性计算

裁剪（clipping）

使用拉普拉斯机制无法以DP直接回答具有无界敏感度的查询，但我们可以通过裁剪，将其转换为等价的有界敏感度查询

裁剪的基本思想是，强制设置属性值的上界和下界（e.g. 将125岁以上的年龄都裁剪为125岁）

裁剪技术的主要挑战是确定属性值的上界和下界，不同属性的难度不同。同时，还要在裁剪造成的信息损失量和所需噪声的大小之间进行权衡：裁剪的上下界越接近，敏感度越低，所需的噪声越小，但过分裁剪会从数据中移除很多信息，给准确度带来的损失超过（降低噪声带来的）准确度收益

通过直接查看数据选择裁剪边界的方法并不满足差分隐私的要求，因为边界本身可能泄露数据的信息。所以我们可以应用差分隐私查询，估计选取的边界是否恰当

ch7 近似差分隐私

近似差分隐私（Approximate Differential Privacy）也称(ε,δ)-DP，定义为：Pr[F(x)=S] <= e^εPr[F(x')=S] + δ

• 隐私参数δ：表示失败概率
• 我们有1-δ的概率获得纯粹差分隐私（pure differential privacy）的保护，即Pr[F(x)=S] / Pr[F(x')=S] <= e^ε
• 通常要求δ是一个很小的数，一般小于1/n²，其中n是数据库的大小
• 失败的时候并不会造成整个数据库泄露的严重后果，实际上是温和地（gracefully）失败

近似差分隐私的性质

近似差分隐私与纯粹的ε-DP有相似的性质，包括串行组合、并行组合、后处理，其中串行组合性与纯粹的ε-DP有一些不同，需要对ε和δ进行相加：

• 如果F₁ (x)满足(ε₁,δ₁)-DP，F₂ (x)满足(ε₂,δ₂)-DP
• 则同时发布两个结果的机制G(x)=(F₁ (x), F₂ (x))满足(ε₁ +ε₂ , δ₁ +δ₂)-DP

高斯机制

高斯机制添加的是高斯噪声，无法满足纯粹的ε-DP，但可以满足(ε,δ)-DP

根据高斯机制，对一个返回数值的函数f(x)，按下述方法定义的F(x)满足(ε,δ)-差分隐私：

F(x) = f(x) + N(σ²)，其中σ² = 2s²log(1.25/δ) / ε²

• s是f的敏感度
• N(σ²)表示均值为0，方差为σ²的高斯（正态）分布的采样结果
• log x表示自然对数，即ln x

当ε相同时，高斯机制的概率密度函数图像，看上去比拉普拉斯机制的图像更平缓， 更有可能得到远离真实值的输出结果

向量值函数及其敏感度

实值函数（real-valued functions）：输出总是一个实数的函数，形式为f : D->R

向量值函数（vector-valued functions）：输出为实数向量的函数，形式为f : D->R^k

拉普拉斯机制和高斯机制都可以扩展到向量值函数

向量差：计算对应元素的差，两个长度为k的向量差是一个长度为k的新向量（e.g. (5,8,4)-(3,5,1)=(2,3,3)）

向量值函数的敏感度：f是向量值函数，向量f(x)-f(x')的标量长度，就是f的敏感度

计算向量的标量长度：

• L1范数（L1 norm）：向量中各个元素的和。二维空间中，两个向量之差的L1范数就是曼哈顿距离
• L2范数（L2 norm）：向量中各个元素平方和的平方根。二维空间中，两个向量之差的L2范数就是欧氏距离
• L2范数总是小于等于L1范数

对一个向量值函数f：

• L1敏感度：GS(f) = max_d(x,x')<=1 ||f(x)-f(x')||₁ ，L1敏感度等于向量中各个元素敏感度的和
• L2敏感度：GS(f) = max_d(x,x')<=1 ||f(x)-f(x')||₂
• 对于长向量，L2敏感度比L1敏感度低得多

向量值拉普拉斯机制需要使用L1敏感度，而向量值高斯机制既可以使用L1敏感度，也可以使用L2敏感度。这是高斯机制的一个重要优势，对于L2敏感度远小于L1的应用来说，高斯机制可以添加少得多的噪声

对于向量值函数发布的f(x)+(Y₁, Y₂, ... , Y_k)，Y_i 是从拉普拉斯分布/高斯分布中，采样的独立同分布的噪声

灾难机制

灾难机制：F(q,x) = 在0到1之间随机取一个数r，如果r<δ，则返回x，否则返回q(x)+Lap(s/ε)，其中s是q的敏感度

可以看到灾难机制有1-δ的概率满足ε-DP，但同时有δ的概率泄露无噪声的整个数据集x，所以虽然灾难机制满足近似差分隐私的定义，现实中也一般不使用

大部分(ε,δ)-DP机制不会出现类似的灾难性失败，例如高斯机制，只是有δ的概率不满足ε-DP，而满足某个值c下的cε-DP，也就是说，高斯机制会温和地失败，而不会灾难性地失败

高级组合性

(ε,δ)-DP引入了一种DP机制串行组合性的新分析方法，可以进一步降低隐私消耗

k-折叠适应性组合（k-fold adaptive composition）：一系列机制m₁, m₂, ... ,m_k组合起来，每个机制满足

• 适应性：可以根据之前所有机制m₁, m₂, ... ,m_i-1的输出，选择下一个机制m_i
• 组合性：每个机制m_i的输入既包括隐私数据集，也包括previous机制的所有输出

迭代程序（e.g. 循环，递归函数）几乎都是k-折叠适应性组合的实例

高级组合定理：

• 如果k-折叠适应性组合m₁, m₂, ... ,m_k中的每一个机制m_i都满足ε-DP
• 则对任意δ’>=0，整个 k-折叠适应性组合满足 (ε',δ')-DP，其中 ε' = 2ε√2klog(1/δ')

当k<70时，标准的串行组合性比高级组合性得到的总隐私消耗量更小，当k很大时，高级组合性的优势明显

近似差分隐私的高级组合性

如果各个机制满足 (ε,δ)-DP，高级组合定理同样适用。高级组合定理更一般的描述如下：

• 如果k-折叠适应性组合m₁, m₂, ... ,m_k中的每一个机制m_i都满足 (ε,δ)-DP
• 则对任意δ’>=0，整个 k-折叠适应性组合满足 (ε',kδ+δ')-DP，其中 ε' = 2ε√2klog(1/δ')

可以看到与前面的高级组合定理的描述之间，唯一的区别是失败参数（failure parameter），多了一个kδ项，如果组合的机制满足pure ε-DP，那么δ=kδ=0，和前面的描述一致

点击跳转part 4